Assertion: To conserve linear momentum of a system, no force should act on the system.
Reason: If net force on a system is zero, its linear momentum should remain constant.
(a) If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b) If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false but the Reason is true.
The correct Answer is:D
To analyze the assertion and reason provided in the question, we can break it down step by step:
Step 1: Understanding the Assertion
The assertion states: "To conserve linear momentum of a system, no force should act on the system."
- This statement implies that for momentum to be conserved, there should be an absence of any forces acting on the system.
Step 2: Evaluating the Assertion
In reality, momentum can be conserved in a system even if forces are acting on it, as long as the net external force acting on the system is zero.
- For example, consider two bodies connected by a string. Even if gravitational forces are acting on them, if the net external force is zero (like in a closed system where internal forces are balanced), the momentum of the system can still be conserved.
Step 3: Understanding the Reason
The reason states: "If net force on a system is zero, its linear momentum should remain constant."
- This statement is correct. According to Newton's first law of motion, if no net external force acts on a system, the momentum of that system remains constant.
Step 4: Conclusion
Based on the evaluation:
- The assertion is false because it incorrectly states that no forces should act on the system for momentum to be conserved.
- The reason is true because it correctly states that if the net external force is zero, the linear momentum remains constant.
Final Answer
The correct answer to the question is that the assertion is false, but the reason is true.
The assertion states: "To conserve linear momentum of a system, no force should act on the system."
In reality, momentum can be conserved in a system even if forces are acting on it, as long as the net external force acting on the system is zero.
The reason states: "If net force on a system is zero, its linear momentum should remain constant."
Based on the evaluation:
- The assertion is false because it incorrectly states that no forces should act on the system for momentum to be conserved.
- The reason is true because it correctly states that if the net external force is zero, the linear momentum remains constant.
The correct answer to the question is that the assertion is false, but the reason is true.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective42videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective32videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Exercise 11.611videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
In net force on a system is zero then
View SolutionThe angular momentum of a system of particles is conserved
View SolutionIf no external force acts on a system
View SolutionIf no external force acts on a system
View SolutionIf net external force acting on the system is zero then
View SolutionIf net force on a system of particles is zero, then match the following.
 View Solution
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
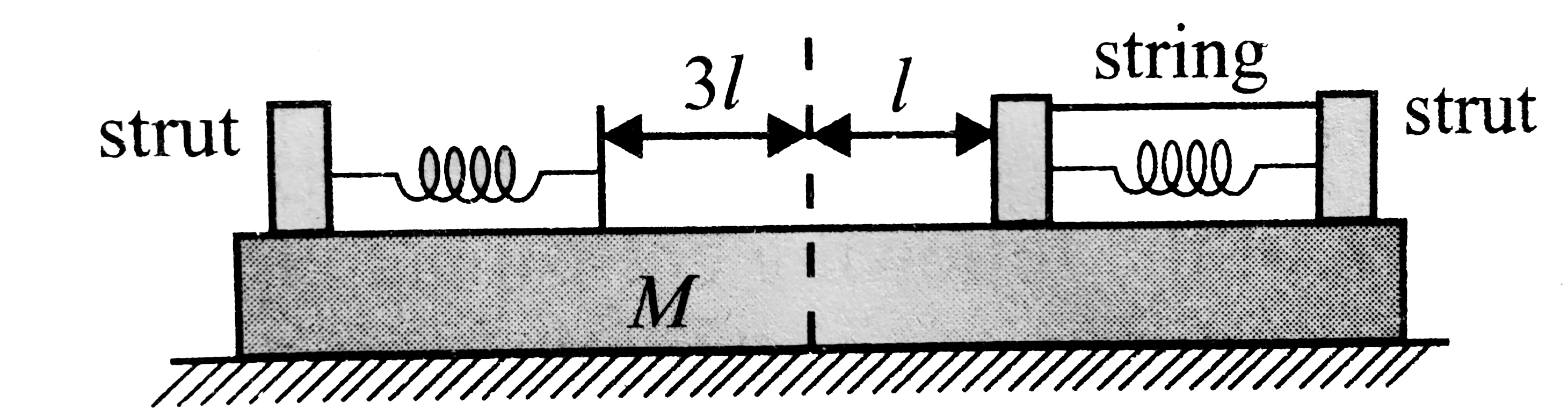
The maximum kinetic energy of the block m isView SolutionStatement 1: Two spheres undergo a perfectly elastic collision. The kinetic energy of system of both spheres is always constant. [There is no external force on system of both spheres].
Statement 2: If net external force on a system is zero, the velocity of centre of mass remains constant.View SolutionWork done by the conservative force on a system is equal to :
View Solution

