Assertion: A ring is rolling without slipping on a rough ground. It strikes elastically with a smooth wall as shown in figure. Ring will stop after some time while travelling in opposite direction.
Reason: After impact net angular momentum about an axis passing through bottommost point and perpendicular to plane of paper is zero.
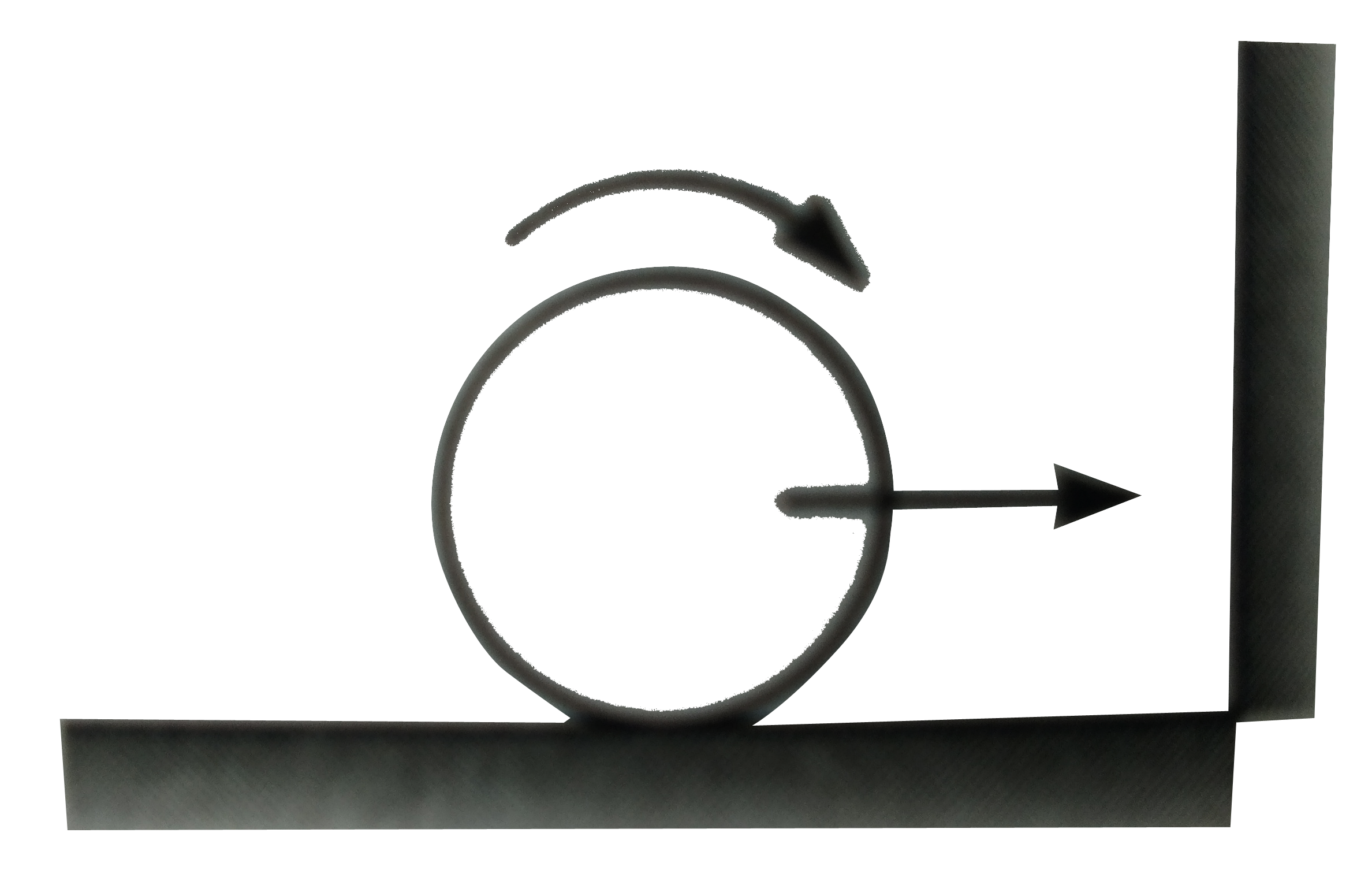
If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
If assertion is true, but the reaction is false.
If assertion is false but the reason is true.
In second figure. Net angular momentum about bottommost axis
L=mvR−ICω
=mvR−(mr2)(vR)
=0
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Objective30videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective32videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.112videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A disc of mass m and radius R is rolling on horizontal ground with linear velocity v. What is the angular momentum of the disc about an axis passing through bottommost point and perpendicular to the plane of motion ?
View SolutionA sphere rolling on a horizontal rough surface collides elastically with a smooth vertical wall, as shown in figure. During collision, angular momentum of the sphere is conserved about ____________. (Any point O on the surface/point of contact P)
View SolutionAssertion: A ball is released on a rough ground in the condition shown in figure. it will start pure rolling after some time towards left side.
Reason: Friction will convert the pure rotational motion of the ball into pure rolling
View SolutionA sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.
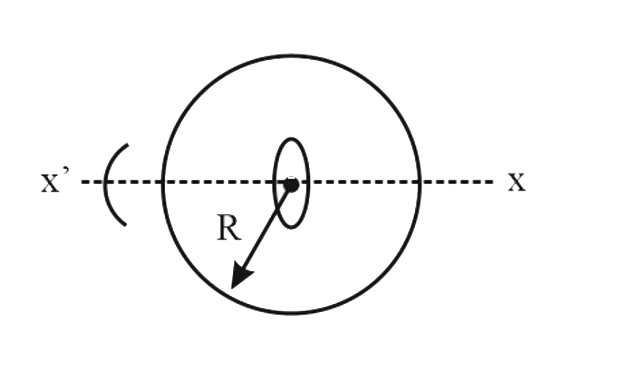
View SolutionA non-conducting ring of radius R having uniformly distributed charge Q starts rotating about x-x' axis passing through diameter with an angular acceleration α, as shown in the figure. Another small conducting ring having radius a(a<<R) is kept fixed at the centre of bigger ring is such a way that axis xx' is passing through its centre and perpendicular to its plane. If the resistance of small ring is r=1Ω , find the induced current in it in ampere.
(Given q=16×102μ0C,R=1m,a=0.1m,α=8rad s−2
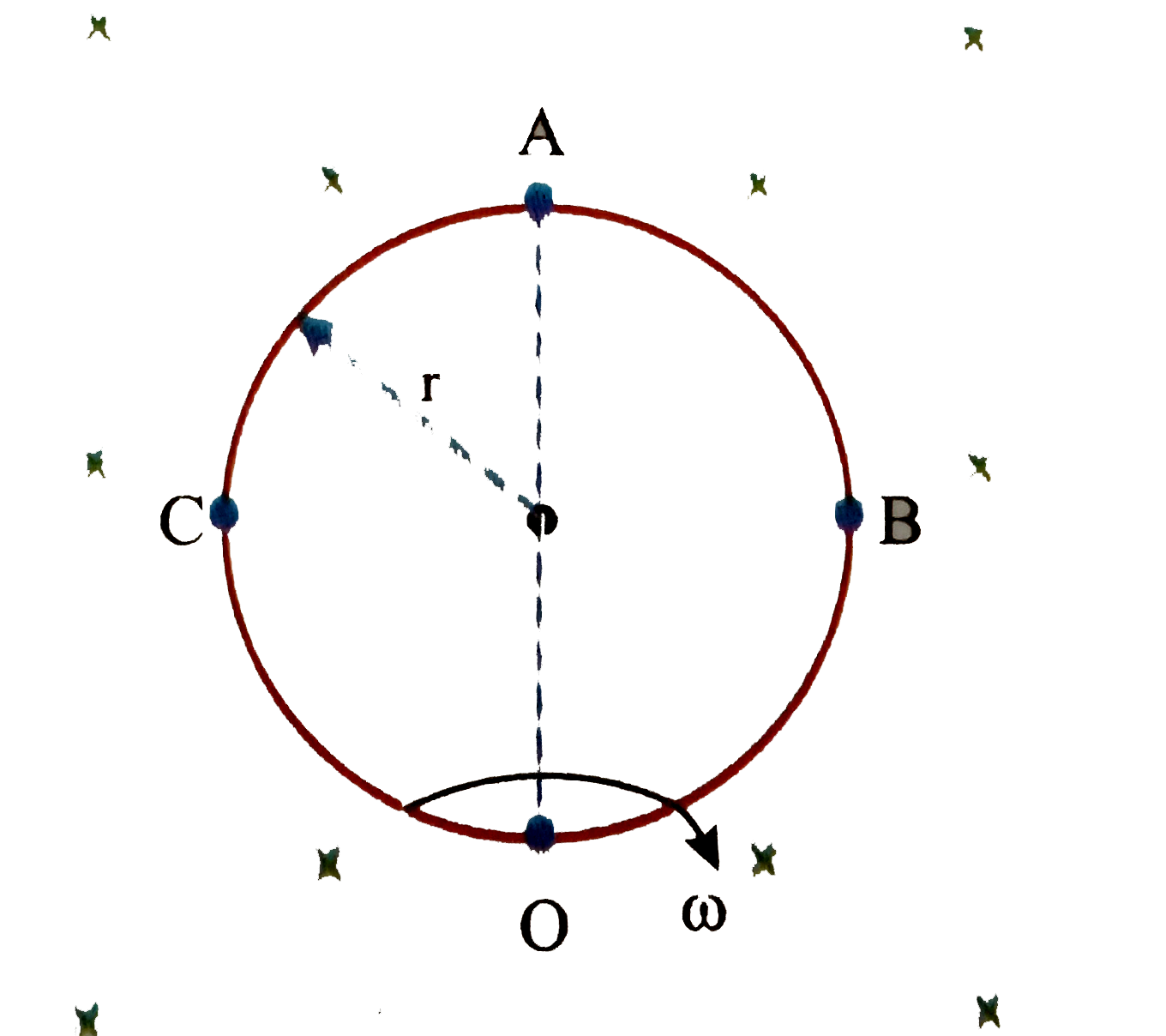
View SolutionIn figure, there is conducting ring having resistance R placed in the plane of paper in a uniform magnetic field B0. If the rings is rotating in the plane of paper about an axis passing through point O and perpendicular to the plane of paper with constant angular speed ω in clockwise direction, then
View SolutionA uniform ring of mass m and radius R is released from top of an inclined plane. The plane makes an angle θ with horizontal. The cofficent of friction between the ring and plane is μ. Initially, the point of contact of ring and plane is P. Angular momentum of ring about an axis passing from point P and perpendicular to plane of motion as a function of time t is
View SolutionA rod of mass m and length 2 R is fixed along te diameter of a ring of same mass m and radius R as shown in figure. The combined body is rolling without slipping along x-axis find the angular momentum about z-axis.
View SolutionAssertion : A uniform disc of radius R is performing impure rolling motion on a rough horizontal plane as shown in figur. After some time the disc comes to rest. It is possible only when v0=ω0R2
Reason : For a body performing pure rolling motion, the angular momentum uis conserved about any point in space.View Solution