Three points A , B and C each of mass m is placed in a line with AB=BC=d. Find the gravitational force on a fourth particle P of the same mass placed at a distance d from particle B on the perpendicular bisector of the line AC.
(√2+1√2)Gm2d2
(√3+1√2)Gm2d2
(√2+1√3)Gm2d2
(√2√5)Gm2d2
The correct Answer is:A, B, D
To solve the problem, we need to find the gravitational force acting on a particle P due to three other particles A, B, and C, each of mass m, placed in a line with distances AB = BC = d. The particle P is located at a distance d from B on the perpendicular bisector of the line AC.
1. Diagram Setup:
- Place points A, B, and C on a horizontal line. Let A be at (-d, 0), B at (0, 0), and C at (d, 0).
- Point P is located at (0, d) on the perpendicular bisector of line AC.
2. Calculate Distances:
- The distance from P to A (denoted as PA) can be calculated using the distance formula:
PA=√(0−(−d))2+(d−0)2=√d2+d2=d√2
- Similarly, the distance from P to C (denoted as PC) is also:
PC=√(0−d)2+(d−0)2=√d2+d2=d√2
- The distance from P to B (denoted as PB) is simply:
PB=d
3. Calculate Gravitational Forces:
- The gravitational force between two masses is given by:
F=Gm1m2r2
- The force exerted on P by A (FA):
FA=Gm2(d√2)2=Gm22d2
- The force exerted on P by B (FB):
FB=Gm2d2
- The force exerted on P by C (FC):
FC=Gm2(d√2)2=Gm22d2
4. Resolve Forces into Components:
- The forces FA and FC will have components along the vertical and horizontal directions. The angles with respect to the vertical are 45 degrees (since P is directly above the midpoint of AC).
- The vertical components of FA and FC are:
FAy=FA⋅cos(45∘)=Gm22d2⋅1√2=Gm22√2d2
FCy=FC⋅cos(45∘)=Gm22d2⋅1√2=Gm22√2d2
- The total vertical force from A and C:
FAy+FCy=Gm22√2d2+Gm22√2d2=Gm2√2d2
5. Total Gravitational Force:
- The total gravitational force acting on P is the sum of the vertical components from A and C plus the force from B:
Fnet=FB+FAy+FCy=Gm2d2+Gm2√2d2
- Factor out Gm2d2:
Fnet=Gm2d2(1+1√2)
Final Answer:
The gravitational force on particle P is:
Fnet=Gm2d2(1+1√2)
- Place points A, B, and C on a horizontal line. Let A be at (-d, 0), B at (0, 0), and C at (d, 0).
- Point P is located at (0, d) on the perpendicular bisector of line AC.
- The distance from P to A (denoted as PA) can be calculated using the distance formula:
PA=√(0−(−d))2+(d−0)2=√d2+d2=d√2
- Similarly, the distance from P to C (denoted as PC) is also:
PC=√(0−d)2+(d−0)2=√d2+d2=d√2
- The distance from P to B (denoted as PB) is simply:
PB=d
- The gravitational force between two masses is given by:
F=Gm1m2r2
- The force exerted on P by A (FA):
FA=Gm2(d√2)2=Gm22d2
- The force exerted on P by B (FB):
FB=Gm2d2
- The force exerted on P by C (FC):
FC=Gm2(d√2)2=Gm22d2
- The forces FA and FC will have components along the vertical and horizontal directions. The angles with respect to the vertical are 45 degrees (since P is directly above the midpoint of AC).
- The vertical components of FA and FC are:
FAy=FA⋅cos(45∘)=Gm22d2⋅1√2=Gm22√2d2
FCy=FC⋅cos(45∘)=Gm22d2⋅1√2=Gm22√2d2
- The total vertical force from A and C:
FAy+FCy=Gm22√2d2+Gm22√2d2=Gm2√2d2
- The total gravitational force acting on P is the sum of the vertical components from A and C plus the force from B:
Fnet=FB+FAy+FCy=Gm2d2+Gm2√2d2
- Factor out Gm2d2:
Fnet=Gm2d2(1+1√2)
The gravitational force on particle P is:
Fnet=Gm2d2(1+1√2)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.2
9 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.3
5 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples
8 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A tunnel is dug along a diameter of the earth. Find the force in on a particle of mass m placed in the tunnel at a distance x from the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the center.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionFour particles having masses, m, 2m, 3m, and 4m are placed at the four corners of a square of edge a. Find the gravitational force acting on a particle of mass m placed at the centre.
View SolutionThree particales P,Q and R are placedd as per given Masses of P,Q and R are √3m√3m and m respectively The gravitational force on a fourth particle 'S' of mass m is equal to
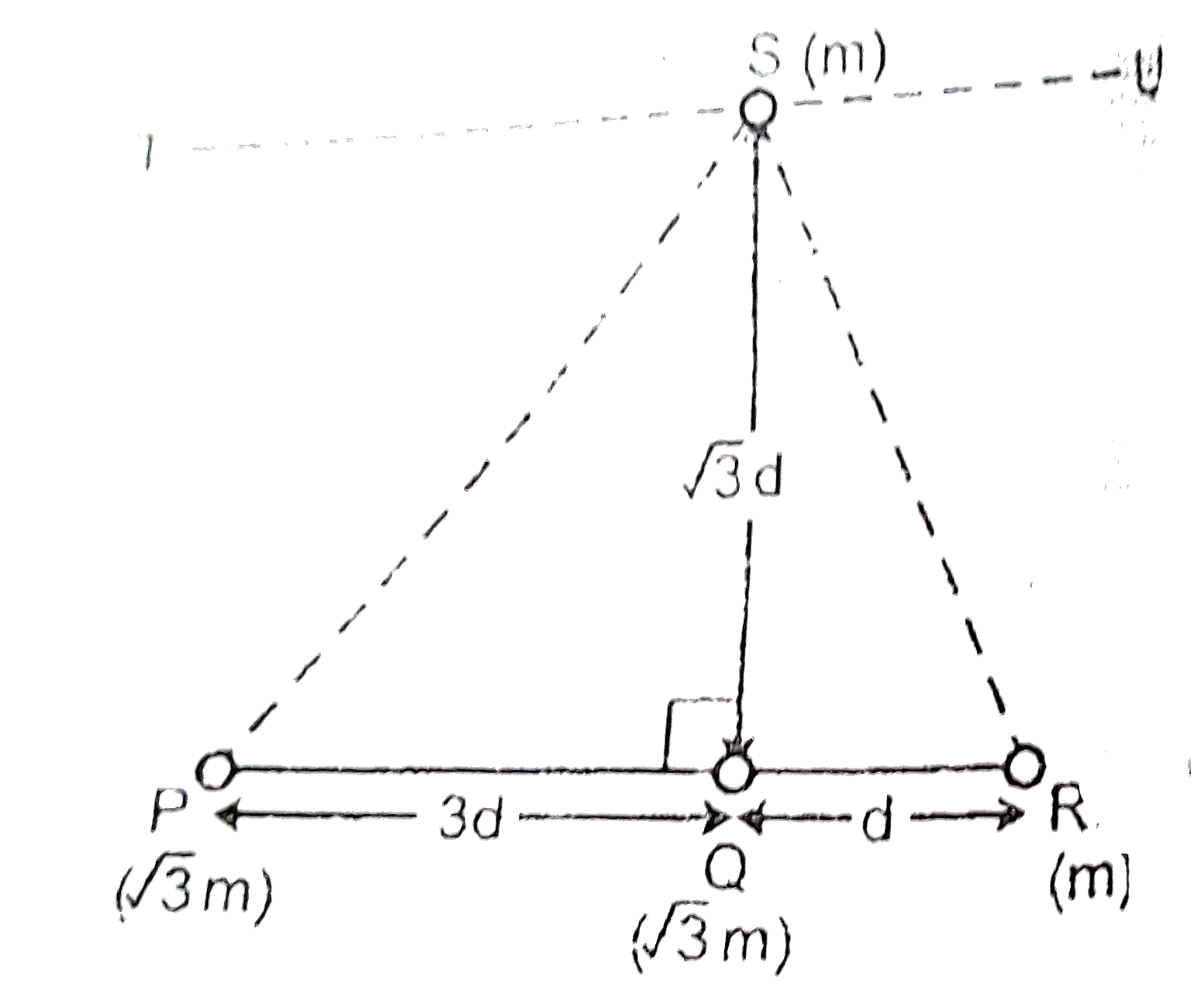 .
.
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree equal masses each of mass 'm' are placed at the three-corner of an equilateral triangle of side 'a'
If a fourth particle of equal mass is placed at the centre of triangle, then net force acting on it, is equal to
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View SolutionThree equal masses each of mass 'm' are palced at the three corners of an equilateral of side a
If a fourth particle of equal mass is placed at the centre of triangle then net force acting on it is equal to .
View Solution