If M is the mass of the earth and R its radius, the radio of the gravitational acceleration and the gravitational constant is
(a)R2M
(b)MR2
(c)MR2
(d)MR
The correct Answer is:B
To find the ratio of gravitational acceleration (g) to the gravitational constant (G), we can follow these steps:
1. Understand the Gravitational Force Equation:
The gravitational force (F) acting on a mass (m) at the surface of the Earth can be expressed using Newton's law of gravitation:
F=GMmR2
where:
- G is the gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth.
2. Relate Force to Gravitational Acceleration:
The gravitational force can also be expressed in terms of mass and acceleration due to gravity (g):
F=mg
3. Set the Two Expressions for Force Equal:
Since both expressions represent the same force, we can set them equal to each other:
mg=GMmR2
4. Cancel Mass (m):
Assuming m≠0, we can divide both sides of the equation by m:
g=GMR2
5. Rearrange to Find the Ratio:
We are interested in the ratio of g to G:
gG=GMR2G
This simplifies to:
gG=MR2
6. Find the Required Ratio:
To express the ratio of G to g, we take the reciprocal:
Gg=R2M
Final Result:
The ratio of the gravitational constant G to the gravitational acceleration g is:
Gg=R2M
The gravitational force (F) acting on a mass (m) at the surface of the Earth can be expressed using Newton's law of gravitation:
F=GMmR2
where:
- G is the gravitational constant,
- M is the mass of the Earth,
- R is the radius of the Earth.
The gravitational force can also be expressed in terms of mass and acceleration due to gravity (g):
F=mg
Since both expressions represent the same force, we can set them equal to each other:
mg=GMmR2
Assuming m≠0, we can divide both sides of the equation by m:
g=GMR2
We are interested in the ratio of g to G:
gG=GMR2G
This simplifies to:
gG=MR2
To express the ratio of G to g, we take the reciprocal:
Gg=R2M
The ratio of the gravitational constant G to the gravitational acceleration g is:
Gg=R2M
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct
22 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Assertion And Reason
11 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
If M be the mass of the earth, R its radius (assumed spherical) and G gravitational constant, then the amount of work that must be done on a body of mass m, so that it completely escapes from the gravity of the earth of the earth is given by
View SolutionThe acceleration due to gravity at a piece depends on the mass of the earth M, radius of the earth R and the gravitational constant G. Derive an expression for g?
View Solution
Knowledge Check
If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
AR2EMEBMER2ECMER2EDMEREThe acceleration due to gravity g and density of the earth ρ are related by which of the following relations? (where G is the gravitational constant and RE is the radius of the earth)
Aρ=4πGRE3gBρ=3g4πGRECρ=3G4πgREDρ=4πgRE3G
The escape velocity of a body from the surface of the earth depends upon (i) the mass of the earth M, (ii) The radius of the eath R, and (iii) the gravitational constnat G. Show that v=k√GMR, using the dimensional analysis.
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is
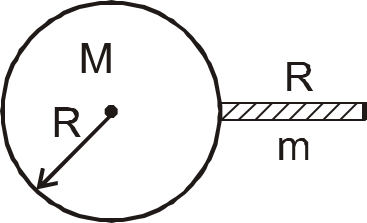
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is

View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is

View SolutionStatement-1: The acceleration of a particle near the earth surface differs slightly from the gravitational acceleration
Statement-2: The earth is not a uniform sphere and because the earth rotates.
View SolutionStatement-1: The acceleration of a particle near the earth surface differs slightly from the gravitational acceleration
Statement-2: The earth is not a uniform sphere and because the earth rotates.
View Solution
