In the figure masses 400kg and 100kg are fixed.
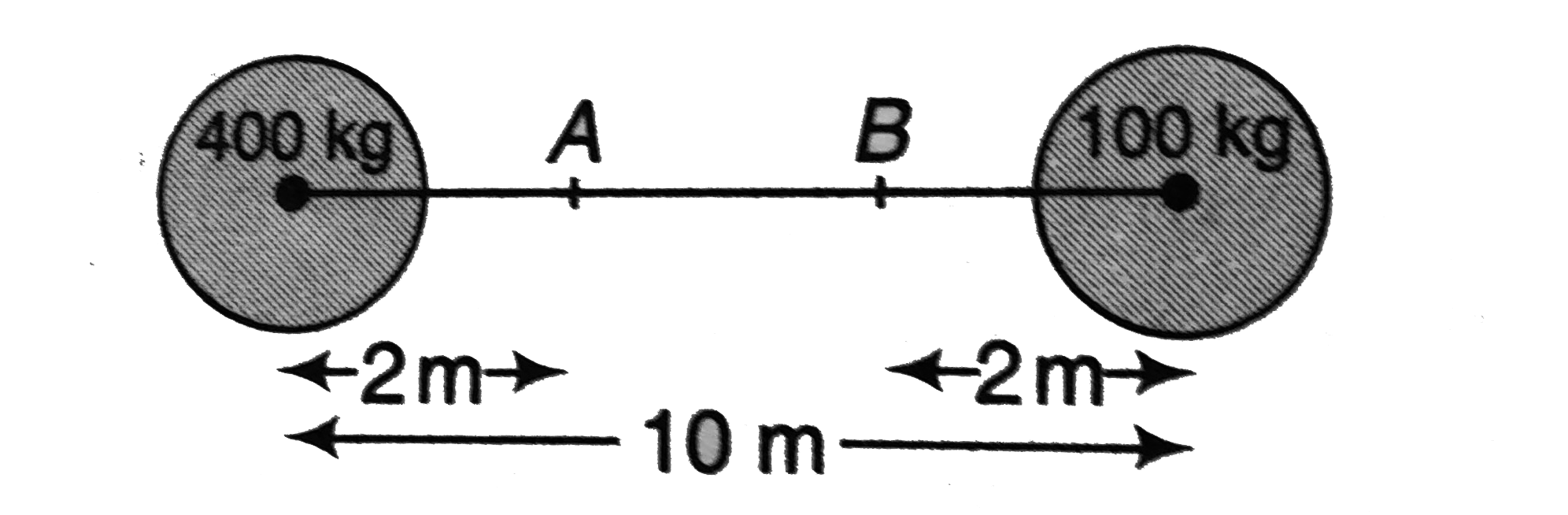
(a) How much work must be done to move a 1kg mass from point A to point B?
(b) What is the minimum kinetic energy with which the 1kg mass must be projected from A to the right to reach the point B?
The correct Answer is:A, B
W=Uf−Ui=UB−UA
=mVB−mVA (V= gravitational potential)
=m(VB−VA)
=(1)[−1002−4008+1008+4002](6.67×10−11)
=7.5×10−9J
(b) First let us find the point (say) c between A and B where field strength due to 400kg and 100kg masses is zero. Let its distance from 400kg is r.
Then, G(400)r2=G(100)(10−r)2
r=203m and (10−r)=103m
So, we have to move the body only from A to C. After that 100kg mass will pull 1kg mass by its own.
∴ Minimum kinetic energy =ΔU=UC−UA
=m(VC−VA)
=(1)[−40020/3−10010/3+1008+4002](6.67×10−11)
=8.17×10−9J
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Single Correct22videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct10videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Single Correct27videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Knowledge Check
- Question 1 - Select One
An object of mass 2 kg has linear momentum magnitude 6 kg⋅m/s. What is this object's kinetic energy?
A3JB6JC9JD12J
A body of mass 50 kg has a momentum of 3000 kg ms−1. Calculate:
The kinetic energy of the body.View SolutionTwo bodies of mass 1kgand2kg have equal momentum. The ratio of their kinetic energies is:
View SolutionA car of mass 1000kg moves from point A to B. If kinetic energy of car at point A is 100KJ and at B is 220Kj. Then find work done by friction force on the car ?
 View Solution
View SolutionA 4 kg mass and a 1 kg mass are moving with equal kinetic energies. The ratio of the magnitudes of their linear momenta is
View SolutionIn the given figure mass of string AB is 2kg. Find tension at A,B and C, where C is the mid point of string.
 View Solution
View SolutionTwo particle of masses 10 kg and 35 kg are connected with four strings at points B and D as shown in fig.

Determine the tension in various segments of the string.View SolutionA block of mass 5 kg is raised from the bottom of the lake to a height of 3m without change in kinetic energy. If the density of the block is 3000kgm−3, then the work done is equal to.
View Solution

