Consider two configurations of a system of three particles of masses m, 2m and 3m. The work done by gravity in changing the configuration of the system from figure (i) to figure (ii) is 
(a)zero
(b)6Gm2a{1+1√2}
(c)6Gm2a{1−1√2}
(d)6Gm2a{2−1√2}
The correct Answer is:C
W=−ΔU=Ui−Uf
=−Gmma[{(1)(2)1+(1)(3)1+(2)(3)√2}]
−{(1×2)1+(1×3)1+(2×3)1}]
=6GM2a(1−1√2)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Knowledge Check
The centre of mass of a system of two particle of masses m1andm2 is at a distance d1 from mass m1 and at a distance d2 from mass m2 such that.
Ad1d2=m2m1Bd1d2=m1m2Cd1d2=m1m1+m2Dd1d2=m2m1+m2
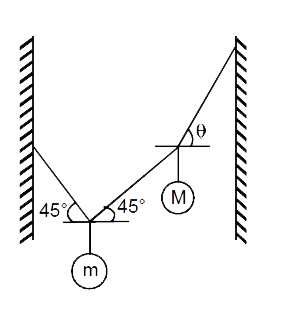
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View SolutionConsider the process on a system as shown in the figure. During the process, the work done by the system

View SolutionThe gravitational potential energy of an isolated system of three particles, each of mass m, at the three corners of an equilateral triangle of side l is
View SolutionThree particles, two with mass m and one with mass M, might be arranged in any of Rank the configuration according of the gravitational force on M, least to greatest.

View SolutionCalculate the position of centre of mass of a system consisting of two particles of masses m_1 and m_2 separated by a distance L apar, from m_1?
View SolutionA particle of mass 1kg is placed at a distance of 4m from the centre and on the axis of a uniform ring mass 5kg and radius 3m. The work done to increase the distance of the particle from 4m to 3√3m is
View SolutionA particle of mass 100g is thrown vertically upwards with a speed of 5m/s. The work done by the force of gravity during the time the particle goes up is
View Solution

 ,
,