Assertion : Time taken by a particle in SHM to move from x=A to x=√3A2 is same as the time taken by the particle to move from x=√3A2 to x=A2.
Reason : Corresponding angles rotated is the reference circle are same in the given time intervals.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.
(c)If Assertion is true, but the Reason is false.
(d)If Assertion is false but the Reason is true.
The correct Answer is:A
To solve the problem, we need to analyze the assertion and reason given in the question step by step.
1. Understanding the Positions:
- We have a particle in Simple Harmonic Motion (SHM) with maximum displacement (amplitude) A.
- The particle moves from x=A to x=√3A2 and then from x=√3A2 to x=A2.
2. Finding Angles:
- For the position x=A, the angle θ1 corresponding to this position is 0∘ (since it is at maximum displacement).
- For the position x=√3A2:
cos(θ1)=xA=√3A/2A=√32⟹θ1=30∘
- For the position x=A2:
cos(θ2)=xA=A/2A=12⟹θ2=60∘
3. Calculating the Angle Covered:
- The angle covered when moving from x=A to x=√3A2 is:
Δθ1=θ1−0=30∘
- The angle covered when moving from x=√3A2 to x=A2 is:
Δθ2=θ2−θ1=60∘−30∘=30∘
4. Time Calculation:
- The total angle in one complete cycle (one period T) is 360∘.
- The time taken to cover 30∘ is:
t=30∘360∘×T=112T
- Thus, the time taken for both intervals is the same, 112T.
5. Conclusion:
- The assertion states that the time taken to move from x=A to x=√3A2 is the same as the time taken to move from x=√3A2 to x=A2, which we found to be true.
- The reason states that the corresponding angles rotated in the reference circle are the same, which is also true.
Final Answer:
Both the assertion and reason are correct.
---
- We have a particle in Simple Harmonic Motion (SHM) with maximum displacement (amplitude) A.
- The particle moves from x=A to x=√3A2 and then from x=√3A2 to x=A2.
- For the position x=A, the angle θ1 corresponding to this position is 0∘ (since it is at maximum displacement).
- For the position x=√3A2:
cos(θ1)=xA=√3A/2A=√32⟹θ1=30∘
- For the position x=A2:
cos(θ2)=xA=A/2A=12⟹θ2=60∘
- The angle covered when moving from x=A to x=√3A2 is:
Δθ1=θ1−0=30∘
- The angle covered when moving from x=√3A2 to x=A2 is:
Δθ2=θ2−θ1=60∘−30∘=30∘
- The total angle in one complete cycle (one period T) is 360∘.
- The time taken to cover 30∘ is:
t=30∘360∘×T=112T
- Thus, the time taken for both intervals is the same, 112T.
- The assertion states that the time taken to move from x=A to x=√3A2 is the same as the time taken to move from x=√3A2 to x=A2, which we found to be true.
- The reason states that the corresponding angles rotated in the reference circle are the same, which is also true.
Both the assertion and reason are correct.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Miscellaneous Examples
8 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Knowledge Check
The co-ordinates of a moving particles at time t, given by x=at2,y=bt2. The speed of the particle is
A2(a+b)tB(a2+b2)1/2 tC2(a2+b2)1/2tD(a+b)t
Find the time taken by the particle in going from x = (A)/2) to x=A Hint :Timetaken→goomx=0→x =A Time taken to go from x=0→x= (A)/(2)Requiredtime= t_(1) - t_(2)
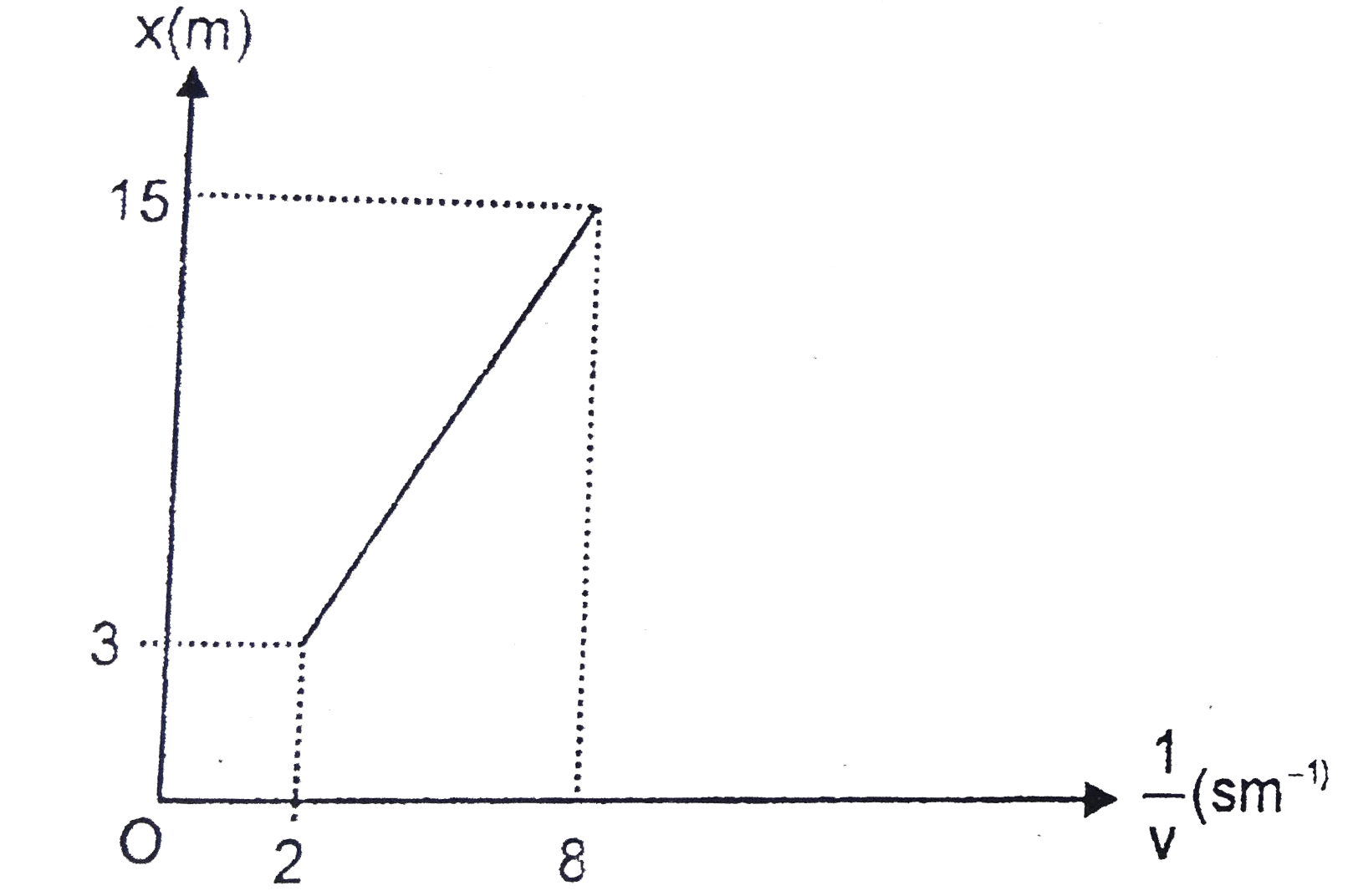
View SolutionGraph of position (x) vs inverse of velocity (1v) for a particle moving on a straight line is as shown. The time taken by the particle to move from x=3m to x=15 is :
View SolutionA particle executes SHM with a time period of 4s. Find the time taken by the particle to go directly from its mean position to half of its amplitude.
View SolutionA paricle performs S.H.M. with time period T. The time taken by the particle to move from hall the amplitude to the maximum dispalcement is T2
View SolutionA particle executing SHM with time period of 2s: Find the time taken by it to move from one amplitude to half the amplitude position.
View SolutionThe coordinates of a moving particle at any time t are given by x=ct and y=bt2. The speed of the particle is given by
View SolutionThe coordinate of a moving particle at any instant of time t are x = at and y=bt2. The trajectory of the particle is
View Solution
