A 0.5kg body performs simple harmonic motion with a frequency of 2Hz and an amplitude of 8mm. Find the maximum velocity of the body, its maximum acceleration and the maximum restoring force to which the body is subjected.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will find the maximum velocity, maximum acceleration, and maximum restoring force for a body performing simple harmonic motion (SHM) given its mass, frequency, and amplitude.
Given Data:
- Mass (m) = 0.5 kg
- Frequency (f) = 2 Hz
- Amplitude (A) = 8 mm = 8 × 10^-3 m
Step 1: Calculate Maximum Velocity (Vmax)
The formula for maximum velocity in SHM is given by:
Vmax=ωA
Where:
- ω (angular frequency) can be calculated using the formula:
ω=2πf
Calculating ω:
ω=2π(2)=4πrad/s
Now substituting ω and A into the maximum velocity formula:
Vmax=(4π)(8×10−3)
Calculating:
Vmax=32π×10−3
Vmax≈0.101m/s
Step 2: Calculate Maximum Acceleration (Amax)
The formula for maximum acceleration in SHM is given by:
Amax=ω2A
Substituting ω and A:
Amax=(4π)2(8×10−3)
Calculating:
Amax=16π2(8×10−3)
Amax≈1.264m/s2
Step 3: Calculate Maximum Restoring Force (Fmax)
The maximum restoring force can be calculated using Newton's second law:
Fmax=mAmax
Substituting the values:
Fmax=(0.5)(1.264)
Calculating:
Fmax≈0.632N
Final Answers:
- Maximum Velocity (Vmax) ≈ 0.101 m/s
- Maximum Acceleration (Amax) ≈ 1.264 m/s²
- Maximum Restoring Force (Fmax) ≈ 0.632 N
---
- Mass (m) = 0.5 kg
- Frequency (f) = 2 Hz
- Amplitude (A) = 8 mm = 8 × 10^-3 m
The formula for maximum velocity in SHM is given by:
Vmax=ωA
Where:
- ω (angular frequency) can be calculated using the formula:
ω=2πf
ω=2π(2)=4πrad/s
Vmax=(4π)(8×10−3)
Vmax=32π×10−3
Vmax≈0.101m/s
The formula for maximum acceleration in SHM is given by:
Amax=ω2A
Amax=(4π)2(8×10−3)
Amax=16π2(8×10−3)
Amax≈1.264m/s2
The maximum restoring force can be calculated using Newton's second law:
Fmax=mAmax
Fmax=(0.5)(1.264)
Fmax≈0.632N
- Maximum Velocity (Vmax) ≈ 0.101 m/s
- Maximum Acceleration (Amax) ≈ 1.264 m/s²
- Maximum Restoring Force (Fmax) ≈ 0.632 N
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Intro. Exer.
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.2
5 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Subjective
18 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
An object undergoes simple harmonic motion with a frequency of 1.6Hz and an amplitude of 4 mm. What is the acceleration at the maximum displacement from equilibrium ? What is the acceleration 0.4 seconds later?
View SolutionThe amplitude of a particle executing simple harmonic motion with a frequency of 60 Hz is 0.01 m. Determine the maximum value of the acceleration of the particle.
View Solution
Knowledge Check
A simple harmonic oscillator has a frequency of 2.5 Hz and an amplitude of 0.05m. What is the period of the oscillations?
A0.4sB0.2sC8sD20sA particle executing simple harmonic motion with an amplitude A and angularr frequency ω. The ratio of maximum acceleration to the maximum velocity of the particle is
AωABω2ACωDω2A
A body describes simple harmonic motion with an amplitude of 5 cm and a period of 0.2s. Find the acceleration and velocity of the body when the displacement is (a) 5cm, (b) 3cm, (c) 0 cm.
View SolutionA body is in simple harmonic motion with time period T = 0.5 s and amplitude A = 1 cm. Find the average velocity in the interval in which it moves from equilibrium position to half of its amplitude.
View SolutionTwo simple harmonic motions of angular frequency 100rads−1 and 1000rads−1 have the same displacement amplitude. The ratio of their maximum accelerations is
View SolutionA body is executing simple harmonic motion with an angular frequency 2 rad/s . The velocity of the body at 20 mm displacement, when the amplitude of motion is 60 mm is -
View SolutionA body is performing simple harmonic motion of amplitude A and time period T. The figure shown position-time graph of the body . At any time t, acceleration of the body is f, then which of the following graphs is/are appropriate?
View SolutionThe velocity-time graph of a body is given in. The maximum acceleration in ms−1 is .
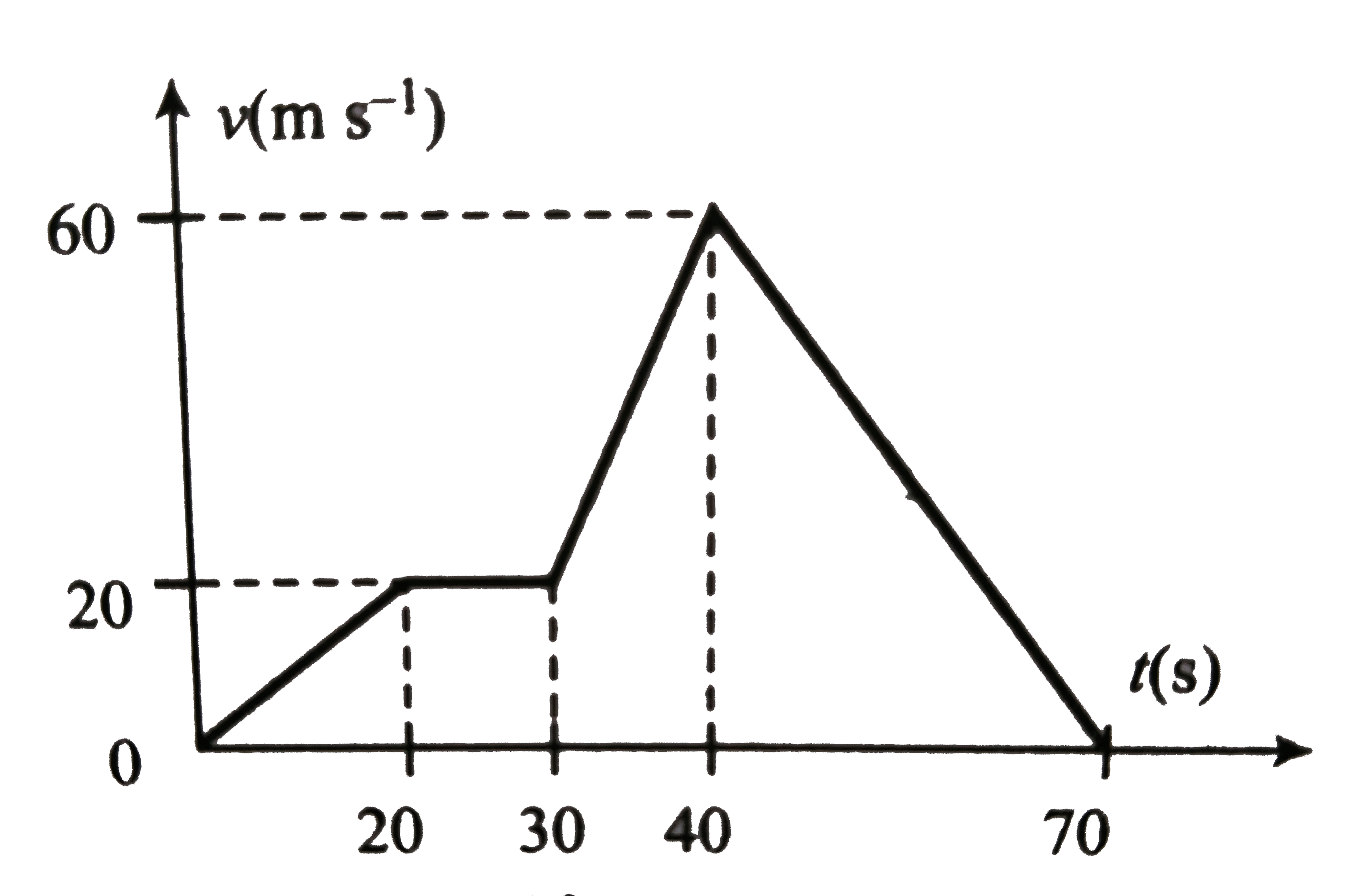 .
.
View Solution