Under isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
The correct Answer is:A, B, C, D
To find the surface tension of the soap in terms of the given parameters when two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r under isothermal conditions, we can follow these steps:
Step 1: Understand the excess pressure in soap bubbles
The excess pressure inside a soap bubble is given by the formula:
Pi=P0+4TR
where Pi is the internal pressure of the bubble, P0 is the external pressure, T is the surface tension, and R is the radius of the bubble.
Step 2: Write the equations for the two initial bubbles
For the two bubbles with radii r1 and r2, the internal pressures can be expressed as:
P1=P0+4Tr1
P2=P0+4Tr2
Step 3: Write the equation for the final bubble
After coalescing, the new bubble has a radius r and its internal pressure is:
P=P0+4Tr
Step 4: Apply the principle of conservation of volume
The total volume of the two smaller bubbles must equal the volume of the larger bubble:
43πr31+43πr32=43πr3
This simplifies to:
r31+r32=r3
Step 5: Set up the equation for pressures
Using the pressures from the bubbles, we can write:
P1V1+P2V2=PV
Substituting the volumes and pressures:
(P0+4Tr1)43πr31+(P0+4Tr2)43πr32=(P0+4Tr)43πr3
Step 6: Simplify the equation
Eliminating 43π from both sides:
(P0+4Tr1)r31+(P0+4Tr2)r32=(P0+4Tr)r3
Step 7: Expand and rearrange the equation
Expanding the left-hand side:
P0r31+4Tr1r31+P0r32+4Tr2r32=P0r3+4Trr3
Combining like terms gives:
P0(r31+r32)+4T(r31r1+r32r2)=P0r3+4Tr3r
Step 8: Solve for T
Rearranging to isolate T:
4T(r21+r22)=P0(r3−r31−r32)
Thus,
T=P0(r3−r31−r32)4(r21+r22)
Final Result
The surface tension T of the soap in terms of the given parameters is:
T=P0(r3−r31−r32)4(r21+r22)
The excess pressure inside a soap bubble is given by the formula:
Pi=P0+4TR
where Pi is the internal pressure of the bubble, P0 is the external pressure, T is the surface tension, and R is the radius of the bubble.
For the two bubbles with radii r1 and r2, the internal pressures can be expressed as:
P1=P0+4Tr1
P2=P0+4Tr2
After coalescing, the new bubble has a radius r and its internal pressure is:
P=P0+4Tr
The total volume of the two smaller bubbles must equal the volume of the larger bubble:
43πr31+43πr32=43πr3
This simplifies to:
r31+r32=r3
Using the pressures from the bubbles, we can write:
P1V1+P2V2=PV
Substituting the volumes and pressures:
(P0+4Tr1)43πr31+(P0+4Tr2)43πr32=(P0+4Tr)43πr3
Eliminating 43π from both sides:
(P0+4Tr1)r31+(P0+4Tr2)r32=(P0+4Tr)r3
Expanding the left-hand side:
P0r31+4Tr1r31+P0r32+4Tr2r32=P0r3+4Trr3
Combining like terms gives:
P0(r31+r32)+4T(r31r1+r32r2)=P0r3+4Tr3r
Rearranging to isolate T:
4T(r21+r22)=P0(r3−r31−r32)
Thus,
T=P0(r3−r31−r32)4(r21+r22)
The surface tension T of the soap in terms of the given parameters is:
T=P0(r3−r31−r32)4(r21+r22)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples21videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples10videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Two soap bubbles of radii a and b coalesce to form a single bubble of radius c. If the external pressure is P, find the surface tension of the soap solution.
View SolutionTwo soap bubbles of radii 2 cm and 4 cm join to form a double bubble in air, then radius of. curvature of interface is
View Solution
Knowledge Check
- Question 1 - Select One
Two spherical soap bubbles of radii r1andr2 in vaccum coalesce under isothermal conditions. The resulting bubble has a radius R such that
A(r1+r2)/2BR=[r1r2]/r1+r+(2)CR=√(r21+r22)DR=r1+r2 - Question 2 - Select One
The radii of two soap bubbles are r1andr2(r2<r1). They meet to produce a double bubble. The radius of their common interface is
Ar1r2r1+r2Br1+r22Cr1r2r1−r2Dr2−r1
Two soap bubble of different radii R1 and R2(<R1) coalesce to form an interface of radius R as shown in figure. The correct value of R is
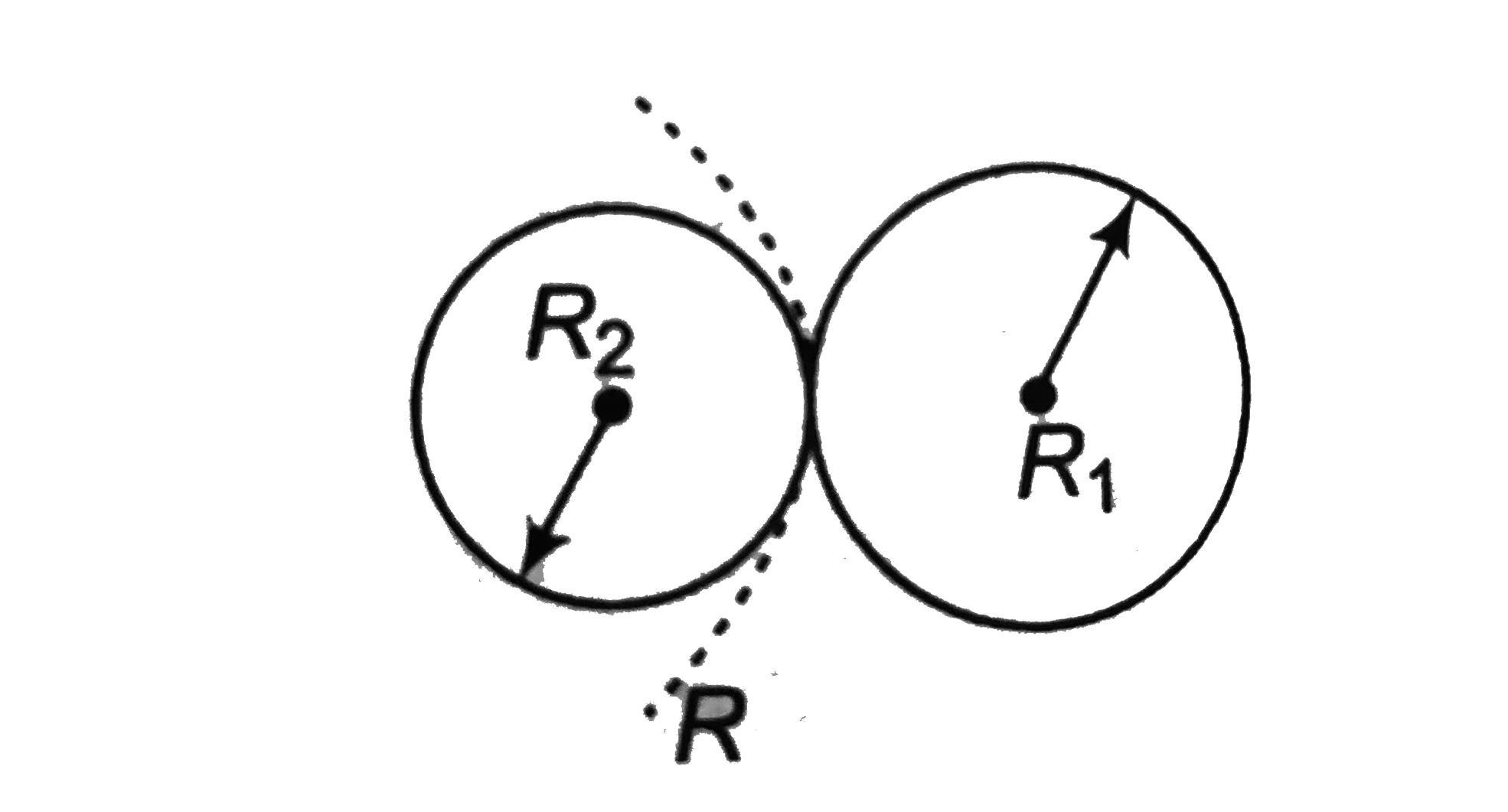 .View Solution
.View SolutionAir is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution is S, the work done in the process is
View SolutionA certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
View SolutionTwo identical soap bubbles each of radius r and of the same surface tension T combine to form a new soap bubble of radius R. The two bubbles contain air at the same temperature. If the atmospheric pressure is p0 then find the surface tension T of the soap solution in terms of p0, r and R. Assume process is isothermal.
View SolutionA soap bubble of radius 'r' is blown up to form a bubble of radius 2r under isothemal conditions. If σ be the surface tension of soap solution , the energy spent in doing so is
View SolutionTwo soap bubbles in vacuum of radius 3cm and4cm coalesce to form a single bubble, in same temperature. What will be the radius of the new bubble
View Solution

