A simple harmonic wave of amplitude 8 units travels along positive x-axis. At any given instant of time, for a particle at a distance of 10cm from the origin, the displacement is +6units, and for a particle at a distance of 25cm from the origin, the displacement is +4 units. Calculate the wavelength.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will use the standard equation of a simple harmonic wave and the given displacements at specific distances.
Step 1: Write down the wave equation
The standard equation for a simple harmonic wave traveling along the positive x-axis can be written as:
y(x,t)=Asin(2πλ(vt−x))
where:
- y is the displacement,
- A is the amplitude,
- λ is the wavelength,
- v is the wave speed,
- x is the position along the wave.
Step 2: Substitute the known values for the first particle
For the first particle at a distance x1=10cm, the displacement y1=6units:
6=8sin(2πλ(vt−10))
Dividing both sides by 8:
68=sin(2πλ(vt−10))
This simplifies to:
sin(2πλ(vt−10))=0.75
Taking the inverse sine:
2πλ(vt−10)=sin−1(0.75)
Calculating sin−1(0.75):
sin−1(0.75)≈0.848radians
Thus, we have:
2πλ(vt−10)=0.848(Equation 1)
Step 3: Substitute the known values for the second particle
For the second particle at a distance x2=25cm, the displacement y2=4units:
4=8sin(2πλ(vt−25))
Dividing both sides by 8:
48=sin(2πλ(vt−25))
This simplifies to:
sin(2πλ(vt−25))=0.5
Taking the inverse sine:
2πλ(vt−25)=sin−1(0.5)
Calculating sin−1(0.5):
sin−1(0.5)=π6radians
Thus, we have:
2πλ(vt−25)=π6(Equation 2)
Step 4: Set up the equations
From Equation 1:
2πλ(vt−10)=0.848
From Equation 2:
2πλ(vt−25)=π6
Step 5: Solve for vt in both equations
From Equation 1:
vt−10=0.848λ2π
From Equation 2:
vt−25=π6λ2π=λ12
Step 6: Set the two expressions for vt equal
Setting the two expressions for vt equal to each other:
0.848λ2π+10=λ12+25
Step 7: Solve for λ
Rearranging gives:
0.848λ2π−λ12=25−10
0.848λ2π−λ12=15
Finding a common denominator and solving for λ will yield:
λ=250cm
Final Answer:
The wavelength λ is 250cm.
---
The standard equation for a simple harmonic wave traveling along the positive x-axis can be written as:
y(x,t)=Asin(2πλ(vt−x))
where:
- y is the displacement,
- A is the amplitude,
- λ is the wavelength,
- v is the wave speed,
- x is the position along the wave.
For the first particle at a distance x1=10cm, the displacement y1=6units:
6=8sin(2πλ(vt−10))
Dividing both sides by 8:
68=sin(2πλ(vt−10))
This simplifies to:
sin(2πλ(vt−10))=0.75
Taking the inverse sine:
2πλ(vt−10)=sin−1(0.75)
Calculating sin−1(0.75):
sin−1(0.75)≈0.848radians
Thus, we have:
2πλ(vt−10)=0.848(Equation 1)
For the second particle at a distance x2=25cm, the displacement y2=4units:
4=8sin(2πλ(vt−25))
Dividing both sides by 8:
48=sin(2πλ(vt−25))
This simplifies to:
sin(2πλ(vt−25))=0.5
Taking the inverse sine:
2πλ(vt−25)=sin−1(0.5)
Calculating sin−1(0.5):
sin−1(0.5)=π6radians
Thus, we have:
2πλ(vt−25)=π6(Equation 2)
From Equation 1:
2πλ(vt−10)=0.848
From Equation 2:
2πλ(vt−25)=π6
From Equation 1:
vt−10=0.848λ2π
From Equation 2:
vt−25=π6λ2π=λ12
Setting the two expressions for vt equal to each other:
0.848λ2π+10=λ12+25
Rearranging gives:
0.848λ2π−λ12=25−10
0.848λ2π−λ12=15
Finding a common denominator and solving for λ will yield:
λ=250cm
The wavelength λ is 250cm.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.14videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Exercise 17.22videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Example Type 51videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
A particle executes simple harmonic motion with an amplitude of 4cm At the mean position the velocity of the particle is 10cm/s. distance of the particle from the mean position when its speed 5 cm/s is
View SolutionIf all the particles of a body is situated at distance d from origin, then the distance of CM of the body from origin is
View Solution
Knowledge Check
- Question 1 - Select One
Find the equation of the line , which is perpendicular to x - axis and a distance of 3 units from left of the origin is
Ax=3By=−3Cx=−3Dy=3
Velocity time graph for a particle moving in a line is given.
Calculate the displacement of the particle and distance travelled in first 4 seconds.
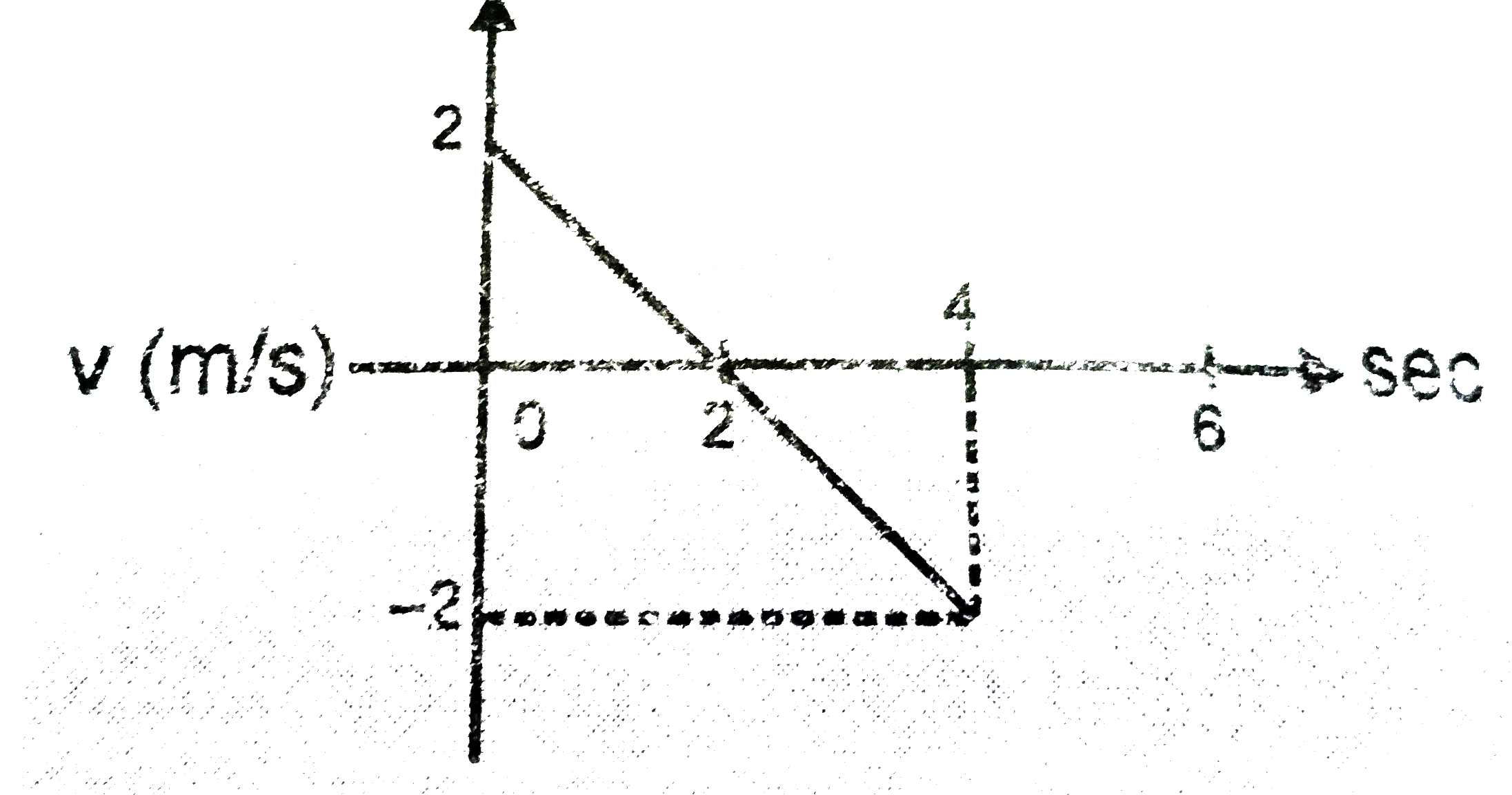 View Solution
View SolutionA transverse harmonic wave of amplitude 0.01 m is genrated at one end (x=0) of a long horizontal string by a tuning fork of frequency 500 Hz. At a given instant of time the displacement of the particle at x=0.1 m is -0.005 m and that of the particle at x=0.2 m is +0.005 m. calculate the wavelength and the wave velocity. obtain the equetion of the wave assuming that the wave is traveling along the + x-direction and that the end x=0 is at he equilibrium position at t=0.
View SolutionFind the equation of a line which is at a distance of 5 units from origin and the perpendicular from origin to this line makes an angle of 30∘ from the positive direction of X-axis.
View SolutionFor a particle executing SHM, x = displacement from mean position, v = velocity and a = acceleration at any instant, then
View SolutionFind the equation of a circle which touches y− axis at a distance of 4units from the origin and cuts an intercept of 6units along the positive direction of x−axis.
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
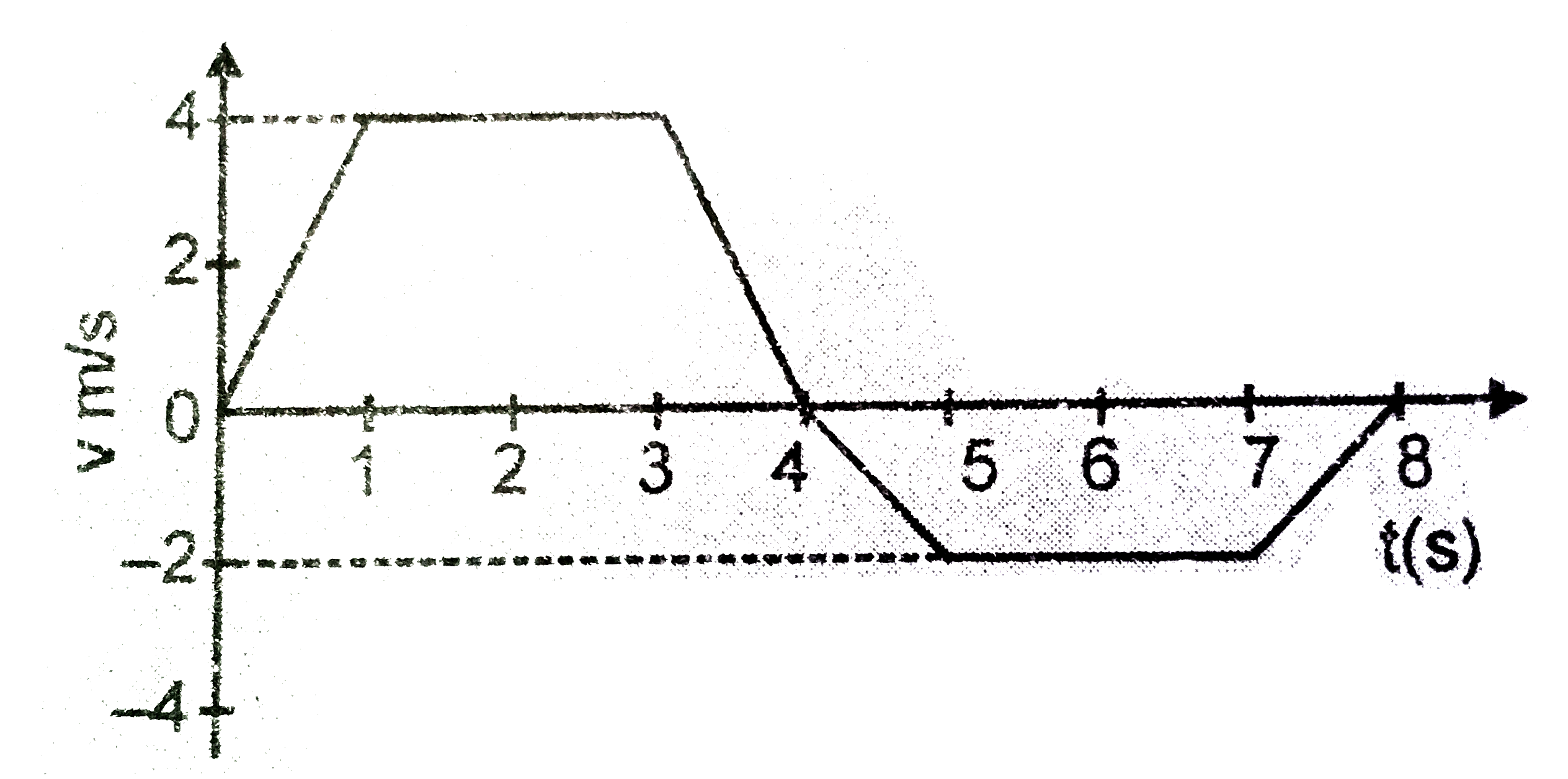 View Solution
View SolutionA particle executes shm with an amplitude of 10 cm and a period of 5 s. Find the velocity and acceleration of the particle of a distance 5 cm from the equilibrium position.
View Solution

