Two long strings A and B, each having linear mass density 1.2×10−2kgm−1, are stretched by different tensions 4.8 N and 7.5 N respectively and are kept parallel to each other with their left ends at x = 0. Wave pulses are produced on the strings at the left ends at t = 0 on string A and at t = 20 ms on string B. When and where will the pulse on B overtake that on A ?
The correct Answer is:A, B
To solve the problem of when and where the wave pulse on string B overtakes the wave pulse on string A, we will follow these steps:
Step 1: Determine the velocities of the wave pulses on both strings.
The velocity of a wave on a string is given by the formula:
v=√Tμ
where T is the tension in the string and μ is the linear mass density.
For String A:
- Tension T1=4.8N
- Linear mass density μ=1.2×10−2kg/m
Calculating the velocity v1:
v1=√4.81.2×10−2=√400=20m/s
For String B:
- Tension T2=7.5N
Calculating the velocity v2:
v2=√7.51.2×10−2=√625=25m/s
Step 2: Set up the equations for the distances traveled by both pulses.
Let t be the time taken for the pulses to meet after the pulse on string A is generated. The pulse on string B is generated 20 ms (0.02 s) later.
Distance traveled by pulse on String A:
xA=v1⋅t=20t
Distance traveled by pulse on String B:
Since the pulse on string B starts 0.02 s later, the time for string B is t−0.02:
xB=v2⋅(t−0.02)=25(t−0.02)
Step 3: Set the distances equal to find when they meet.
At the point of overtaking, the distances will be equal:
xA=xB
Substituting the expressions for xA and xB:
20t=25(t−0.02)
Step 4: Solve for t.
Expanding the equation:
20t=25t−0.5
Rearranging gives:
25t−20t=0.5
5t=0.5
t=0.55=0.1s
Step 5: Calculate the distance where they meet.
Substituting t=0.1 s into the equation for xA:
xA=20t=20×0.1=2m
Final Answer:
The pulse on string B overtakes the pulse on string A at t=0.1s and at a distance of 2m.
---
The velocity of a wave on a string is given by the formula:
- Tension T1=4.8N
- Linear mass density μ=1.2×10−2kg/m
- Tension T2=7.5N
Let t be the time taken for the pulses to meet after the pulse on string A is generated. The pulse on string B is generated 20 ms (0.02 s) later.
xA=v1⋅t=20t
Since the pulse on string B starts 0.02 s later, the time for string B is t−0.02:
xB=v2⋅(t−0.02)=25(t−0.02)
At the point of overtaking, the distances will be equal:
Expanding the equation:
5t=0.5
t=0.55=0.1s
Substituting t=0.1 s into the equation for xA:
The pulse on string B overtakes the pulse on string A at t=0.1s and at a distance of 2m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE MAINS50videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - ONLY ONE OPTION IS CORRECT62videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Level 2 Subjective7videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery9videos
VECTORS
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
Similar Questions
A standing wave is produced on a string on a string clamped at one end and free at the other. The length of the string
View Solutionn waves are produced on a string in 1s . When the radius of the string is doubled and the tension is maintained the same , the number of waves produced in 1s for the same harmonic will be
View SolutionA sting of length 1m and linear mass density 0.01 kg/m is stretched to a tension of 100 N. When both ends of the string are fixed, the three lowest frequencies for standing wave are f1,f2andf3 . When only one end of the string is fixed, the three lowest frequencies for standing wave are n1,n2andn3. Then,
View SolutionStationary waves are produced in 10 m long stretched string. If the string vibrates in 5 segments and wave velocity 20 m/s then the frequency is :-
View SolutionA taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
View SolutionA taut string having tension 100 N and linear mass density 0.25kg/m is used inside a cart to generate a wave pulse starting at the left end, as shown. What should be the velocity of the cart so that pulse remains stationary w.r.t. ground.
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N . A wave pulse is produced at t=0 near an ends as shown in Fig. 7.17 (b) , which travels towards the other end . When will the string have the shape shown in the Fig . ( c).
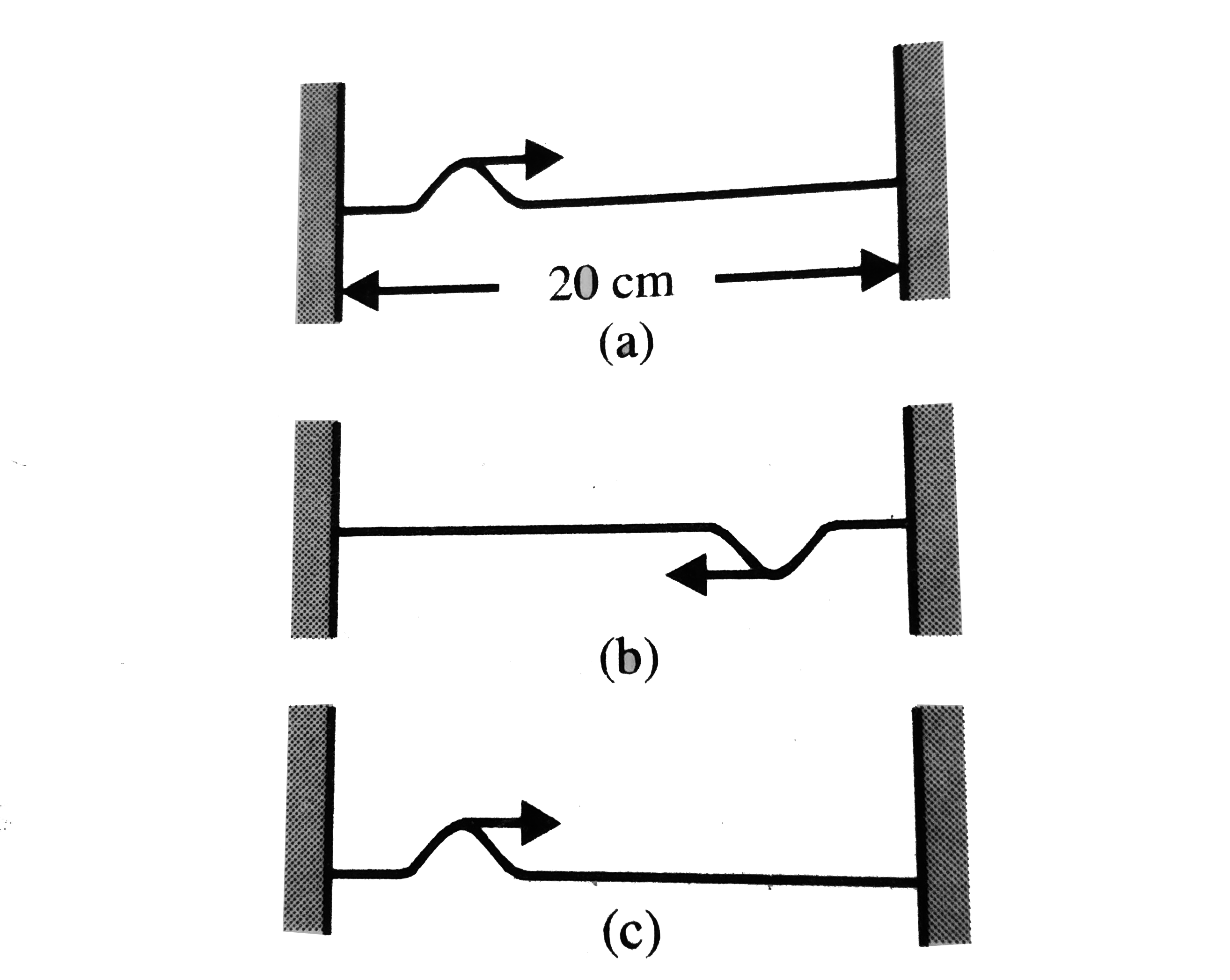 View Solution
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionTwo wave pulses identical in shape but inverted with respect to each other are produced at the two ends of a stretched string. At an instant when the pulses reach the middle, the string becomes completely straight. What happens to the energy of the two pulses ?
View Solution

