Find the resultant amplitude and phase of a point at which N sinusoidal waves interfere. All the waves have same amplitude A and their phases increase in arithmetic progression of common difference ϕ.
To find the resultant amplitude and phase of a point at which N sinusoidal waves interfere, we can follow these steps:
Step 1: Understand the Problem
We have N sinusoidal waves, each with the same amplitude A. The phases of these waves increase in an arithmetic progression with a common difference ϕ.
Step 2: Write the Expression for Each Wave
The n-th wave can be expressed as:
yn=Asin(kx−ωt+ϕn)
where ϕn=ϕ0+(n−1)ϕ for n=1,2,…,N.
Step 3: Calculate the Resultant Amplitude
To find the resultant amplitude R when these waves interfere, we can use the principle of superposition. The resultant amplitude can be derived from the vector addition of the individual wave amplitudes.
Using the sine addition formula, we can represent the resultant amplitude as:
R=A⋅sin(Nϕ2)sin(ϕ2)
Step 4: Derive the Phase of the Resultant Wave
The phase Φ of the resultant wave can be found by considering the average phase of the waves. The resultant phase can be expressed as:
Φ=ϕ0+(N−1)ϕ2
Step 5: Final Result
Thus, the resultant amplitude R and phase Φ of the point where N sinusoidal waves interfere are given by:
R=A⋅sin(Nϕ2)sin(ϕ2)
Φ=ϕ0+(N−1)ϕ2
We have N sinusoidal waves, each with the same amplitude A. The phases of these waves increase in an arithmetic progression with a common difference ϕ.
The n-th wave can be expressed as:
yn=Asin(kx−ωt+ϕn)
where ϕn=ϕ0+(n−1)ϕ for n=1,2,…,N.
To find the resultant amplitude R when these waves interfere, we can use the principle of superposition. The resultant amplitude can be derived from the vector addition of the individual wave amplitudes.
R=A⋅sin(Nϕ2)sin(ϕ2)
The phase Φ of the resultant wave can be found by considering the average phase of the waves. The resultant phase can be expressed as:
Φ=ϕ0+(N−1)ϕ2
Thus, the resultant amplitude R and phase Φ of the point where N sinusoidal waves interfere are given by:
R=A⋅sin(Nϕ2)sin(ϕ2)
Φ=ϕ0+(N−1)ϕ2
Similar Questions
Knowledge Check
Two sounds, waves, having sinusoidal wave from but different wavelengths and different amplitudes are said to have
Athe same quality but different intensityBdifferent quality but same intensityCsame quality and same intensityDdifferent quality and different intensity.Figure shows a sinusoidal wave at a given instant.
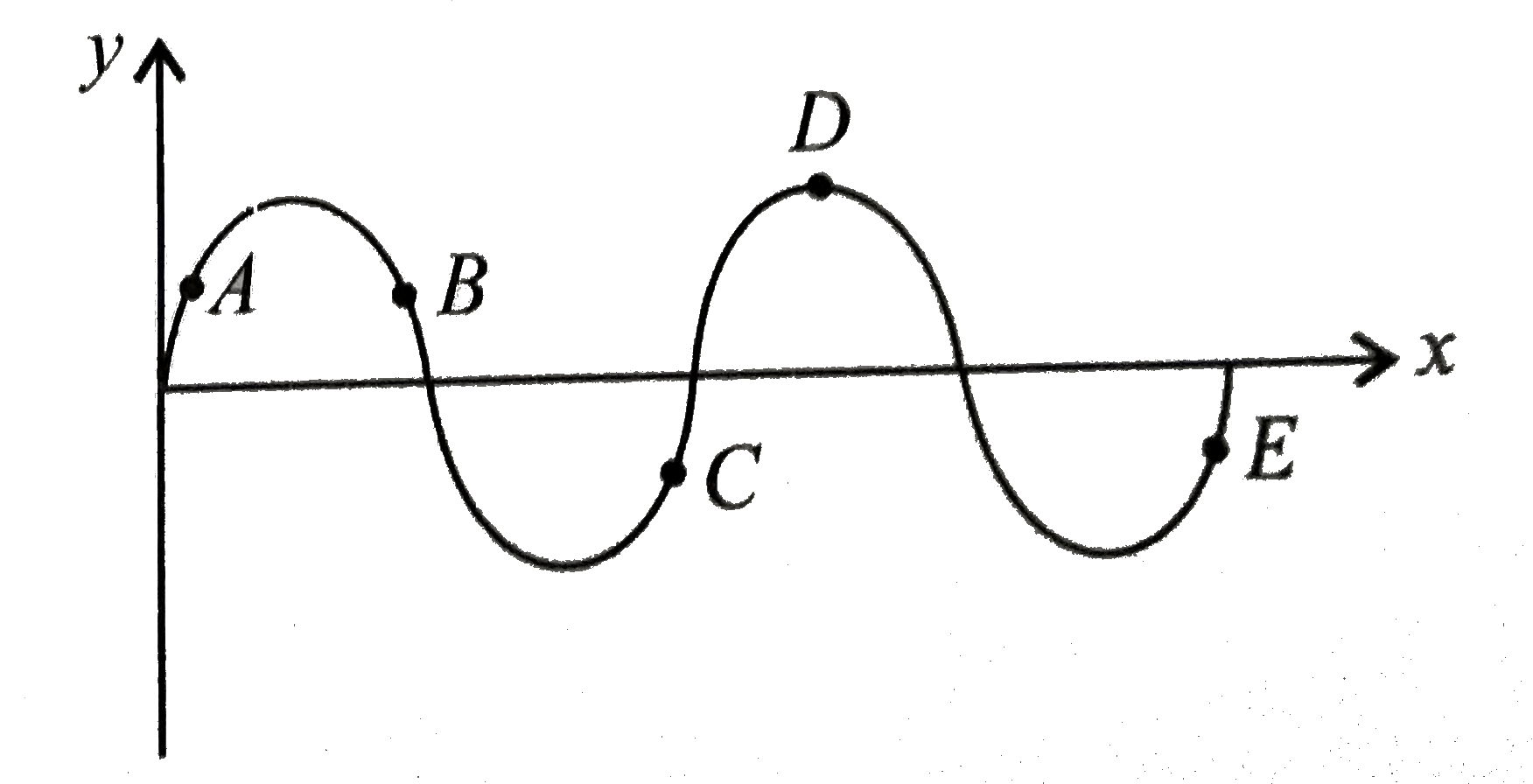
Which points are in phase?AA,BBB,CCB,DDC,E
The resultant amplitude, when two waves of two waves of same frequency but with amplitudes a1 and a2 superimpose at phase difference of π/2 will be :-
View SolutionDetermine the amplitudes of the resultant motion when two sinusoidal waves of same frequency , travelling in the same direction are combined . Their amplitudes are 3.0cmand4.0cm and they differ in phase by π/2radians.
View SolutionTwo bodies performing S.H.M. have same amplitude and frequency. Their phases at a certain instant are as shown in the figure. The phase difference between them is
_E01_002_Q01.png)
View SolutionThree coherent waves having amplitudes 12mm, 6mm and 4mm arrive at a given point with successive phase difference of π2. Then, the amplitude of the resultant wave is
View SolutionThree coherent waves having amplitudes 12mm, 6mm and 4mm arrive at a given point with successive phase difference of π2. Then, the amplitude of the resultant wave is
View SolutionFind the resultant amplitude and the phase difference between the resultant wave and the first wave , in the event the following waves interfere at a point , y1=(3cm)sinωt,
y2=(4cm)sin(ωt+π2),y3=(5cm)sin(ωt+π)
View Solution
