The harmonic wave yi=(2.0×10−3)cosπ(2.0x−50t) travels along a string towards a boundary at x=0 with a second string. The wave speed on the second string is 50m/s. Write expressions for reflected and transmitted waves. Assume SI units.
The correct Answer is:A, B, C
To solve the problem, we need to find the expressions for the reflected and transmitted waves based on the given incident wave and the properties of the two strings. Let's break it down step by step.
Step 1: Identify the Incident Wave
The incident wave is given by the equation:
yi=(2.0×10−3)cos(π(2.0x−50t))
Step 2: Determine the Wave Speed of the Incident Wave
The wave speed v1 of the incident wave can be calculated using the coefficients of t and x in the wave equation. The general form of a wave is:
y=Acos(kx−ωt)
where:
- ω is the angular frequency,
- k is the wave number.
From the given equation:
- Coefficient of t (angular frequency ω) = 50
- Coefficient of x (wave number k) = π×2
Using the formula for wave speed:
v1=ωk=502π
Calculating this gives:
v1=502=25m/s
Step 3: Determine the Wave Speed of the Second String
The wave speed of the second string is given as:
v2=50m/s
Step 4: Analyze the Mediums
Since v2>v1, we conclude that the second medium is a rarer medium. In a rarer medium, the reflected wave will have a positive phase shift.
Step 5: Calculate the Amplitude of the Reflected Wave
The amplitude of the reflected wave AR can be calculated using the formula:
AR=v2−v1v2+v1AI
where AI=2.0×10−3.
Substituting the values:
AR=50−2550+25×(2.0×10−3)
AR=2575×(2.0×10−3)=13×(2.0×10−3)=2.03×10−3m
Step 6: Calculate the Amplitude of the Transmitted Wave
The amplitude of the transmitted wave AT can be calculated using the formula:
AT=2v2v2+v1AI
Substituting the values:
AT=2×5050+25×(2.0×10−3)
AT=10075×(2.0×10−3)=43×(2.0×10−3)=8.03×10−3m
Step 7: Write the Expressions for the Reflected and Transmitted Waves
The general form of the reflected wave is:
yR=ARcos(kx−ωt)
Since the phase is positive for the reflected wave:
yR=2.03×10−3cos(π(2.0x−50t))
The transmitted wave will have a positive phase shift:
yT=ATcos(kx+ωt)
Thus:
yT=8.03×10−3cos(π(2.0x+50t))
Final Expressions
- Reflected Wave:
yR=2.03×10−3cos(π(2.0x−50t))
- Transmitted Wave:
yT=8.03×10−3cos(π(2.0x+50t))
The incident wave is given by the equation:
yi=(2.0×10−3)cos(π(2.0x−50t))
The wave speed v1 of the incident wave can be calculated using the coefficients of t and x in the wave equation. The general form of a wave is:
y=Acos(kx−ωt)
where:
- ω is the angular frequency,
- k is the wave number.
- Coefficient of t (angular frequency ω) = 50
- Coefficient of x (wave number k) = π×2
v1=ωk=502π
Calculating this gives:
v1=502=25m/s
The wave speed of the second string is given as:
v2=50m/s
Since v2>v1, we conclude that the second medium is a rarer medium. In a rarer medium, the reflected wave will have a positive phase shift.
The amplitude of the reflected wave AR can be calculated using the formula:
AR=v2−v1v2+v1AI
where AI=2.0×10−3.
AR=50−2550+25×(2.0×10−3)
AR=2575×(2.0×10−3)=13×(2.0×10−3)=2.03×10−3m
The amplitude of the transmitted wave AT can be calculated using the formula:
AT=2v2v2+v1AI
AT=2×5050+25×(2.0×10−3)
AT=10075×(2.0×10−3)=43×(2.0×10−3)=8.03×10−3m
The general form of the reflected wave is:
yR=ARcos(kx−ωt)
Since the phase is positive for the reflected wave:
yR=2.03×10−3cos(π(2.0x−50t))
yT=ATcos(kx+ωt)
Thus:
yT=8.03×10−3cos(π(2.0x+50t))
- Reflected Wave:
yR=2.03×10−3cos(π(2.0x−50t))
- Transmitted Wave:
yT=8.03×10−3cos(π(2.0x+50t))
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Assertion And Reason10videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Objective11videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Exercise 18.35videos
SUPERPOSITION OF WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
Similar Questions
A wave yi=0.3cos(2.0x−40t) is travelling along a string toward a boundary at x=0. Write expressions for the reflected waves if .
(a) the string has a fixed end at x=0 and
(b) The string has a free end at x=0.
Assume SI units.View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string . The juction of the strings is at x=0. The equation of the reflected wave is
View SolutionA harmonic wave is travelling on string 1. At a junction with string 2 it is partly reflected and partly transmitted. The linear mass density of the second string is four times that of the first string, and that the boundary between the two strings is at x=0. If the expression for the incident wave is
yi=Aicos(k1x−ω1t)
(a) What are the expressions for the transmitted and the reflected waves in terms of Ai,k1 and ω1?
(b) Show that the average power carried by the incident wave is equal to the sum of the average power carried by the transmitted and reflected waves.View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A . The junction of the strings is at x=0. The equation fo the refelcted wave is :
View SolutionA wave pulse on a string on a string has the dimension shown in figure. The wave speed is v=1 cm /s . If point O is a free end. The shape of wave at time t = 3s si
 View Solution
View SolutionThe displacement wave in a string is y=(3cm)sin6.28(0.5x−50t) where x is in centimetres and t in seconds. The velocity and wavelength of the wave is :-
View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string. The reflected wave has amplitude 0.5A. The junction of the string is at x=0 The equation of the reflected is :
View SolutionThe wave described by y =0.25sin(10πx−2πt) where x and y are in meters and t in seconds , is a wave travelling along the
View SolutionTransverse waves travel with a speed of 20.0m/sin a string under a tension of 6.00 N. what tension is requared for a wave speed of 30.0m/s in the same string?
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
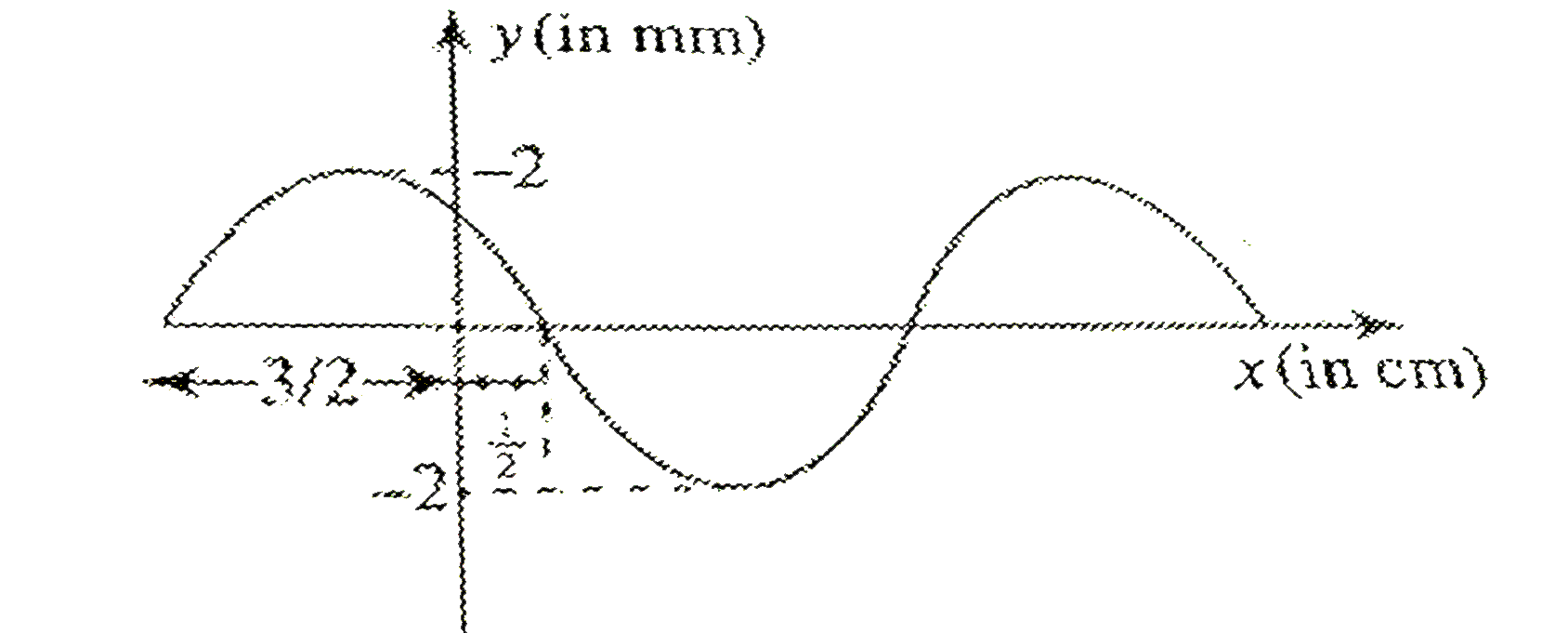
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.View Solution

