A thin taut string tied at both ends and oscillating in its third harmonic has its shape described by the equation y(x,t)=(5.60cm)sin[(0.0340radcm)x]sin[(50.0rads)t], where the origin is at the left end of the string, the x-axis is along the string and the y-axis is perpendicular to the string.
(a) Draw a sketch that shows the standing wave pattern.
(b)Find the amplitude of the two travelling waves that make up this standing wave.
(c) What is the length of the string?
(d) Find the wavelength, frequency, period and speed of the travelling wave.
(e) Find the maximum transverse speed of a point on the string.
(f) What would be the equation y(x,t) for this string if it were vibrating in its eighth harmonic?
The correct Answer is:A, B, C, D
(a)
Third harmonic
(b) A=5.62=2.8cm
(c) k=0.034cm−1
λ=2πk=184.7cm
l=3λ2=277cm
(d) λ=184.7cm
f=ω2π=502π=7.96Hz.
T=1f=0.126s
v=fλ=1470cm/s
(e) vmax=ωAmax
= (50)(5.60)
=280cm/s
(f) Frequency and hence ω will become 8/3 times.
∴ω'=50×83=133rad/s
k=ωv or k∝ω
Hence, k will become 83 times.
k'=(83)(0.034)=0.0907rad/cm.
Topper's Solved these Questions
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Single Correct
15 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 More Than One Correct
6 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 1 Subjective
24 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
Similar Questions
the equation for the vibration of a string fixed both ends vibration in its third harmonic is given by
y = 2 cm sin [(0.6cm−1x)×]cos[(500ps−1t]What is the position of node?
View SolutionA stretched string is fixed at both its ends. Three possible wavelengths of stationary wave patterns that can be set up in the string are 90 cm, 60 cm and 45 cm. the length of the string may be
View Solution
Knowledge Check
One end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
Ay(t)=Asin(2πx)6cos(50πt)3By(t)=Asin(πx)3cos(100πt)3Cy(t)=Asin(5πx)6cos(255πt)3Dy(t)=Asin(5πx)2cos250πt
A string is clamped at both the ends and it is vibrating in its 4th harmonic. The equation of the stationary wave is Y=0.3sin(0.157x)cos(200πt). The length of the string is : (All quantities are in SI units.)
View SolutionThe equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by y=(0.4cm)sin[(0.314cm−1)x]cos[f(600πs−1)t].(a) What is the frequency of vibration ? (b) What are the positions of the nodes ? (c) What is the length of the string ? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration ?
View SolutionThe equation of a standing wave, produced on a string fixed at both ends, is y=(0.4cm)sin[(0.314cm−1)x]cos[(600πs−1)t] What could be the smallest length of the string ?
View SolutionA transversee wave propagating on the string can be described by the equationy=2sin(10x+300t) , where x and y are in metres and t in second. If the vibrating string has linear density of 0.6×10−3g/cm , then the tension in the string is
View SolutionA standing wave pattern of maximum amplitude 2 mm is obtained in a string whose shape at t = 0 is represented in the graph.
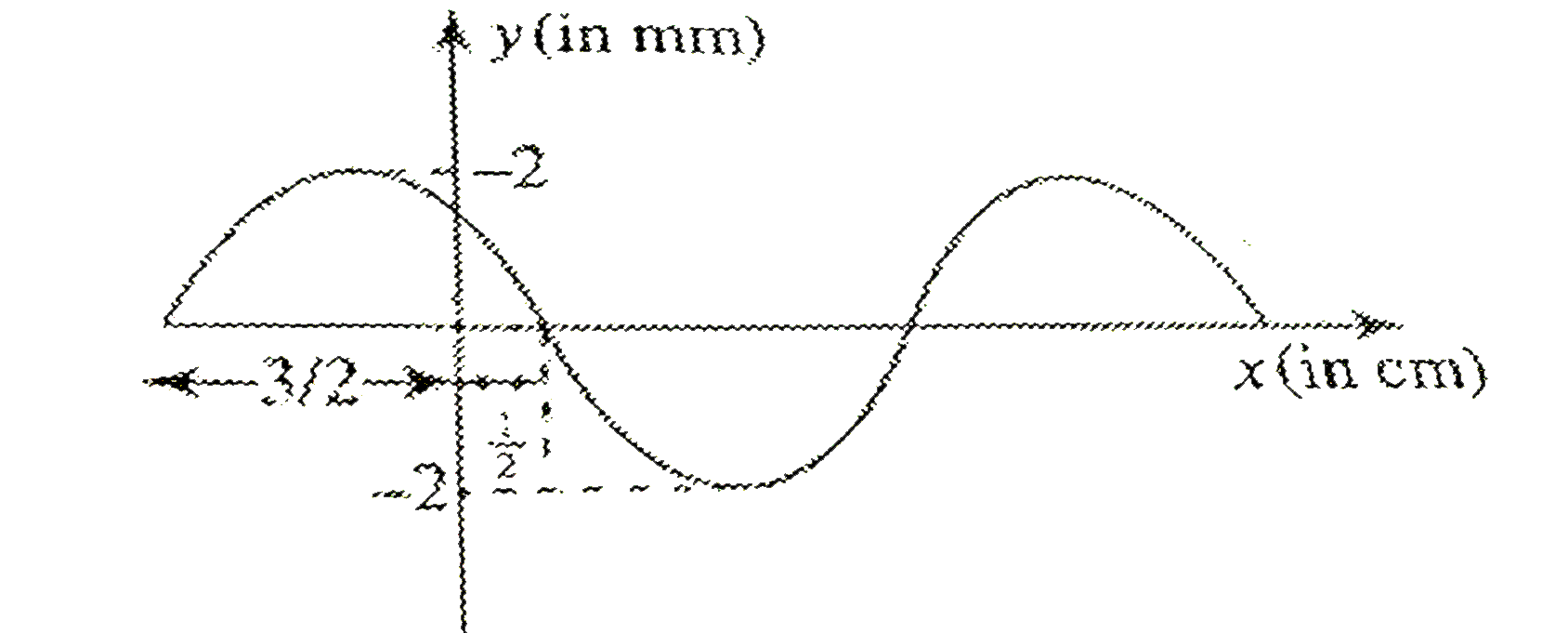
If the speed of the travelling wave in the string is 5 cm/s, then find the component waves.
View SolutionA travelling wave y=Asin(kx−ωt+θ) passes from a heavier string to a lighter string . The juction of the strings is at x=0. The equation of the reflected wave is
View SolutionThe linear density of a vibrating string is 10−4kg/m. A transverse wave is propagating on the string, which is described by the equation y=0.02sin(x+30t), where x and y are in metres and time t in seconds. Then tension in the string is
View Solution
