Write the equation for the fundamental standing sound waves in a tube that is open at both ends. If the tube is 80cm long speed of wave is 330m/s . Represent the amplitude of the wave at an antinode by A .
The correct Answer is:A, B, C
To find the equation for the fundamental standing sound waves in a tube that is open at both ends, we will follow these steps:
Step 1: Understand the conditions for a tube open at both ends
In a tube that is open at both ends, the fundamental frequency (first harmonic) has antinodes at both ends. The length of the tube corresponds to half the wavelength of the sound wave.
Step 2: Calculate the wavelength
The relationship between the length of the tube (L) and the wavelength (λ) for the fundamental mode is given by:
L=λ2
From this, we can express the wavelength as:
λ=2L
Given that the length of the tube L=80cm=0.8m, we can calculate:
λ=2×0.8m=1.6m
Step 3: Calculate the fundamental frequency
The fundamental frequency (f) can be calculated using the formula:
f=vλ
where v is the speed of sound. Given v=330m/s:
f=330m/s1.6m≈206.25Hz
Step 4: Write the equation for the standing wave
The general equation for a standing wave can be expressed as:
S(x,t)=Asin(kx)cos(ωt)
where:
- A is the amplitude of the wave,
- k is the wave number, given by k=2πλ,
- ω is the angular frequency, given by ω=2πf.
Calculating k:
k=2π1.6≈3.93m−1
Calculating ω:
ω=2π×206.25≈1292.5s−1
Final Equation
Substituting A, k, and ω into the standing wave equation, we get:
S(x,t)=Asin(3.93x)cos(1292.5t)
Summary
The equation for the fundamental standing sound wave in a tube that is open at both ends, with a length of 80 cm and a wave speed of 330 m/s, is:
S(x,t)=Asin(3.93x)cos(1292.5t)
In a tube that is open at both ends, the fundamental frequency (first harmonic) has antinodes at both ends. The length of the tube corresponds to half the wavelength of the sound wave.
The relationship between the length of the tube (L) and the wavelength (λ) for the fundamental mode is given by:
L=λ2
From this, we can express the wavelength as:
λ=2L
Given that the length of the tube L=80cm=0.8m, we can calculate:
λ=2×0.8m=1.6m
The fundamental frequency (f) can be calculated using the formula:
f=vλ
where v is the speed of sound. Given v=330m/s:
f=330m/s1.6m≈206.25Hz
The general equation for a standing wave can be expressed as:
S(x,t)=Asin(kx)cos(ωt)
where:
- A is the amplitude of the wave,
- k is the wave number, given by k=2πλ,
- ω is the angular frequency, given by ω=2πf.
k=2π1.6≈3.93m−1
ω=2π×206.25≈1292.5s−1
Substituting A, k, and ω into the standing wave equation, we get:
S(x,t)=Asin(3.93x)cos(1292.5t)
The equation for the fundamental standing sound wave in a tube that is open at both ends, with a length of 80 cm and a wave speed of 330 m/s, is:
S(x,t)=Asin(3.93x)cos(1292.5t)
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Subjective Questions
1 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 2 Single Correct
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Level 1 Objective
34 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
If a man at the equator would weight (3/5)th of his weight, the angular speed of the earth is:
View SolutionWhat is maximum possible wavelength of standing waves in 1m long string if it is fixed at both ends
View SolutionThe distance between consecutive crest and trough of a wave is 10cm. If the speed of wave is 200cms. Then the time period of wave is
View SolutionThe vibrations from an 800 Hz tuning fork set up standing waves in a string clamped at both ends. The wave speed in the string is known to be 400m/s for the tension used. The standing wave is observed to have four antinodes. How long is the string?
View SolutionTwo sound waves one in air and the other in fresh water are equal in intensity.
(a) Find the ratio of pressure amplitude of the wave in water to that of the wave in air.
(b) If the pressure amplitudes of the waves are equal then what will be the ratio of the intensities of the waves.
[Vsound=340m/s in air & density of air =1.25kg/m3,Vsound=1530m/s in water, density of water =1000kg/m3]
View SolutionWrite the relation for the speed of electromagnetic wave in terms of the amplitudes of electric and magnetic fields.
View SolutionA tube of a certain diameter and of length 48cm is open at both ends. Its fundamental frequency is found to be 320Hz. The velocity of sound in air is 320m/sec. Estimate the diameter of the tube.
View SolutionA tube of a certain diameter and of length 48cm is open at both ends. Its fundamental frequency is found to be 320Hz. The velocity of sound in air is 320m/sec. Estimate the diameter of the tube.
One end of the tube is now closed. Calculate the lowest frequency of resonance for the tube.
View SolutionFor the wave shown in figure, write the equation of this wave if its position is shown at t=0. Speed of wave is v=300m/s.
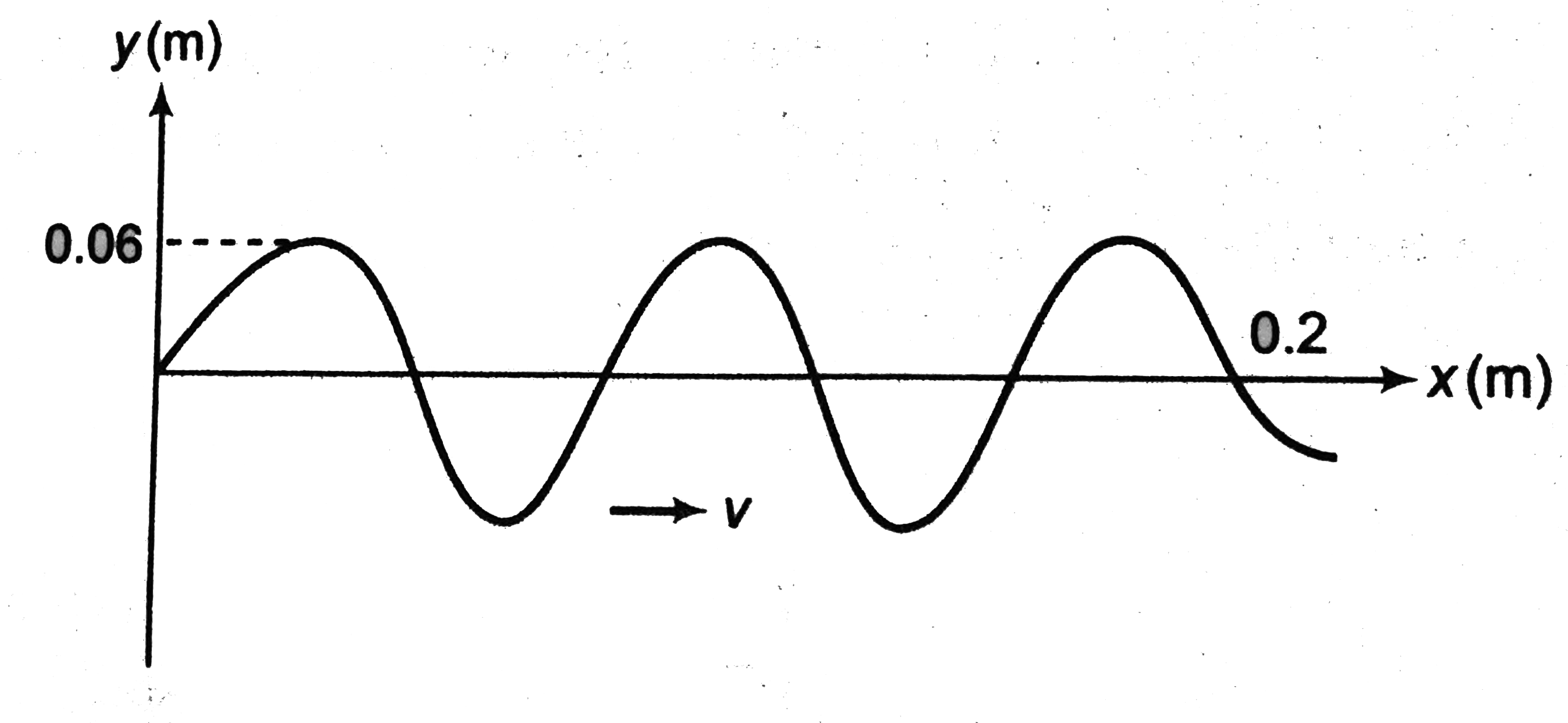
View SolutionSix antinodes are observed in the air column when a standing wave forms in a Kundt's tube . What is the length of the air column if steel bar of 1m length is clamped at the middle .
The velocity of sound in steel is 5250m/s and in air 343m/s.
View Solution
