Two loudspeakers radiate in phase at 170HZ. An observer sits at 8m from one speaker and 11m from the other . The intensity level from either speaker acting alone is 60dB. The speed of sound is 340m/s. Find the observer intensity when both speakers are on together.
The correct Answer is:A, B, C, D
To find the observer's intensity when both speakers are on together, we can follow these steps:
Step 1: Calculate the wavelength (λ)
The speed of sound (v) is given as 340 m/s, and the frequency (f) is given as 170 Hz. The wavelength can be calculated using the formula:
λ=vf
Substituting the values:
λ=340m/s170Hz=2m
Step 2: Calculate the path difference (Δx)
The observer is 8 m from one speaker and 11 m from the other. The path difference (Δx) is:
Δx=|d2−d1|=|11m−8m|=3m
Step 3: Calculate the phase difference (Δφ)
The phase difference (Δφ) can be calculated using the formula:
Δϕ=2πΔxλ
Substituting the values:
Δϕ=2π⋅3m2m=3π
Step 4: Calculate the intensity from each speaker (I1 and I2)
The intensity level (L) from either speaker acting alone is given as 60 dB. We can convert this to intensity (I) using the formula:
L=10log10(II0)
Where I0=10−12W/m2 (the reference intensity). Rearranging gives:
I=I0⋅10L10=10−12⋅106010=10−12⋅106=10−6W/m2
Step 5: Calculate the total intensity when both speakers are on
When both speakers are on, the total intensity (I) can be calculated using the formula:
I=I1+I2+2√I1I2cos(Δϕ)
Since I1=I2=I:
I=I+I+2Icos(3π)=2I+2I(−1)=2I−2I=0
Conclusion
The observer's intensity when both speakers are on together is:
I=0W/m2
The speed of sound (v) is given as 340 m/s, and the frequency (f) is given as 170 Hz. The wavelength can be calculated using the formula:
The observer is 8 m from one speaker and 11 m from the other. The path difference (Δx) is:
The phase difference (Δφ) can be calculated using the formula:
The intensity level (L) from either speaker acting alone is given as 60 dB. We can convert this to intensity (I) using the formula:
When both speakers are on, the total intensity (I) can be calculated using the formula:
The observer's intensity when both speakers are on together is:
Topper's Solved these Questions
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.1
4 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.2
4 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Comprehension Based Questions
2 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SUPERPOSITION OF WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SUPERPOSITION OF WAVESEXERCISE - Level 2 Subjective
8 Videos
Similar Questions
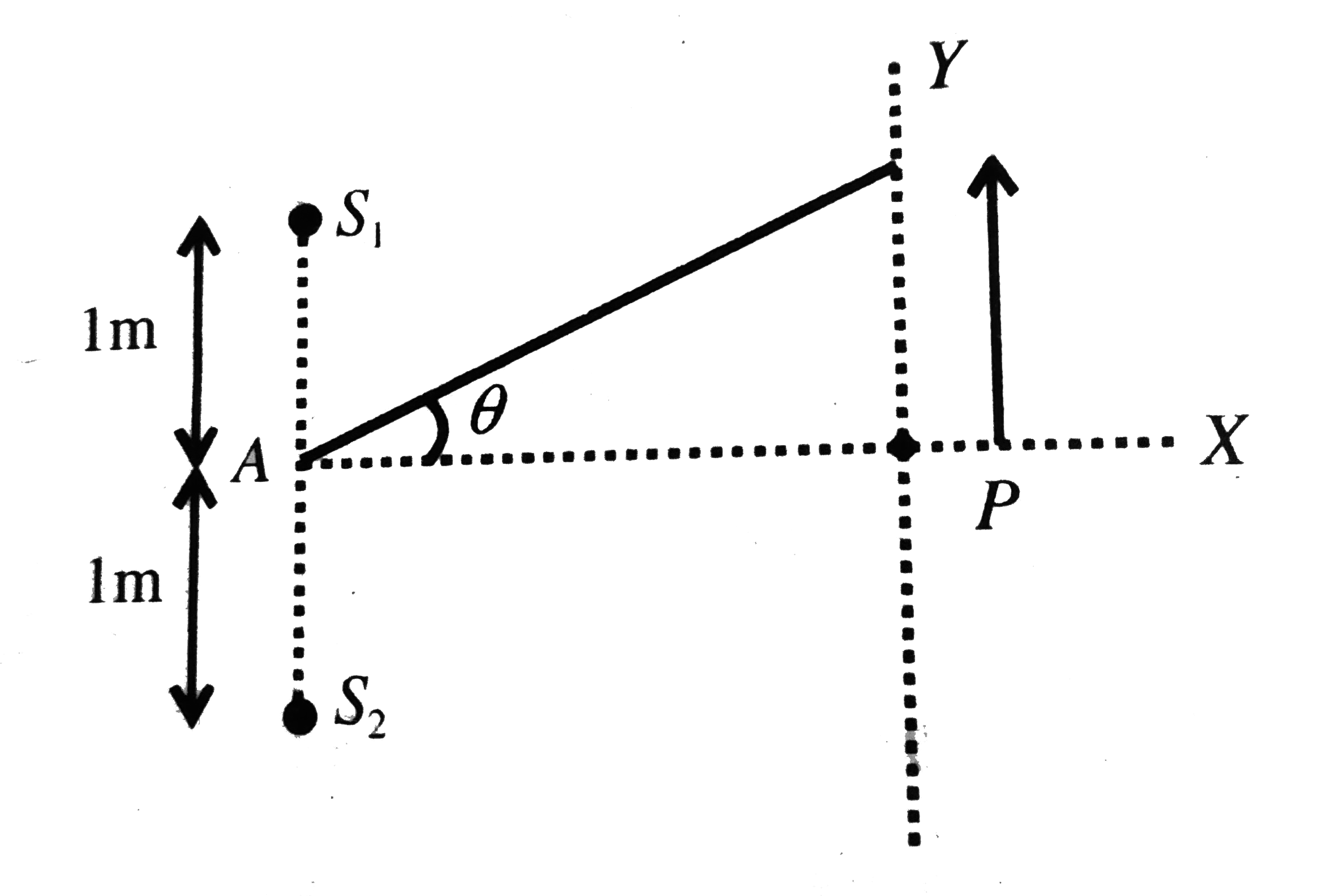
Two speakers S1andS2 derived by the same amplifier and placed at y=1.0mandy=−1.0m (Fig . 7.9) The speakers vibrate in phase at 600Hz. A man stands at a point on the x - axis at a very large distance from the origin and starts moving parallel to the Y - axis . The speed of sound in air is 330m/s.
(a). At what angle will the intensity of sound drop to a minimum for the first time ?
(b) At what angle will the sound intensity be maximum for the first time ?
(c ) If he continues to walk along the line , how many more maxima can he hear ?
View SolutionTwo identical speakers emit sound waves of frequency 680HZ uniformly in all directions with a total audio output of 1mW each. The speed of sound in air is 340m/s. A point P is a distance 2.00m from one speaker and 3.00m from the other.
(a) Finf the intensity I1 and I2 from rach speaker at point p separately.
(b) If the speakers are driven coherently and in phase, what is the intensity at point p?
(c ) If they driven coherently but of phase by 180∘, what is the intensity at point P?
(d) If the speakers are incoherent, what is the intensity at point p?
View Solutiontwo pipes have each of length 2 m, one is closed at on end and the other is open at both ends. The speed of sound in air is 340 m/s . The frequency at which both can resonate is ?
View SolutionTwo speakers separeted by some distance emit sound of the same frequency. At some point P the intensity due to each speaker separately is Io. The path difference from P to one of the speakers is 12λ greater than that from P to the other speaker. What is the intensity at P if
(a) the speakers are coherent and in phase,
(b) the speakers are incoherent, and
(c ) the speakers are coherent but have a phase different of 180∘?
View SolutionAn observer A fires a gun and another observer B at a distance 1650 m away from A hears its sound. If the speed of sound is 330 m/s, Find the time when B will hear the sound after firing by A.
View SolutionTwo electric trains run at the same speed of 72kmh−1 along the same track and in the same direction with a separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340ms−1, find the frequencies heard by the person.
View SolutionThe time interval between a lightning flash and the first sound of thunder is 5 s. If the speed of sound in air is 330 m s−1, find the distance of flash from the observer.
View SolutionFigure shows a tube having sound source at one end and observe at other end. Source produces frequencies upto 10000Hz. Speed of sound is 400m/s. Find the frequencies at which person hears maximum intensity.

View SolutionAn observer A fires a gun and another observer B at a distance 1650 m away from A hears its sound. If the speed of sound is 330 m s−1, find the time when B will hear the sound after firing by A.
View SolutionThe smoke from the gun barrel is seen 2 second before the explosion is heard. If the speed of sound in air is 340 ms−1, calculate the distance of observer from gun. State the approximation used.
View Solution