A piece of metal floats on mercury. The coefficient of volume expansion of metal and mercury are γ1andγ2, respectively. if the temperature of both mercury and metal are increased by an amount ΔT, by what factor does the frection of the volume of the metal submerged in mercury changes ?
The correct Answer is:A, B, D
To solve the problem, we need to analyze how the fraction of the volume of the metal submerged in mercury changes when both the metal and mercury are heated by a temperature change ΔT.
1. Understand the Initial Condition:
- Let the density of the metal be ρs and the density of mercury be ρl.
- The fraction of the volume of the metal submerged in mercury can be expressed as:
f0=ρsρl
2. Apply the Volume Expansion Formula:
- When the temperature increases by ΔT, the new densities of the metal and mercury can be expressed using their coefficients of volume expansion γ1 and γ2:
ρ′s=ρs1+γ1ΔT
ρ′l=ρl1+γ2ΔT
3. Calculate the New Fraction:
- The new fraction of the volume of the metal submerged in mercury after the temperature increase becomes:
f=ρ′sρ′l=ρs1+γ1ΔTρl1+γ2ΔT=ρsρl⋅1+γ2ΔT1+γ1ΔT
- Substituting f0 into the equation gives:
f=f0⋅1+γ2ΔT1+γ1ΔT
4. Simplify the Expression:
- For small values of γ1ΔT and γ2ΔT (which is often the case in thermal expansion problems), we can use the approximation:
1+x1+y≈1+(x−y)for small x and y
- Applying this approximation:
f≈f0⋅(1+(γ2−γ1)ΔT)
5. Final Result:
- Thus, the fraction of the volume of the metal submerged in mercury changes by a factor of:
f≈f0⋅(1+(γ2−γ1)ΔT)
- Let the density of the metal be ρs and the density of mercury be ρl.
- The fraction of the volume of the metal submerged in mercury can be expressed as:
f0=ρsρl
- When the temperature increases by ΔT, the new densities of the metal and mercury can be expressed using their coefficients of volume expansion γ1 and γ2:
ρ′s=ρs1+γ1ΔT
ρ′l=ρl1+γ2ΔT
- The new fraction of the volume of the metal submerged in mercury after the temperature increase becomes:
f=ρ′sρ′l=ρs1+γ1ΔTρl1+γ2ΔT=ρsρl⋅1+γ2ΔT1+γ1ΔT
- Substituting f0 into the equation gives:
f=f0⋅1+γ2ΔT1+γ1ΔT
- For small values of γ1ΔT and γ2ΔT (which is often the case in thermal expansion problems), we can use the approximation:
1+x1+y≈1+(x−y)for small x and y
- Applying this approximation:
f≈f0⋅(1+(γ2−γ1)ΔT)
- Thus, the fraction of the volume of the metal submerged in mercury changes by a factor of:
f≈f0⋅(1+(γ2−γ1)ΔT)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Exercise 20.37videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Exercise 20.43videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Exercise 20.15videos
THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary30videos
THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASES
- BOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason2videos
UNIT AND DIMENSIONS
Similar Questions
State true/false:
S1 : Hydrostatic pressure is a scalar quantity even though pressure is force divided by area and force is a vector quantity?
S2: A barometer made of a very narrow tube (see figure) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018/.∘C and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C but the temperature of the atmosphere does not change. Then, the mercury height in the tube remains unchanged.
S3 A block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
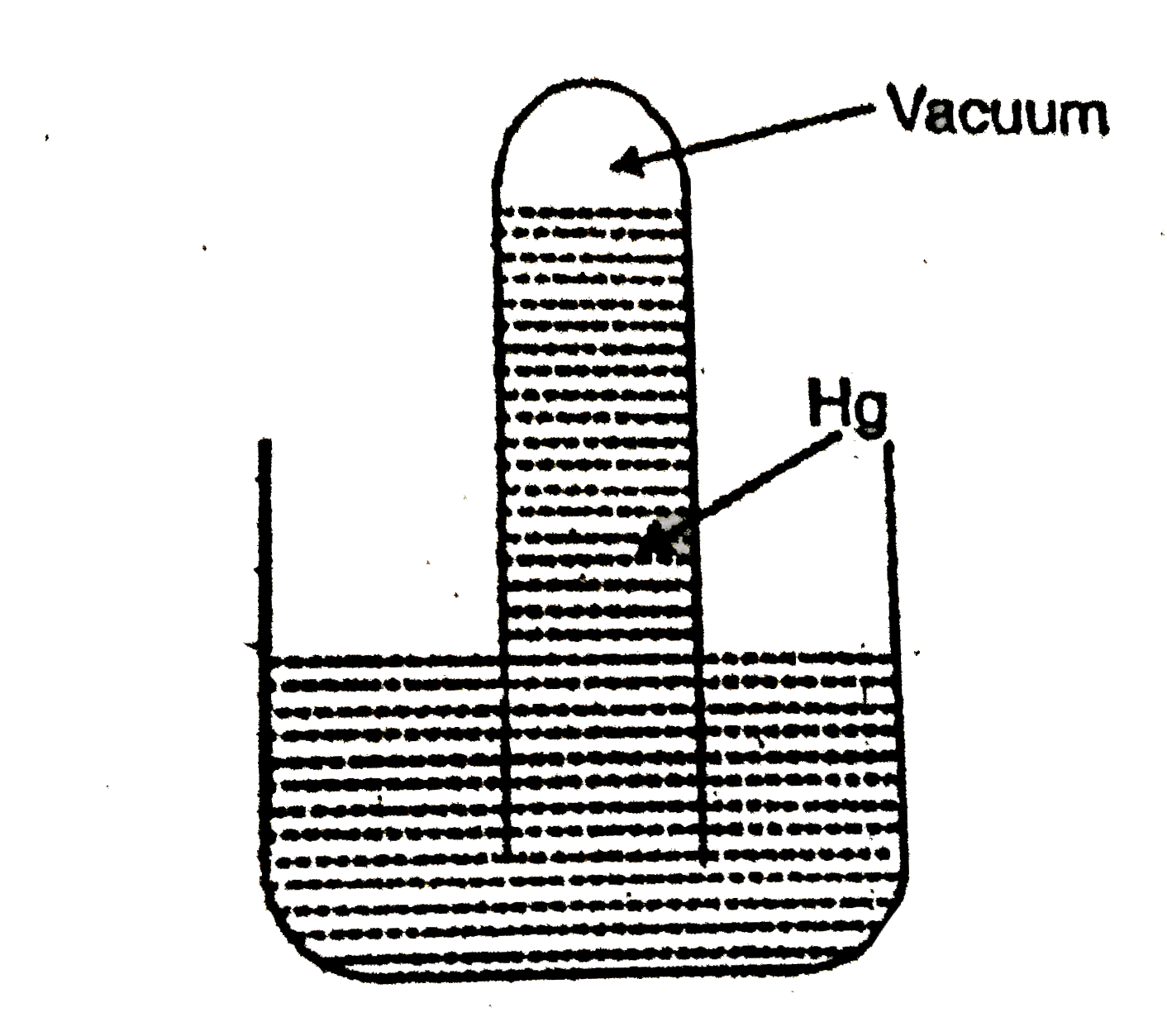 View Solution
View SolutionThe radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ΔT so that its new temperature is T+ΔT. The increase in the volume of the sphere is approximately
View Solution
Knowledge Check
- Question 1 - Select One
The radius of metal sphere at room temperature T is R and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature T, so that new temperature is T+ΔT. The increase in volume of sphere is approximately
A2πRαΔTBπR2αΔTC4πR3αΔT/3D4πR3αΔT - Question 2 - Select One
The volume of a block of a metal changes by 0.12% when it is heated through 20∘C . The coefficient of linear expansion of the metal is
A4×10−5∘C−1B2×10−5∘C−1C0.5×10−5∘C−1D4×10−4∘C−1
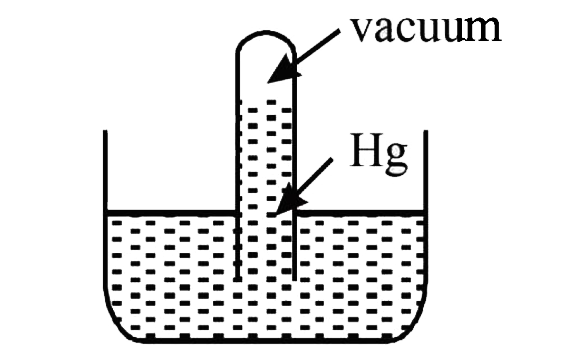
A barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
 View Solution
View SolutionA solid is immersed completely in a liquid. The temperature coefficients of volume expansion of solid and the liquid are γ1 and γ2(<γ1). If temperatures of both are increased, then match the following.
∣∣ ∣ ∣ ∣ ∣ ∣∣Table-1Table-2(A)upthrust on the solid will(P)increase(B)apparent weight of the solid will(Q)decrease(C)fraction of volume immersed in(R)remain samethe liquid if allowed to float will∣∣ ∣ ∣ ∣ ∣ ∣∣View SolutionA glass cylinder contains m0=100g of mercury at a temperature of t0=0∘C. When temperature becomes t1=20∘C the cylinder contains m1=99.7g of mercury The coefficient of volume expansion of mercury γHe=18×(10−5/∘C Assume that the temperature of the mercury is equal to that of the cylinder. The coefficient of linear expansion of glass α is
View SolutionA glass cylinder contains m0=100g of mercury at a temperature of t0=0∘C. When temperature becomes t1=20∘C the cylinder contains m1=99.7g of mercury The coefficient of volume expansion of mercury γHe=18×(10−5/∘C Assume that the temperature of the mercury is equal to that of the cylinder. The corfficient of linear expansion of glass α is
View SolutionA constant volume gas thermometer shows pressure readings of 60 cm and 90 cm of mercury at 0∘C and 100∘C respectively. What is the temperature on gas scale, when pressure reading is 70 cm of mercury?
View SolutionThe apparent coefficients of volume expansion of a liquid when heated filled in vessel A and B of identical volumes, are found to be γ1 and γ2 respectively. If α1 be the coefficient of liner expansion for A, then what will be the be the coefficient of linear expansion for B? (True expansion - vessel expansion = app.exp)
View Solution

