How many degress of freedom have the gas molecules, if under standard conditions the gas density is ρ=1.3kg/m3 and velocity of sound propagation o it is v=330m/s ?
To find the degrees of freedom of gas molecules given the gas density and the velocity of sound, we can follow these steps:
Step 1: Write down the equation for the velocity of sound in a gas.
The velocity of sound v in a gas is given by the formula:
v=√γPρ
where:
- γ is the adiabatic index (ratio of specific heats),
- P is the pressure of the gas,
- ρ is the density of the gas.
Step 2: Rearrange the equation to solve for γ.
From the equation above, we can rearrange it to find γ:
γ=ρv2P
Step 3: Substitute the known values into the equation.
Given:
- ρ=1.3kg/m3
- v=330m/s
- Standard atmospheric pressure P=1.013×105Pa
Substituting these values into the equation for γ:
γ=1.3×(330)21.013×105
Step 4: Calculate γ.
Calculating the numerator:
1.3×(330)2=1.3×108900=141570
Now, calculate γ:
γ=1415701.013×105≈1.4
Step 5: Relate γ to the degrees of freedom f.
The relationship between γ and the degrees of freedom f is given by:
γ=1+2f
Rearranging this gives:
2f=γ−1
Substituting γ=1.4:
2f=1.4−1=0.4
Step 6: Solve for f.
Now, we can solve for f:
f=20.4=5
Conclusion
The degrees of freedom of the gas molecules is f=5.
---
The velocity of sound v in a gas is given by the formula:
v=√γPρ
where:
- γ is the adiabatic index (ratio of specific heats),
- P is the pressure of the gas,
- ρ is the density of the gas.
From the equation above, we can rearrange it to find γ:
γ=ρv2P
Given:
- ρ=1.3kg/m3
- v=330m/s
- Standard atmospheric pressure P=1.013×105Pa
γ=1.3×(330)21.013×105
Calculating the numerator:
1.3×(330)2=1.3×108900=141570
Now, calculate γ:
γ=1415701.013×105≈1.4
The relationship between γ and the degrees of freedom f is given by:
γ=1+2f
Rearranging this gives:
2f=γ−1
Substituting γ=1.4:
2f=1.4−1=0.4
Now, we can solve for f:
f=20.4=5
The degrees of freedom of the gas molecules is f=5.
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Single Correct
12 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct
7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 1 Objective
10 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
Due to point isotropic sound source, the intensity at a point is observed as 40 dB. The density of air is ρ=(1511)kgm3 and velocity of sound in air is 330ms. Based on this information answer the following questions.
Q. The ratio of displacement amplitude of wave at observation point to wavelength of sound waves is
View SolutionDue to point isotropic sound source, theintensity at a point is observed as 40 dB. The density of air is ρ=(1511)kgm3 and velocity of sound in air is 330ms. Based on this information answer the following questions.
Q. The pressure amplitude at the observation point is
View SolutionIf the density of air at NTP is 1.293kg/m3 and γ=1.41, then the velocity of sound in air at NTP is :
View SolutionDue to a point isotropic sonic source, loudness at a point is L=60dB If density of air is ρ=(1511)kgm3 and velocity of sound in air is v=33ms, the pressure oscillation amplitude at the point of observation is [I0=10−12Wm2]
View SolutionThe maximum variation in pressure P that the ear can tolerate in Ioud sound is about 28N/m2. What is the corresponding maximum displacement for a sound of frequency 500Hz imart? Density of air is 1.22kg/m3 and velocity of sound =330m/s.
View SolutionAn open organ pipe of length 11cm in its fundamental mode vibrates in resonance with the first overtone of a closed organ pipe of length 13.2cm filled with some gas . If the velocity of sound in air is 330m/s, calculate the velocity of sound in the unknown gas .
View SolutionA thin metal plate is being bombarded by a perpendicular beal of gas particles from both sides as shown in the figure. The solid dots are representing the melecules hitting from left side and the faint dots are the molecules hitting frm right side. The mass of these gas particles is m=10−26kg and velocity before hitting is v0=5m/s. Volume density of the gas particles on both sides is n=1025 per m3. Each beam has an area A=1m2 and the collisions are perfectly elatic. What is the external force F (in newton) required to move the plate with a constant velocity v=2m/s

View SolutionThe density of a polyatomic gas in stantard conditions is 0.795kgm−3. The specific heat of the gas at constant
View SolutionA stationary sound sound 's' of frequency 334 Hz and a stationary ovserver 'O' are placed near a reflecting suface moving away from the source with velocity 2 m/s as shown in the figure. If the velocity of the sound waves is air is v= 330 m/s the apparent frequency of the echo is
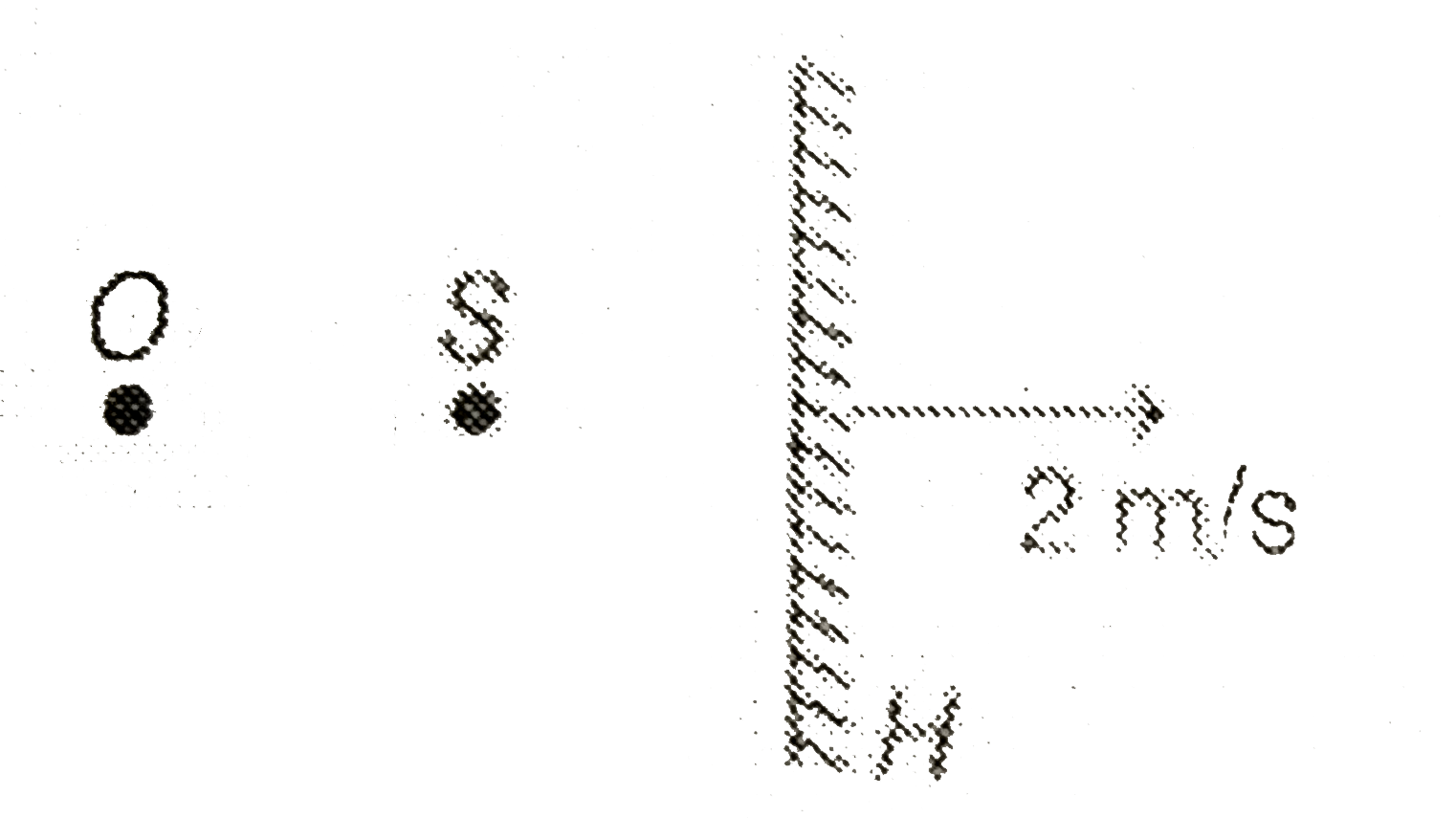
View SolutionCalculate height (Approx) of atmosphere considering density of atmosphere is uniform (ρ=1.3kg/m3)
View Solution
