One gram mole NO2at47∘C and 2 atm pressure in kept in a vessel. Assuming the molecules to be moving with (rms) velocity. Find the number of collisions per which the molecules make with one square metre area of the vessel wall.
The correct Answer is:A, B, C
To solve the problem of finding the number of collisions per second that 1 gram mole of NO2 at 47°C and 2 atm pressure makes with one square meter area of the vessel wall, we will follow these steps:
Step 1: Convert Temperature to Kelvin
We need to convert the given temperature from Celsius to Kelvin.
T(K)=T(°C)+273=47+273=320K
Step 2: Calculate the RMS Velocity
The formula for the root mean square (RMS) velocity (vrms) of gas molecules is given by:
vrms=√3RTM
Where:
- R=8.314J/(mol K) (universal gas constant)
- T=320K
- M=46×10−3kg/mol (molar mass of NO2)
Substituting the values:
vrms=√3×8.314×32046×10−3
Calculating this gives:
vrms≈423m/s
Step 3: Calculate the Mass of One Molecule
The mass of one molecule of NO2 can be calculated using:
m=MNA
Where NA=6.022×1023molecules/mol (Avogadro's number).
Substituting the values:
m=46×10−36.022×1023≈7.64×10−26kg
Step 4: Use the Pressure Equation
The pressure P of the gas can be expressed as:
P=FA=ΔpΔt⋅A
Where Δp is the change in momentum and Δt is the time interval. The change in momentum for a molecule colliding with the wall is:
Δp=2mvrms
Thus, the pressure can be rewritten as:
P=2mvrmsnA
Where n is the number of molecules colliding with the wall per second per square meter.
Step 5: Rearrange to Find n
Rearranging the equation to solve for n:
n=P⋅A2mvrms
Substituting P=2atm=2×1.013×105Pa and A=1m2:
n=(2×1.013×105)⋅12⋅(7.64×10−26)⋅(423)
Calculating this gives:
n≈3.1×1027collisions/m2/s
Final Answer
The number of collisions per second that the molecules make with one square meter area of the vessel wall is approximately:
3.1×1027
We need to convert the given temperature from Celsius to Kelvin.
T(K)=T(°C)+273=47+273=320K
The formula for the root mean square (RMS) velocity (vrms) of gas molecules is given by:
vrms=√3RTM
Where:
- R=8.314J/(mol K) (universal gas constant)
- T=320K
- M=46×10−3kg/mol (molar mass of NO2)
vrms=√3×8.314×32046×10−3
Calculating this gives:
vrms≈423m/s
The mass of one molecule of NO2 can be calculated using:
m=MNA
Where NA=6.022×1023molecules/mol (Avogadro's number).
Substituting the values:
m=46×10−36.022×1023≈7.64×10−26kg
The pressure P of the gas can be expressed as:
P=FA=ΔpΔt⋅A
Where Δp is the change in momentum and Δt is the time interval. The change in momentum for a molecule colliding with the wall is:
Δp=2mvrms
Thus, the pressure can be rewritten as:
P=2mvrmsnA
Where n is the number of molecules colliding with the wall per second per square meter.
Rearranging the equation to solve for n:
n=P⋅A2mvrms
Substituting P=2atm=2×1.013×105Pa and A=1m2:
n=(2×1.013×105)⋅12⋅(7.64×10−26)⋅(423)
Calculating this gives:
n≈3.1×1027collisions/m2/s
The number of collisions per second that the molecules make with one square meter area of the vessel wall is approximately:
3.1×1027
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Single Correct
12 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct
7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 1 Objective
10 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
1g mole of oxygen at 27∘C and (1) atmosphere pressure is enclosed in a vessel.
(a) Assuming the molecules to be moving with (vrms, find the number of collisions per second which the molecules make with one square metre area of the vessel wall.
(b) The vessel is next thermally insulated and moves with a constant speed (v0. It is then suddenly stoppes. The process results in a rise of temperature of the temperature of the gas by 1∘C. Calculate the speed v0.[k=1.38×10−23J/K and NA=6.02×1023/mol].
View SolutionOne mole of SO2 at 298K and 1atm pressure is heated in a closed vessel so that its temperature is 475K and pressure is 4atm. It is then cooled so that temperature becomes 298K and pressure is 1atm. What is that change in the internal energy of the gas?
View Solution
Knowledge Check
N molecules each of mass m of gas A and 2 N molecules each of mass 2m of gas B are contained in the same vessel which is maintined at a temperature T. The mean square of the velocity of the molecules of B type is denoted by v2 and the mean square of the x-component of the velocity of a tye is denoted by ω2. What is the ratio of ω2/v2=?
A3:2B1:3C2:3D1:1A2 litre vessel is filled with air at 50∘C and pressure of 3 atm. The temperature is now raised to 200∘C A valve is now opened so that the pressure inside drops to one atm What fraction of the total number of moles, inside escaped on openig the valve ? Assume no change in the volume of the container .
A7.7B9.9C8.9D0.77
One mole of oxygen occupies a volume of 24 L at 20∘C and 1 atm pressure. What is the rms speed of an oxygen? Find the total translational kinetic energy and the total momentum of the molecules.
View SolutionHydrogen gas is contained in a closed vessel at 1atm(100kPa) and 300K.(a) Calculate the mean speed of the molecules. (b) Suppose the molecules strike the wall with this speed making an average angle of 45∘with it. How many molecules strike each squre metre of the wall per second?
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
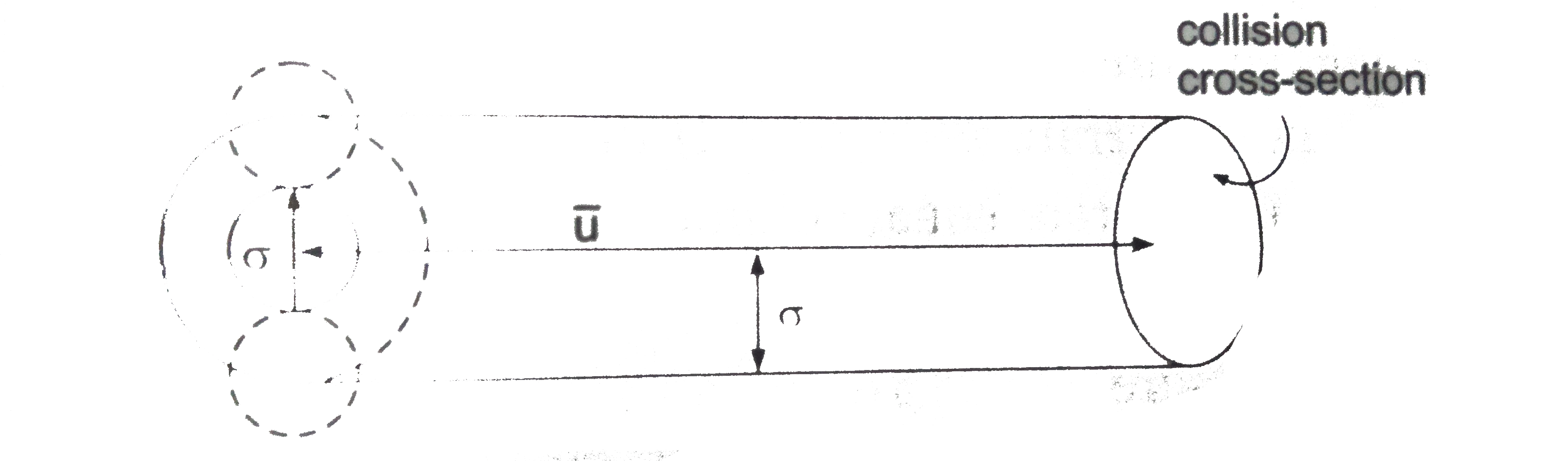
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
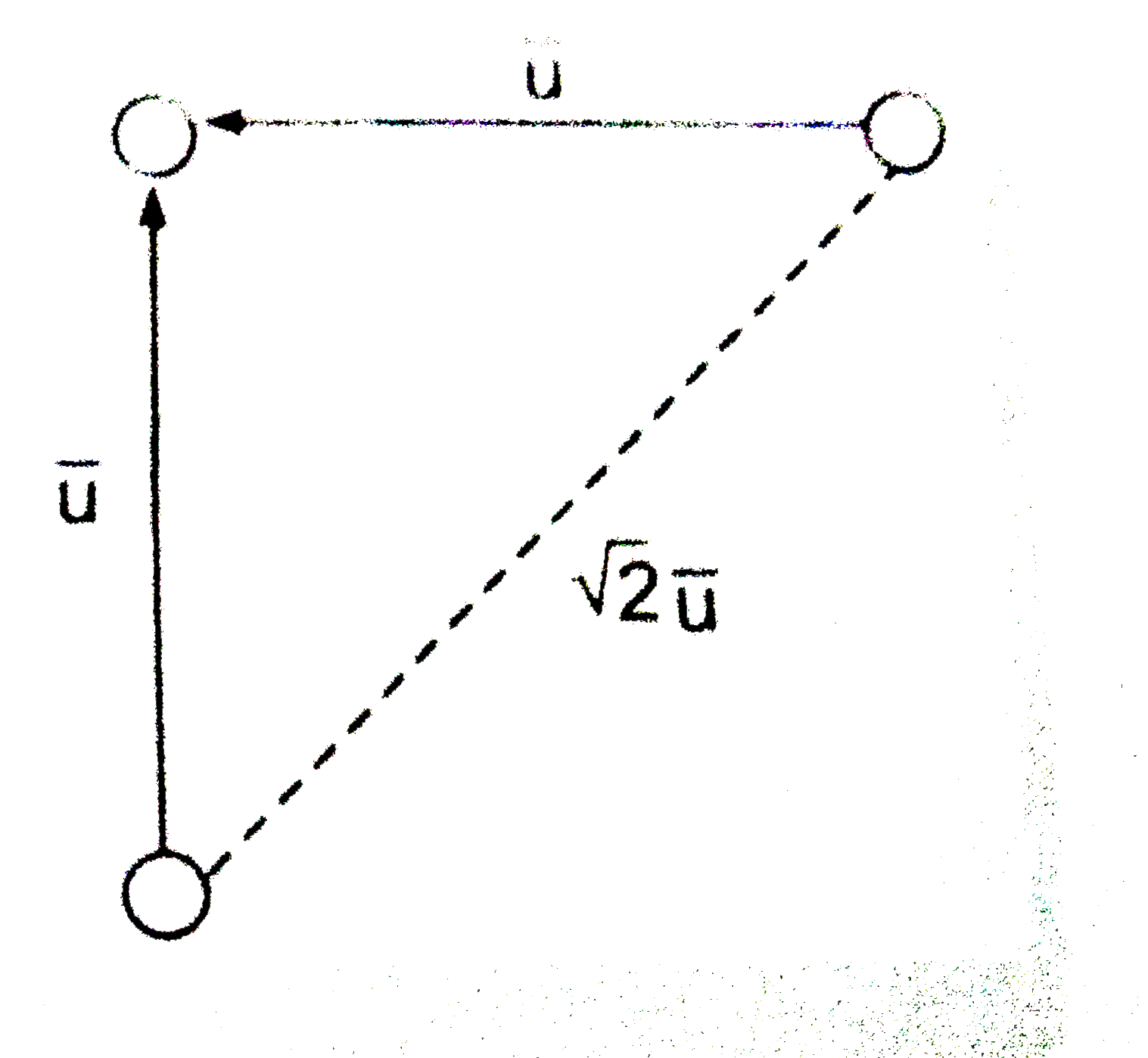
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionAt 127∘C and 1.00×10−2 atm pressure, the density of a gas is 1.24×10−2kgm−3.
a. Find vrms for the gas molecules.
b. Find the molecular weight of the gas and identify it.
View SolutionA small ball is projected at an angle α with an initial velocity u between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic and distance between the walls be d2, find.
(a) maximum height atained by the ball.
(b) total number of collisions with the walls before the ball comes back to the ground, and
(c) point at which the ball finally falls. The walls are supposed to be very tall.

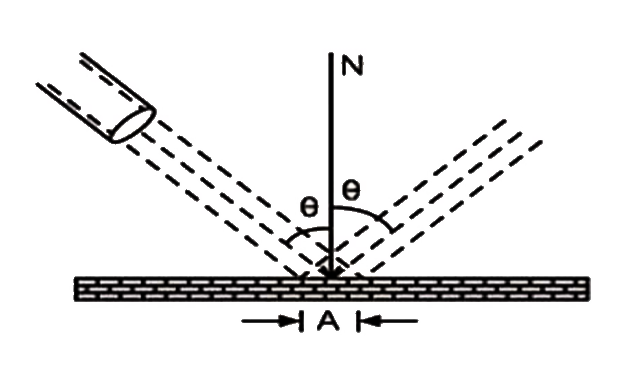
View SolutionA nozzle throws a stream of gas against a wall with a velocity v much larger than the thermal agitation of the molecules. After collision of the molecules with wall the magnitude of their velocity remains same. Also assume that the force exerted on the wall by the molecule is perpendicular to wall. (This is not strictly true for a rough wall.) Find the pressure exerted on the wall. (n = number of molecules per unit volume, m = mass of a gas molecule)
View Solution
