In a very good vacuum system in the laboratory, the vacuum attained was 10−13atm. If the temperature of the system was 300K, the number of molecules present in a volume of 1cm3 is.
2.4×106
24
2.4×109
zero
The correct Answer is:A
To find the number of molecules present in a volume of 1 cm³ at a pressure of 10−13 atm and a temperature of 300 K, we can use the Ideal Gas Law, which is given by the equation:
PV=nRT
Where:
- P = pressure (in Pascals)
- V = volume (in cubic meters)
- n = number of moles
- R = universal gas constant (8.314J/(mol K))
- T = temperature (in Kelvin)
Step 1: Convert the pressure from atm to Pascals
Given:
P=10−13atm
To convert atm to Pascals, we use the conversion factor:
1atm=1.01×105Pa
Thus,
P=10−13atm×1.01×105Pa/atm=1.01×10−8Pa
Step 2: Convert the volume from cm³ to m³
Given:
V=1cm3
To convert cm³ to m³, we use the conversion:
1cm3=10−6m3
Thus,
V=1cm3=10−6m3
Step 3: Use the Ideal Gas Law to find the number of moles n
Rearranging the Ideal Gas Law to solve for n:
n=PVRT
Substituting the values we have:
- P=1.01×10−8Pa
- V=10−6m3
- R=8.314J/(mol K)
- T=300K
n=(1.01×10−8)×(10−6)(8.314)×(300)
Calculating the denominator:
8.314×300=2494.2J/mol
Now substituting back:
n=1.01×10−142494.2≈4.05×10−18mol
Step 4: Convert moles to molecules
To find the number of molecules, we use Avogadro's number (NA=6.022×1023molecules/mol):
Number of molecules=n×NA
Number of molecules=(4.05×10−18)×(6.022×1023)≈2.44×106
Final Answer
The number of molecules present in a volume of 1 cm³ at a pressure of 10−13 atm and a temperature of 300 K is approximately:
2.44×106
- P = pressure (in Pascals)
- V = volume (in cubic meters)
- n = number of moles
- R = universal gas constant (8.314J/(mol K))
- T = temperature (in Kelvin)
Given:
P=10−13atm
1atm=1.01×105Pa
P=10−13atm×1.01×105Pa/atm=1.01×10−8Pa
Given:
V=1cm3
1cm3=10−6m3
V=1cm3=10−6m3
Rearranging the Ideal Gas Law to solve for n:
n=PVRT
- P=1.01×10−8Pa
- V=10−6m3
- R=8.314J/(mol K)
- T=300K
8.314×300=2494.2J/mol
n=1.01×10−142494.2≈4.05×10−18mol
To find the number of molecules, we use Avogadro's number (NA=6.022×1023molecules/mol):
Number of molecules=n×NA
Number of molecules=(4.05×10−18)×(6.022×1023)≈2.44×106
The number of molecules present in a volume of 1 cm³ at a pressure of 10−13 atm and a temperature of 300 K is approximately:
2.44×106
Topper's Solved these Questions
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 More Than One Correct
7 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 2 Subjective
9 Videos
- THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY,THERMAL EXPANSION & KINETIC THEORY OF GASESEXERCISE - Level 1 Subjective
48 Videos
- THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESBOOK - DC PANDEY ENGLISHCHAPTER - THERMOMETRY THERMAL EXPANSION AND KINETIC THEORY OF GASESEXERCISE - Medical entrance gallary
30 Videos
- UNIT AND DIMENSIONSBOOK - DC PANDEY ENGLISHCHAPTER - UNIT AND DIMENSIONSEXERCISE - Assertion And Reason
2 Videos
Similar Questions
A chamber containing a gas was evacuated till the vacuum attained was 10−14 m of Hg. If the temperature of the chamber was 30∘C, the number of molecules that remains in it per cubic metre is
View SolutionA diatomic molecule X2 has a body- centred cubic (bcc) structure with a cell edge of 300pm. The density of the molecuel is 6.17gcm−3. The number of molecules present in 200 g of X2 is :
(Avogadroconstant (NA)=6×1023mol−1)
View SolutionA vessel of volume 2000cm3 contains 0.1mol of oxygen and 0.2mol of carbon dioxide. If the temperature of the mixture is 300K, find its pressure.
View SolutionThe highest vacuum attained so far is of the order of 10−11 mm of mercury. How many molecules are there in 1 cc of a vessel under such a high vacuum at 0∘C ?
View SolutionThe enthalpy of a system increases by 50 kJ when its internal energy is increased by 113 kJ. What is the pressure in kNm−2 of the system if the volume of gas is reduced by 103m3 at constant pressure?
View SolutionThe figure given below shows three glass chambers that are connected by valves of negligible volume. At the outset of an experiment, the valves are closed and the chambers contain the gases as detailed in the diagram. All the chambers are at the temperature of 300K and external pressure of 1.0atm.
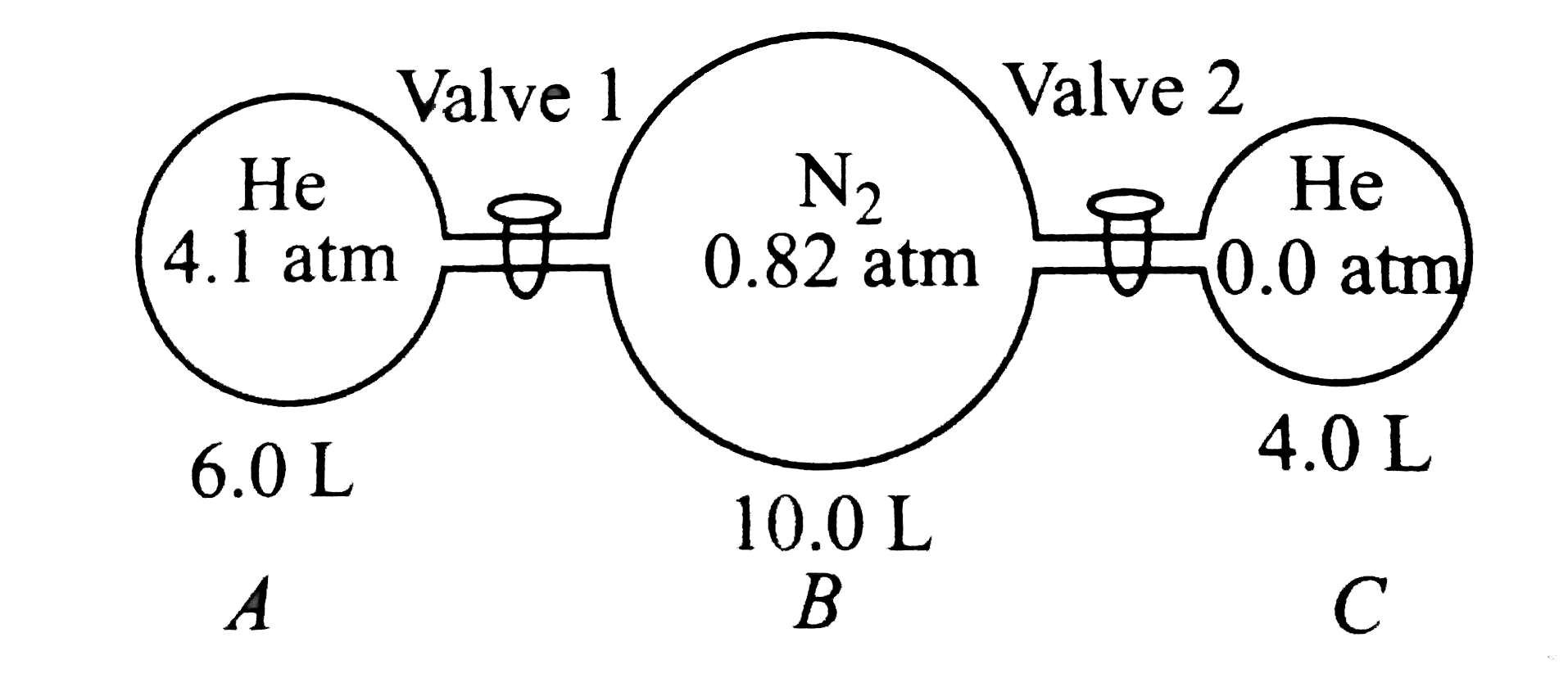
Which of the following represents the total kinetic energy of all the gas molecules after both valves are opened?
(R=0.082atmLK−1mol−1=8.314JK_1mol−1)
View SolutionA bulb A containing gas at 1.5 bar pressure was connected to an evacuated vessel of 1.0 dm3 capacity through a stopcock. The final pressure of the system dropped to 920 mbar at the same temperature. What is the volume of the container A?
View SolutionOne mole of an ideal monoatomic gas expands isothermally against constant external pressure of 1 atm from initial volume of 1l to a state where its final pressure becomes equal to external pressure. If initial temperature of gas is 300K then total entropy change of system in the above process is: [R =0.082L atm mol−1K−1=8.3Jmol−1K−1]
View SolutionOne mole of an ideal monoatomic gas expands isothermally against constant external pressure of 1atm from intial volume of 1L to a state where its final pressure becomes equal to external pressure. If initial temperature of gas in 300K then total entropy change of system in the above process is:
[R=0.0082Latmmol−1K−1=8.3Jmol−1K−1]
View SolutionThe volume of a gas in discharge tube is 1.12×10−7 ml, at 0∘C and 1 atm. The number of molecule of gas in the tube is-
View Solution
