In a process, the pressure of an ideal gas is proportional to square of the volume of the gas. If the temperature of the gas increases in this process, then work done by this gas
(a) is positive
(b) is negative
(c) is zero
(d) may be positive or negative
The correct Answer is:A
To solve the problem step by step, we will analyze the relationship between pressure, volume, and temperature for an ideal gas, and then determine the work done by the gas.
Step 1: Understand the relationship given in the problem
The problem states that the pressure (P) of an ideal gas is proportional to the square of its volume (V). This can be expressed mathematically as:
P∝V2
This implies that:
P=kV2
where k is a proportionality constant.
Step 2: Use the Ideal Gas Law
The ideal gas law states:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of the gas
- R = universal gas constant
- T = temperature
Step 3: Substitute the expression for pressure into the ideal gas law
Substituting P=kV2 into the ideal gas law gives:
kV2V=nRT
This simplifies to:
kV3=nRT
Step 4: Relate temperature to volume
From the equation kV3=nRT, we can express temperature as:
T=kV3nR
This shows that temperature is directly proportional to the cube of the volume:
T∝V3
Step 5: Analyze the effect of increasing temperature
If the temperature T increases, it follows from the relationship T∝V3 that the volume V must also increase.
Step 6: Determine the work done by the gas
The work done W by an expanding gas is given by the formula:
W=∫PdV
Since we have established that P=kV2, we can substitute this into the work formula:
W=∫kV2dV
This integral will yield a positive value since the volume is increasing.
Conclusion
Since the volume of the gas is increasing as the temperature increases, the work done by the gas is positive.
Final Answer:
The work done by the gas is positive.
---
The problem states that the pressure (P) of an ideal gas is proportional to the square of its volume (V). This can be expressed mathematically as:
P∝V2
This implies that:
P=kV2
where k is a proportionality constant.
The ideal gas law states:
PV=nRT
where:
- P = pressure
- V = volume
- n = number of moles of the gas
- R = universal gas constant
- T = temperature
Substituting P=kV2 into the ideal gas law gives:
kV2V=nRT
This simplifies to:
kV3=nRT
From the equation kV3=nRT, we can express temperature as:
T=kV3nR
This shows that temperature is directly proportional to the cube of the volume:
T∝V3
If the temperature T increases, it follows from the relationship T∝V3 that the volume V must also increase.
The work done W by an expanding gas is given by the formula:
W=∫PdV
Since we have established that P=kV2, we can substitute this into the work formula:
W=∫kV2dV
This integral will yield a positive value since the volume is increasing.
Since the volume of the gas is increasing as the temperature increases, the work done by the gas is positive.
The work done by the gas is positive.
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Objective Questions
1 Video
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Subjective
24 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Assertion And Reason
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
In a process the pressure of a gas is inversely proportional to the square of the volume. If temperature of the gas increases, then work done by the gas:
View SolutionIn a process the pressure of a gas is inversely proportional to the square of the volume. If temperature of the gas increases, then work done by the gas:
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the square of its absolute temperature. The γ for the gas is
View SolutionA sample of gas is going through cyclic process, work done by gas is
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to cube of its absolute temperature. The poision's ratio of gas is:
View SolutionIn a thermodynamic process two moles of a monatomic ideal gas obeys PV–2=constant. If temperature of the gas increases from 300 K to 400 K, then find work done by the gas (Where R = universal gas constant)
View SolutionThe thermodynamic process in which no work is done on or by the gas is
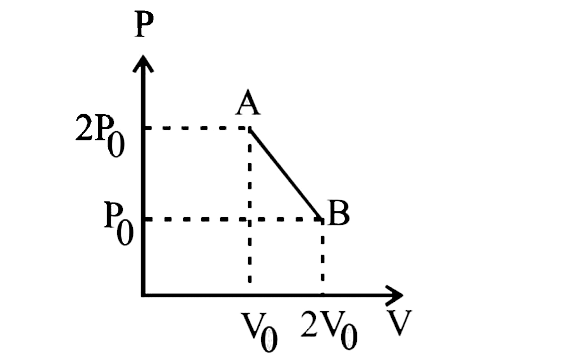
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will be:
View SolutionTemperature of 1mol of a gas is increased by 1∘ at constant pressure. The work done is
View SolutionTemperature of 1mol of a gas is increased by 1∘ at constant pressure. The work done is
View Solution