Three rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
The correct Answer is:A, B, C, D
To find the temperature of the junctions in the steady state for three rods with different thermal conductivities, we can follow these steps:
Step 1: Understand the Setup
We have three rods connected in series, each with the same length L and cross-sectional area A. The thermal conductivities of the rods are K, 2K, and 3K. The temperatures at the ends of the rods are TA=200∘C and TB=100∘C.
Step 2: Define the Temperatures at Junctions
Let the temperatures at the junctions be θ1 (between the first and second rod) and θ2 (between the second and third rod). We need to find θ1 and θ2.
Step 3: Apply the Heat Transfer Formula
The heat transfer H through each rod can be expressed as:
H=kA(TA−θ1)L(for rod 1)
H=2kA(θ1−θ2)L(for rod 2)
H=3kA(θ2−TB)L(for rod 3)
Step 4: Set Up the Heat Transfer Equations
Since the heat transfer through each rod is equal in steady state, we can equate the expressions:
K(TA−θ1)L=2K(θ1−θ2)L=3K(θ2−TB)L
We can cancel K and L from all terms, leading to:
TA−θ1=2(θ1−θ2)=3(θ2−TB)
Step 5: Solve for θ1
From the first equation:
TA−θ1=2(θ1−θ2)
Rearranging gives:
TA−θ1=2θ1−2θ2
TA+θ2=3θ1
θ1=TA+θ23
Step 6: Solve for θ2
From the second equation:
2(θ1−θ2)=3(θ2−TB)
Rearranging gives:
2θ1−2θ2=3θ2−3TB
2θ1+3TB=5θ2
θ2=2θ1+3TB5
Step 7: Substitute and Solve
Now we have two equations:
1. θ1=TA+θ23
2. θ2=2θ1+3TB5
Substituting θ2 from the second equation into the first:
θ1=TA+2θ1+3TB53
Multiply through by 15 to eliminate the fractions:
15θ1=5TA+2θ1+3TB
Rearranging gives:
13θ1=5TA+3TB
θ1=5TA+3TB13
Substituting TA=200∘C and TB=100∘C:
θ1=5(200)+3(100)13=1000+30013=130013≈100∘C
Step 8: Find θ2
Now substitute θ1 back into the equation for θ2:
θ2=2(θ1)+3TB5=2(100)+3(100)5=200+3005=5005=100∘C
Final Results
The temperatures at the junctions are:
- θ1≈145.5∘C
- θ2≈118.2∘C
We have three rods connected in series, each with the same length L and cross-sectional area A. The thermal conductivities of the rods are K, 2K, and 3K. The temperatures at the ends of the rods are TA=200∘C and TB=100∘C.
Let the temperatures at the junctions be θ1 (between the first and second rod) and θ2 (between the second and third rod). We need to find θ1 and θ2.
The heat transfer H through each rod can be expressed as:
H=kA(TA−θ1)L(for rod 1)
H=2kA(θ1−θ2)L(for rod 2)
H=3kA(θ2−TB)L(for rod 3)
Since the heat transfer through each rod is equal in steady state, we can equate the expressions:
K(TA−θ1)L=2K(θ1−θ2)L=3K(θ2−TB)L
We can cancel K and L from all terms, leading to:
TA−θ1=2(θ1−θ2)=3(θ2−TB)
From the first equation:
TA−θ1=2(θ1−θ2)
Rearranging gives:
TA−θ1=2θ1−2θ2
TA+θ2=3θ1
θ1=TA+θ23
From the second equation:
2(θ1−θ2)=3(θ2−TB)
Rearranging gives:
2θ1−2θ2=3θ2−3TB
2θ1+3TB=5θ2
θ2=2θ1+3TB5
Now we have two equations:
1. θ1=TA+θ23
2. θ2=2θ1+3TB5
θ1=TA+2θ1+3TB53
Multiply through by 15 to eliminate the fractions:
15θ1=5TA+2θ1+3TB
Rearranging gives:
13θ1=5TA+3TB
θ1=5TA+3TB13
Substituting TA=200∘C and TB=100∘C:
θ1=5(200)+3(100)13=1000+30013=130013≈100∘C
Now substitute θ1 back into the equation for θ2:
θ2=2(θ1)+3TB5=2(100)+3(100)5=200+3005=5005=100∘C
The temperatures at the junctions are:
- θ1≈145.5∘C
- θ2≈118.2∘C
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Assertion And Reason
10 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 1 Objective
11 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Exercise 22.1
7 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
Three rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
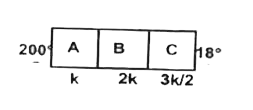
View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionA composite rod made of three rods of equal length and cross-section as shown in fig. The thermal conductivites of the materials of the rods are K/2, 5K and K respectively. The end A and end B are at constant tempertures. All heat entering the face A goes out of the end B there being no loss of heat from the sides of the bar. The effective thermal conductivity of the bar is

View Solution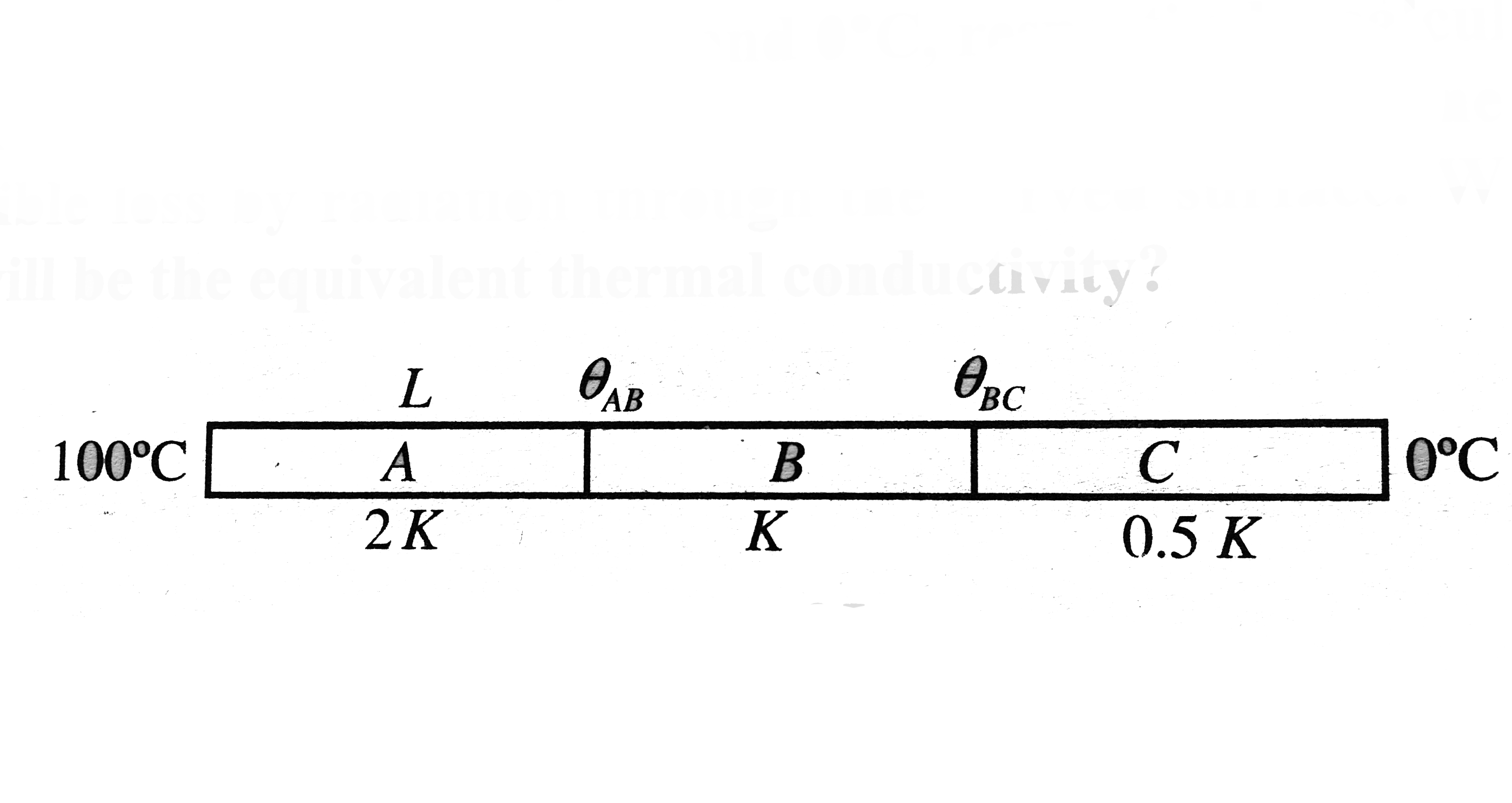
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
View Solution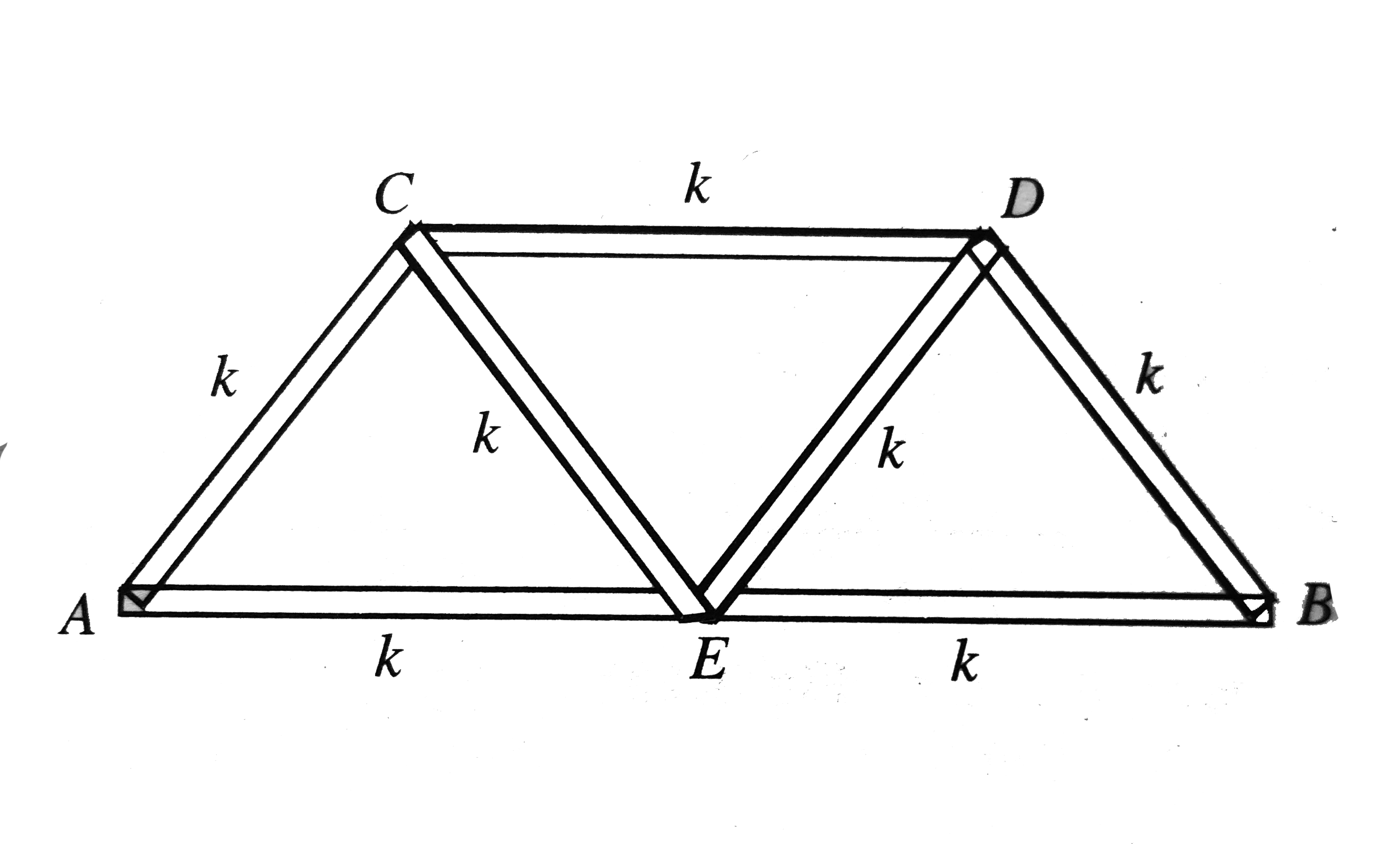
Seven identical rods of material of thermal conductivity k are connected as shown in Fig. All the rods are of identical length l and cross sectional area A If the one end A is kept at 100∘C and the other end is kept at 0∘C what would be the temperatures of the junctions C, D and E(θC,θ)D and θE) in the steady state?
View Solution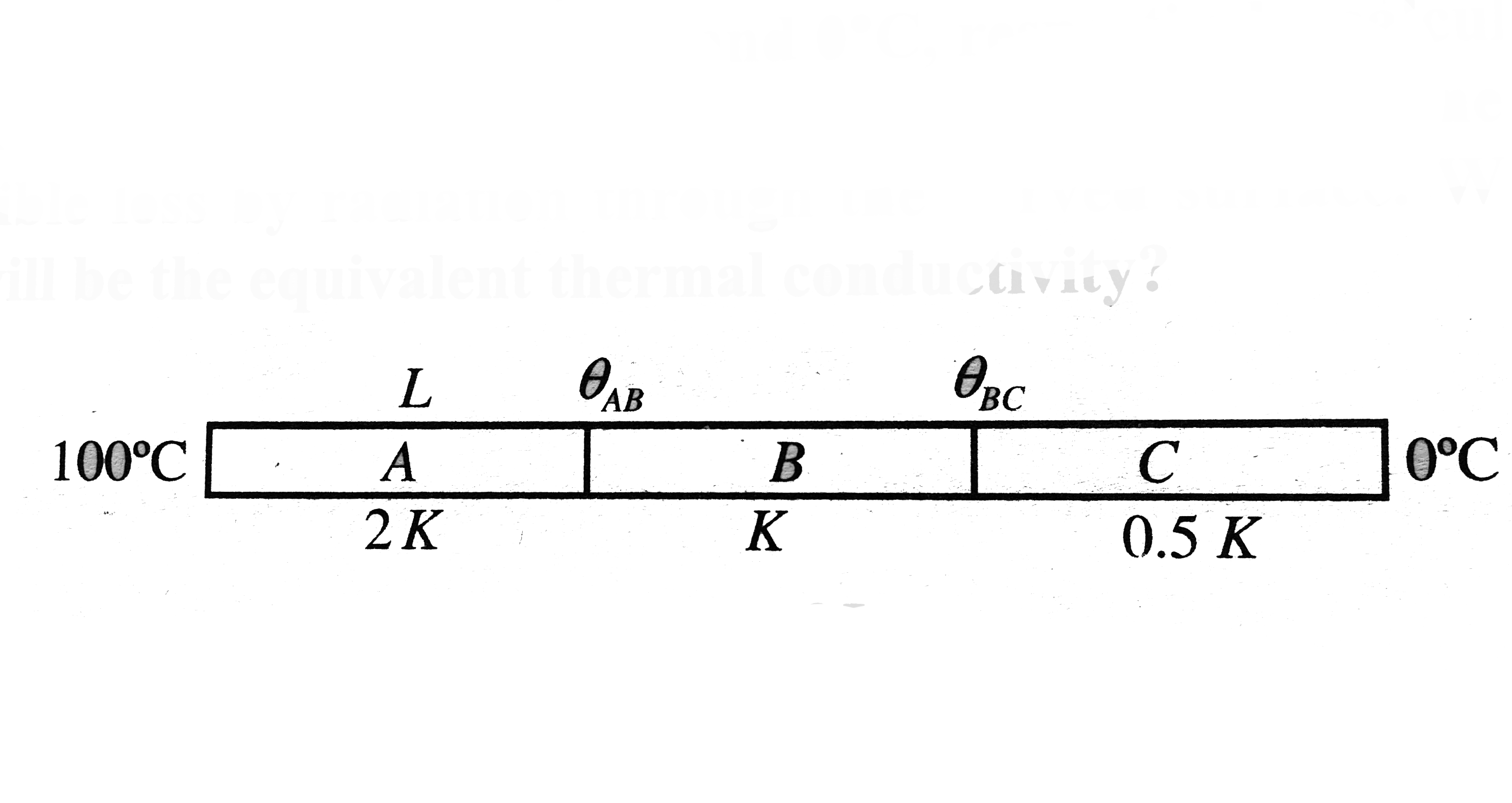
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. Assume negligible loss by radiation through the curved surface. What will be the equivalent thermal conductivity?
View SolutionThree bars of equal lengths and equal areas of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and last bars are at temperatures 20∘Cand18∘C respectively in the steady state calculate the temperature of both the junctions.
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is

View Solution
A circular ring (centre O) of radius a, and of uniform cross section is made up of three different metallic rods AB, BC and CA (joined together at the points A, B and C in pairs) of thermal conductivityies α1,α2 and α3 respectively (see diagram). The junction A, B and C are maintained at the temperatures 100∘C,50∘C and 0∘C, respectively. All the rods are of equal lengths and cross sections. Under steady state conditions, assume that no heat is lost from the sides of the rods. Let Q1,Q2 and Q3 be the rates of transmission of heat along the three rods AB, BC and CA. Then
View Solution
A circular ring (centre O) of radius a, and of uniform cross section is made up of three different metallic rods AB, BC and CA (joined together at the points A, B and C in pairs) of thermal conductivityies α1,α2 and α3 respectively (see diagram). The junction A, B and C are maintained at the temperatures 100∘C,50∘C and 0∘C, respectively. All the rods are of equal lengths and cross sections. Under steady state conditions, assume that no heat is lost from the sides of the rods. Let Q1,Q2 and Q3 be the rates of transmission of heat along the three rods AB, BC and CA. Then
View Solution
