Using the concept of energy density, find the total energy stored in a
a. parallel plate capacitor
b. charged spherical conductor.
To find the total energy stored in a parallel plate capacitor and a charged spherical conductor using the concept of energy density, we can follow these steps:
Part A: Energy Stored in a Parallel Plate Capacitor
1. Understand Energy Density: The energy density (u) in an electric field is given by the formula:
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field.
2. Electric Field in a Parallel Plate Capacitor: The electric field (E) between the plates of a parallel plate capacitor is uniform and can be expressed as:
E=σϵ0
where σ is the surface charge density (charge per unit area).
3. Volume of the Capacitor: The volume (V) between the plates can be calculated as:
V=A⋅d
where A is the area of one of the plates and d is the separation between the plates.
4. Total Energy Stored: The total energy (U) stored in the capacitor can be calculated by multiplying the energy density by the volume:
U=u⋅V=12ϵ0E2⋅(A⋅d)
5. Substituting Electric Field: Substitute E=σϵ0 into the energy expression:
U=12ϵ0(σϵ0)2⋅(A⋅d)
6. Relate Charge and Surface Charge Density: The surface charge density σ can be expressed in terms of charge Q:
σ=QA
Substitute this into the energy expression:
U=12ϵ0(Q/Aϵ0)2⋅(A⋅d)
7. Simplifying: After simplification, we find:
U=Q22C
where C=ϵ0Ad is the capacitance of the parallel plate capacitor.
Part B: Energy Stored in a Charged Spherical Conductor
1. Electric Field of a Charged Sphere: For a charged spherical conductor, the electric field at a distance r from the center is given by:
E=kQr2
where k is Coulomb's constant.
2. Energy Density: The energy density in the electric field is still given by:
u=12ϵ0E2
3. Volume Element: Consider a thin spherical shell of radius r and thickness dr. The volume (dV) of this shell is:
dV=4πr2dr
4. Total Energy: The total energy stored in the electric field outside the sphere can be calculated by integrating the energy density over the volume:
U=∫udV=∫12ϵ0E2⋅4πr2dr
5. Substituting Electric Field: Substitute E=kQr2:
U=∫12ϵ0(kQr2)2⋅4πr2dr
6. Integrating: This simplifies to:
U=2πk2Q2ϵ0∫1r2dr
The limits of integration are from the radius of the sphere R to infinity.
7. Final Calculation: After integrating, we find:
U=kQ22R
Summary of Results
- Energy Stored in Parallel Plate Capacitor:
U=Q22C
- Energy Stored in Charged Spherical Conductor:
U=kQ22R
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field.
E=σϵ0
where σ is the surface charge density (charge per unit area).
V=A⋅d
where A is the area of one of the plates and d is the separation between the plates.
U=u⋅V=12ϵ0E2⋅(A⋅d)
U=12ϵ0(σϵ0)2⋅(A⋅d)
σ=QA
Substitute this into the energy expression:
U=12ϵ0(Q/Aϵ0)2⋅(A⋅d)
U=Q22C
where C=ϵ0Ad is the capacitance of the parallel plate capacitor.
E=kQr2
where k is Coulomb's constant.
u=12ϵ0E2
dV=4πr2dr
U=∫udV=∫12ϵ0E2⋅4πr2dr
U=∫12ϵ0(kQr2)2⋅4πr2dr
U=2πk2Q2ϵ0∫1r2dr
The limits of integration are from the radius of the sphere R to infinity.
U=kQ22R
- Energy Stored in Parallel Plate Capacitor:
U=Q22C
- Energy Stored in Charged Spherical Conductor:
U=kQ22R
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Deduce an expression for the potential energy stored in a parallel plate capacitor.
View SolutionFind the total energy stored in the capacitors in the given network.
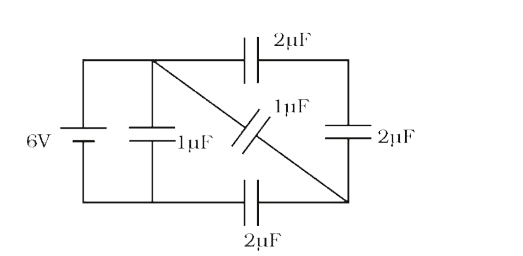
View SolutionFind the charge stored in the capacitor.
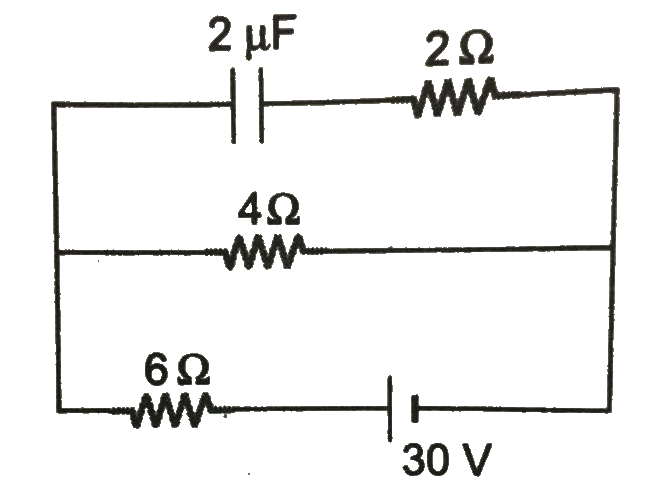
View SolutionFind the charge stored in the capacitor.
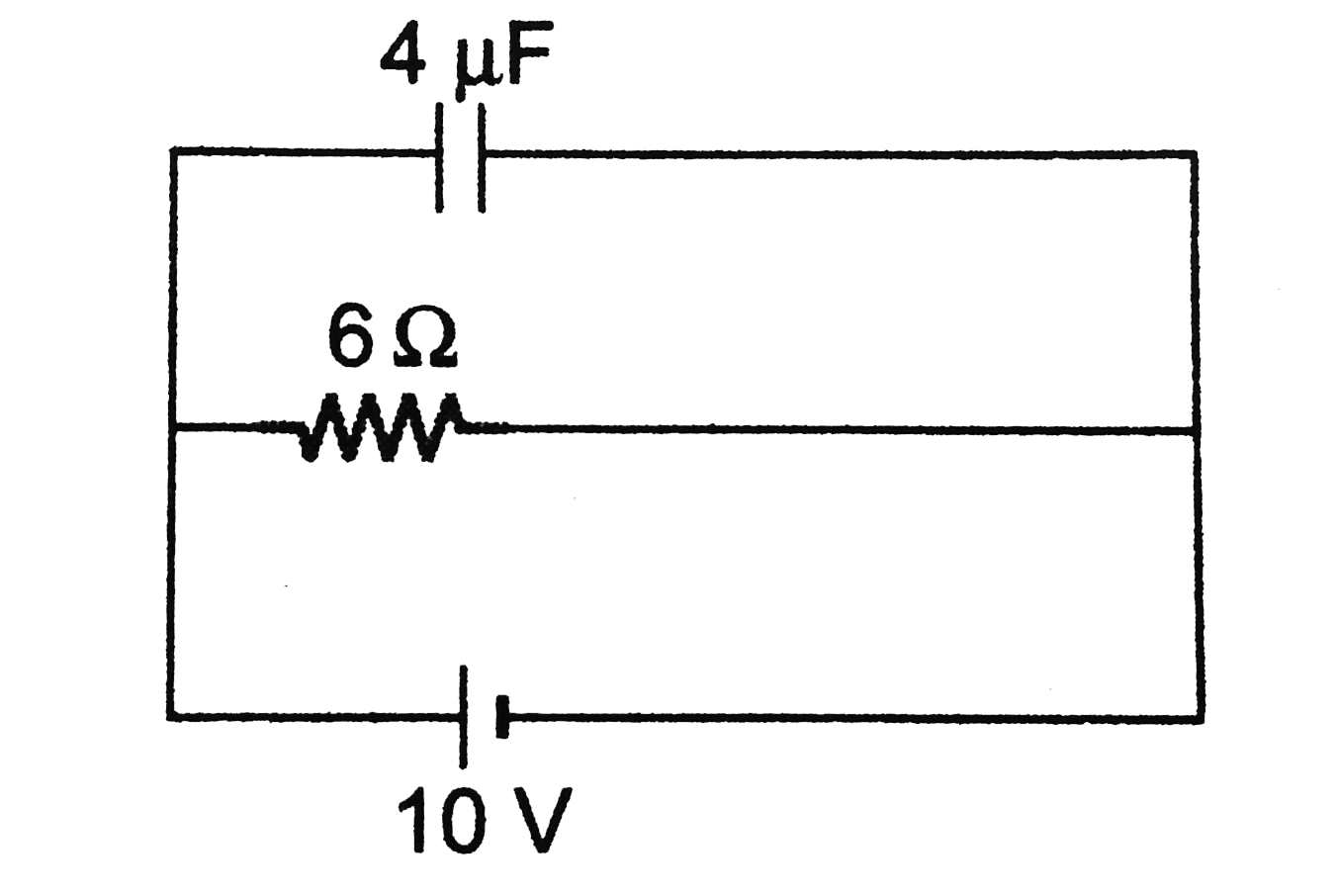
View SolutionFind the charge stored in the capacitor.
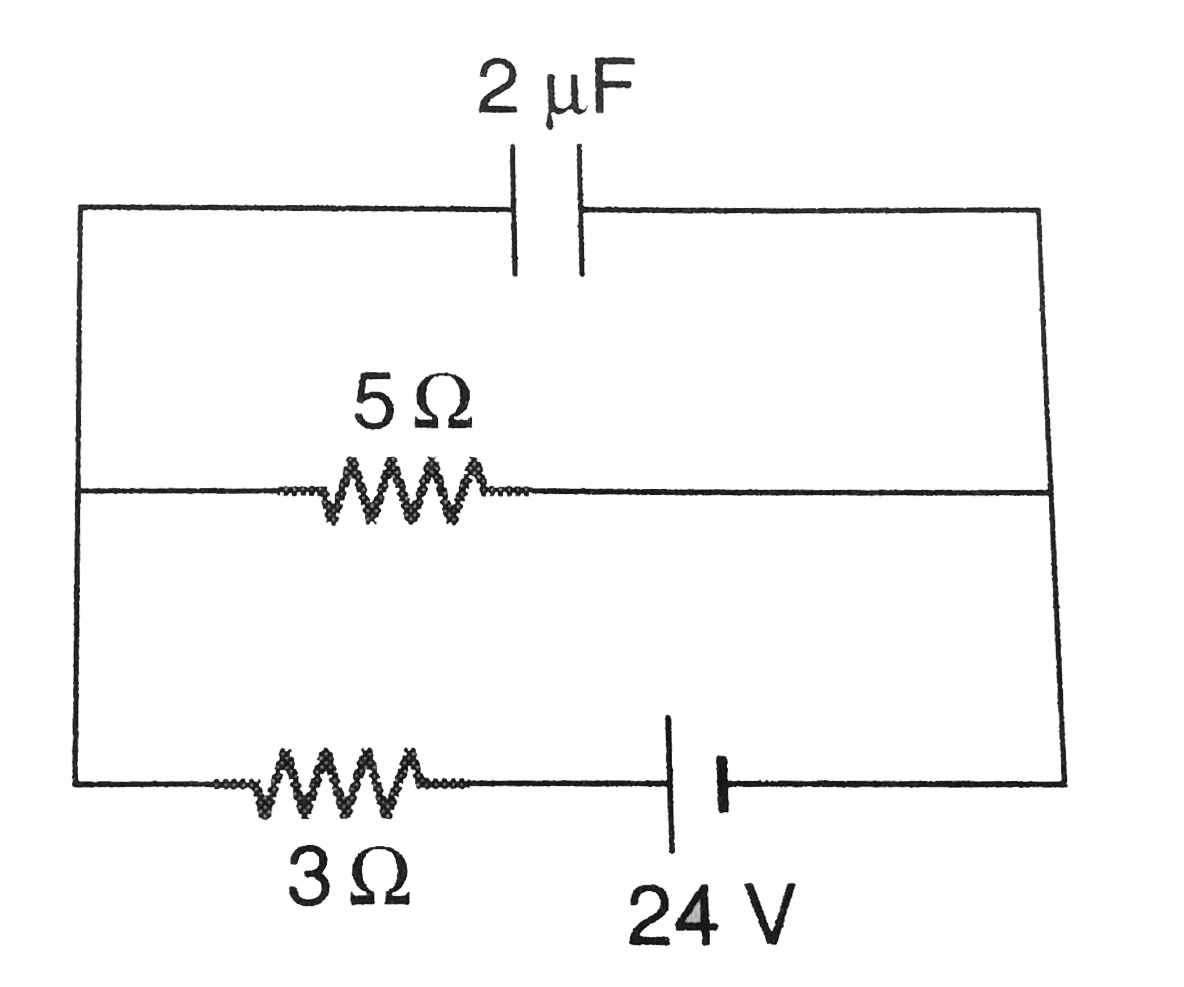
View SolutionUsing the concept of energy density , show that the total energy stored by a shell of radius R and charge Q is Q28πε0R
View SolutionThe total electrostatic energy stored in both the capacitor is
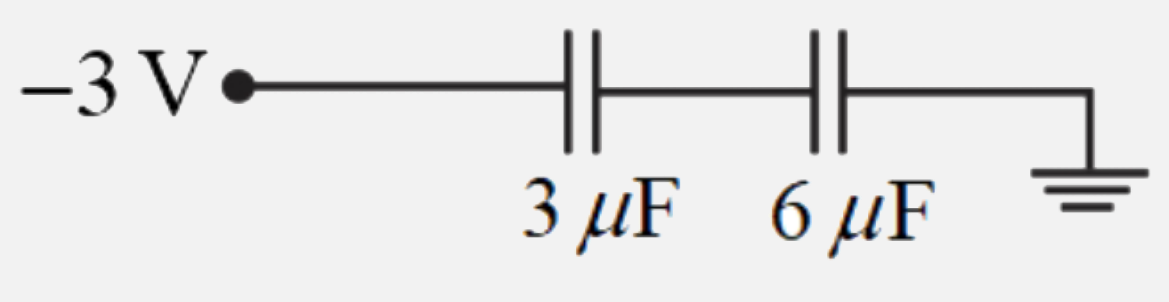
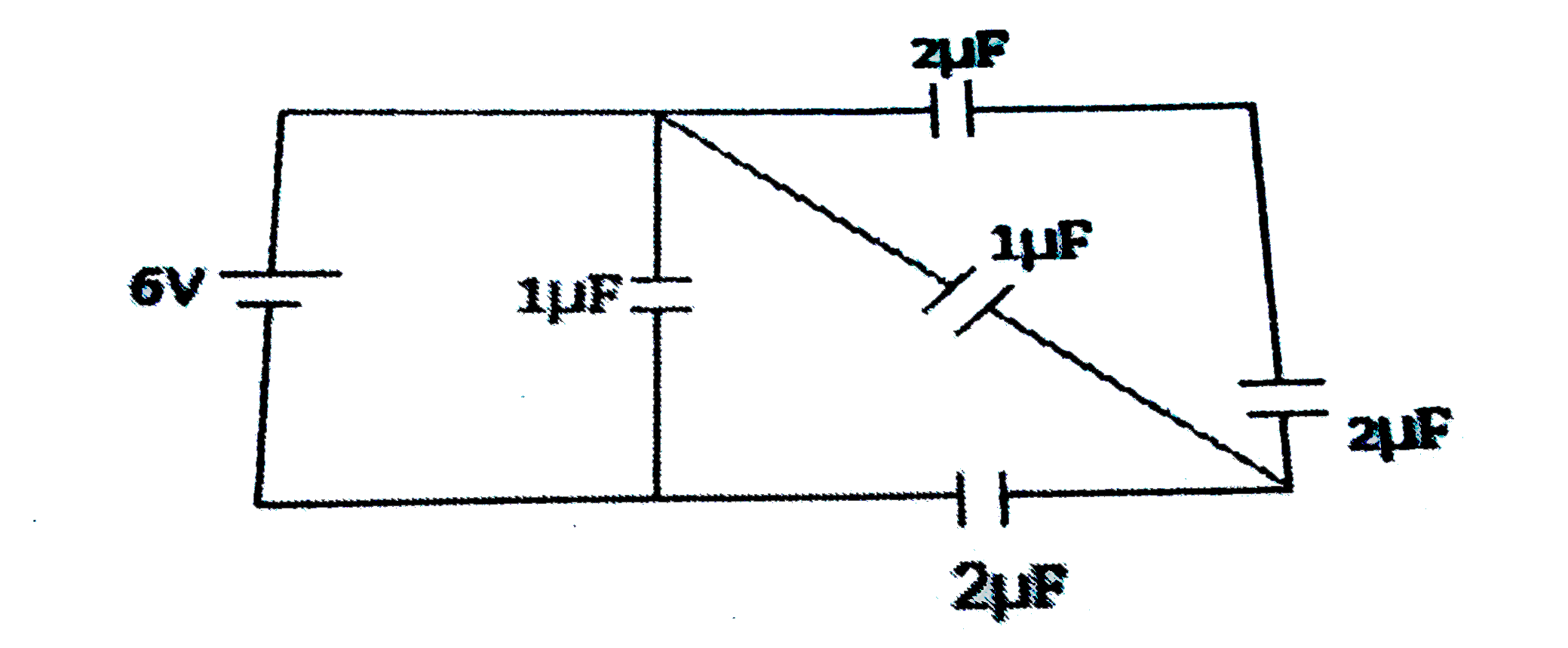
View SolutionFind total energy stored in capacitors given in the circuit
View SolutionAnswer the following:
(a) Describe briefly the process of transferring charge between the two plates of a parallel plate capacitor when connected to a battery. Derive an expression for the energy stored in a capacitor.
(b) A parallel plate capacitor is connected to a battery of potential difference V. It is disconnected from battery and then connected to another uncharged capacitor of the same capacitance. Calculate the ratio of the energy stored in the combination to the initial energy on the single capacitor.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View Solution
