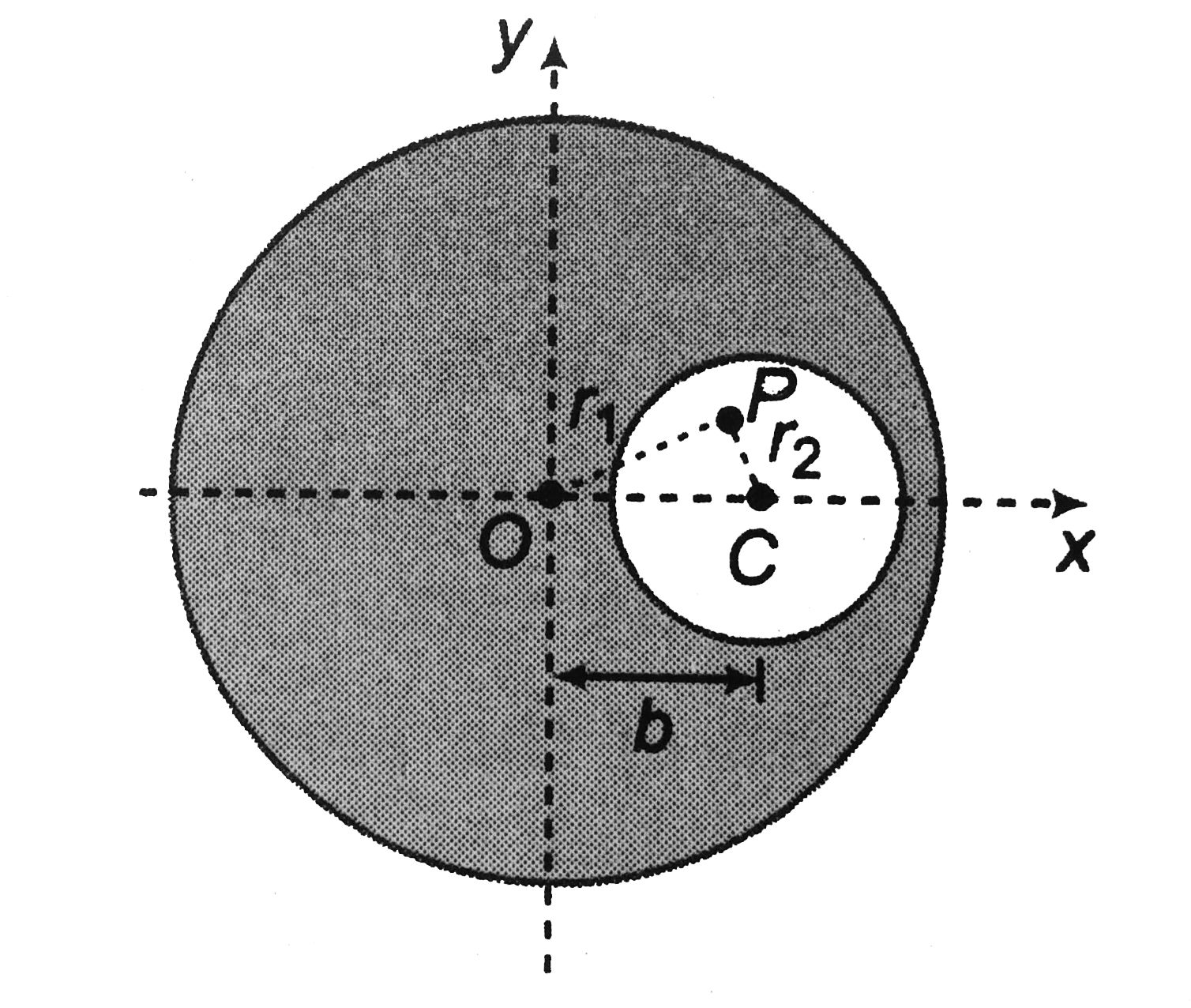
A current is passing through a cylindrical conductor with a hole (or cavity) inside it. Show that the magnetic field inside the hole is uniform and find its magnitude and direction.

Video Solution

Text Solution

Verified by Experts

Let us find the magnetic field at point P inside the cavity at a distace $r_{1}$ and ) and $r_{2}$ from C.
$J = current per unit area$
$R = radius of cylinder$
$a = radius of cavity$
$i_{1}$ whole current from cylinder $= J (π r^{2})$
$i_{2} =$ curent from hole $= J (π a^{2})$

At point $P$ magnetic field due to $i_{1}$ is $B_{1}$ (perpendicular to $O P$ ) and is $B_{2}$ due to $i_{2}$ (perpedicular to CP) in the directions shown. Although $B_{1}$ and $B_{2}$ are actually at P, but for better
understanding theey are drawnn at $O$ and $C$ respectively. Let $B_{x}$ be the x-coponent of resultant of $B_{1}$ and $B_{2}$ and $B_{y}$ its y-component. then
$B_{x} = B_{1} sin α - B_{2} sin β$
$= (\frac{μ_{0}}{2 π} \frac{i_{1}}{R^{2}} r_{1}) sin α - (\frac{μ_{0}}{2 π} \frac{i_{2}}{α^{2}} . r_{2}) sin β$
$= (\frac{μ_{0}}{2 π} \frac{J π R^{2}}{R^{2}} . r_{1} sin α) - (\frac{μ_{0}}{2 π} \frac{J . π a^{2}}{a^{2}} r_{2} sin β)$
$\frac{μ_{0} J}{2} (r_{1} sin α - r_{2} sin β) = 0$
Because in $△ O P C \frac{r_{1}}{sin β} = \frac{r_{2}}{sin α} = h or r_{1} sin α - r_{2} sin β = 0$
$N o w, B_{y} = - (B - 1 cos α + B_{2} cos b e t)$
$= - \frac{μ_{0} J}{2} (r_{1} cos α + r_{2} cos β)$
From $△ O P C, we can see that$
$r_{1} cos α + r_{2} cos β = b or B_{y} = - \frac{μ_{0} J b}{2} =$ constant

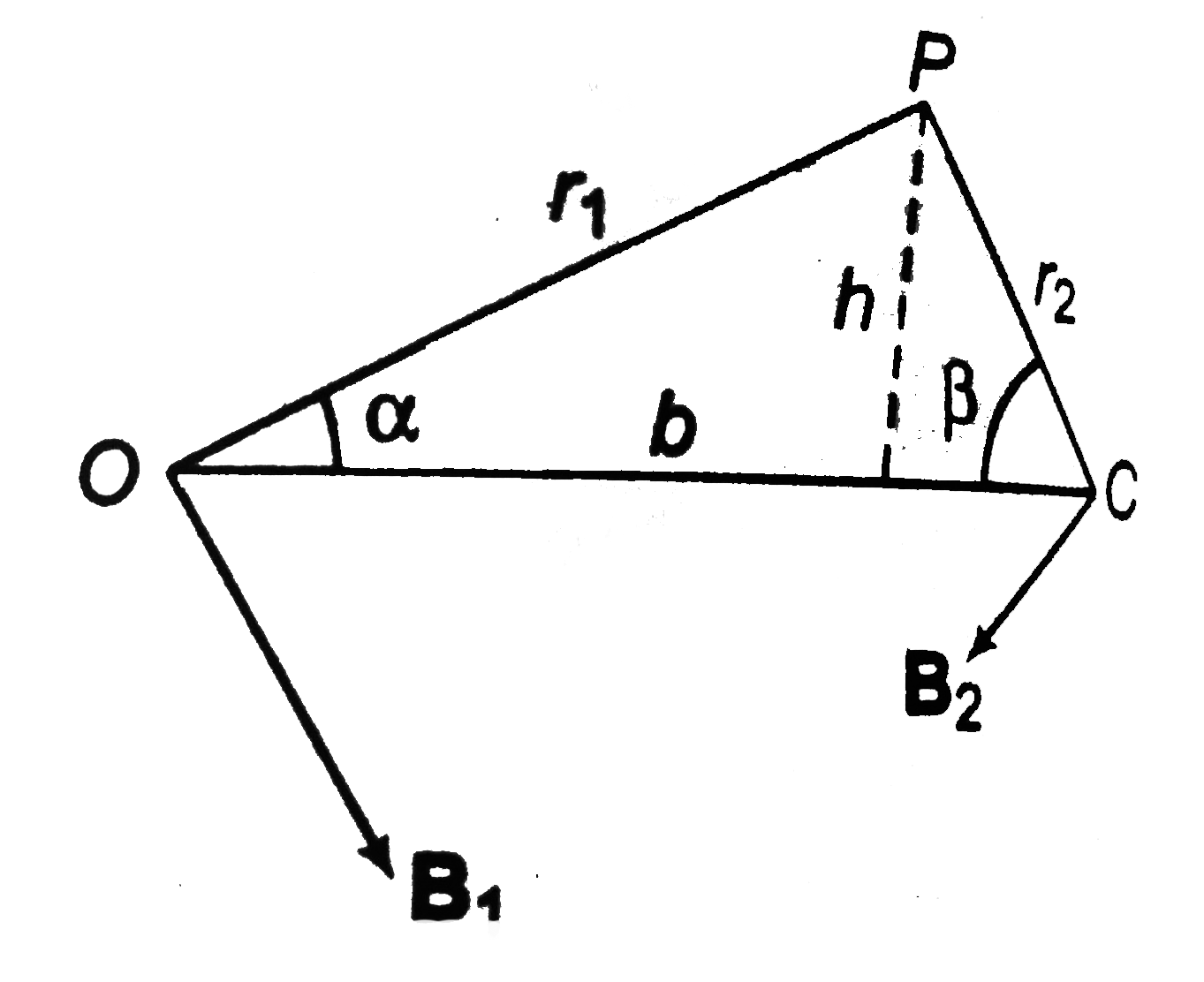
Thus we can see that net magnetic field at point $P$ is along negative y-direction and constant in magnitude.

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Current flowing through a long solenoid is varied. Then, magnetic flux density of the magnetic field inside it varies :
Ainversely with I
Binversely with $I^{2}$
Cdirectly with I
Ddirectly with $I^{2}$

DC PANDEY ENGLISH-MAGNETICS-MCQ_TYPE

Home
Ask Doubt
Profile