An object 6.0 mm is placed 16.5 cm to the left of the vertex of a concave spherical mirror having
a radius of curvature of 22.0 cm.
(a) Draw principal ray diagram showing formation of the image.
(b) Determine the position, size, orientation, and nature (real or virtual) of the image.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the given data
- Object height (h) = 6.0 mm = 0.6 cm (convert to cm for consistency)
- Object distance (u) = -16.5 cm (negative because the object is on the same side as the incoming light)
- Radius of curvature (R) = 22.0 cm
Step 2: Calculate the focal length (F)
The focal length (F) of a concave mirror is given by the formula:
F=R2
Substituting the given radius of curvature:
F=22.0 cm2=11.0 cm
Step 3: Use the mirror formula to find the image distance (v)
The mirror formula is:
1F=1v+1u
Rearranging gives:
1v=1F−1u
Substituting the values:
1v=111.0−1−16.5
Calculating:
1v=111.0+116.5
Finding a common denominator and calculating:
1v=16.5+11.011.0×16.5=27.5181.5
So,
v=181.527.5≈6.6 cm
Step 4: Determine the nature of the image
Since the value of v is positive, the image is formed on the same side as the object, indicating that it is a real image.
Step 5: Calculate the magnification (m)
The magnification (m) is given by:
m=−vu
Substituting the values:
m=−6.6−16.5=0.4
Step 6: Determine the size of the image (h')
The size of the image can be calculated using:
m=h′h
Where h is the height of the object. Rearranging gives:
h′=m×h
Substituting the values:
h′=0.4×0.6 cm=0.24 cm
Step 7: Summarize the results
- Position of the image (v): 6.6 cm (to the left of the mirror)
- Size of the image (h'): 0.24 cm
- Orientation: Since the magnification is positive, the image is upright.
- Nature of the image: Real and inverted.
- Object height (h) = 6.0 mm = 0.6 cm (convert to cm for consistency)
- Object distance (u) = -16.5 cm (negative because the object is on the same side as the incoming light)
- Radius of curvature (R) = 22.0 cm
The focal length (F) of a concave mirror is given by the formula:
F=R2
Substituting the given radius of curvature:
F=22.0 cm2=11.0 cm
The mirror formula is:
1F=1v+1u
Rearranging gives:
1v=1F−1u
Substituting the values:
1v=111.0−1−16.5
Calculating:
1v=111.0+116.5
Finding a common denominator and calculating:
1v=16.5+11.011.0×16.5=27.5181.5
So,
v=181.527.5≈6.6 cm
Since the value of v is positive, the image is formed on the same side as the object, indicating that it is a real image.
The magnification (m) is given by:
m=−vu
Substituting the values:
m=−6.6−16.5=0.4
The size of the image can be calculated using:
m=h′h
Where h is the height of the object. Rearranging gives:
h′=m×h
Substituting the values:
h′=0.4×0.6 cm=0.24 cm
- Position of the image (v): 6.6 cm (to the left of the mirror)
- Size of the image (h'): 0.24 cm
- Orientation: Since the magnification is positive, the image is upright.
- Nature of the image: Real and inverted.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Single Correct16videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 More Than One Correct6videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Objective12videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective21videos
REFRACTION OF LIGHT
Similar Questions
An object 9.0 mm tall is placed 12.0 cm to the left of the vertex of a convex spherical mirror
whose radius of curvature has a magnitude of 20.0 cm.
(a) Draw a principal ray diagram showing formation of the image.
(b) Determine the position, size, orientation, and nature (real or vertual) of the image.View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object 5 cm tall is placed 1 m from a concave spherical mirror which has a radius of curvature of 20 cm. The size of the image is
View SolutionAn object 2.5 cm high is placed at a distance of 10 cm from a concave mirror of radius of curvature 30 cm The size of the image is
View SolutionFig. shows a concave mirror with its pole at P, focus F and centre of curvature C. Draw ray diagram to show the formation of image of an object OA.
 View Solution
View SolutionThe co-ordinates of the image of point object P formed by a concave mirror of radius of curvature 20 cm (consider paraxial rays only ) as shown in the figure is
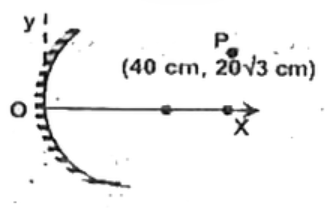 View Solution
View SolutionAn object is placed at 4 cm distance in front of a concave mirror of radius of curvature 24 cm. Find the position of image. Is the image magnified?
View SolutionAn object is placed at 6 cm distance in front of a concave mirror of focal length 4 cm.
What will be the nature of the image?View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View Solution

