Question

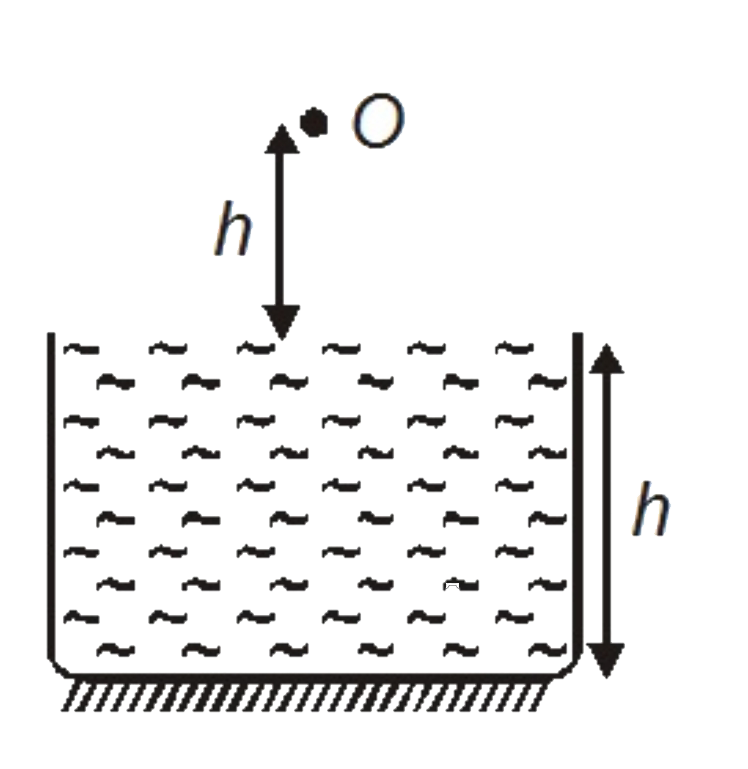
A bird is flying over a swimming pool at a height of $2m$ from the water surface. If the bottom is perfectly plane reflecting surface and depth of swimming pool is $1m,$ then the distance of final image of bird from the bird itself is ${\mu }_w=4/3$

Options

A. (A) `11/3 m`
B. (B) `23/3 m`
C. (C) `11/4 m`
D. (D) `11/2 m`

Answer

D

Explanation

To find the distance of the final image of the bird from the bird itself, we can break down the problem into several steps.

1. Identify the Given Values:
- Height of the bird above the water surface, \( h = 2 \, \text{m} \)
- Depth of the swimming pool, \( d = 1 \, \text{m} \)
- Refractive index of water, \( \mu_w = \frac{4}{3} \)

2. Calculate the Apparent Height from the Water Surface:
- The apparent height of the bird when viewed from the water surface can be calculated using the formula:
\( h_{\text{apparent}} = h \times \mu_w \)
- Substituting the values:
\( h_{\text{apparent}} = 2 \times \frac{4}{3} = \frac{8}{3} \, \text{m} \)

3. Calculate the Total Distance from the Bottom of the Pool:
- Since the depth of the pool is \( 1 \, \text{m} \), the total distance from the bottom of the pool to the apparent height is:
\( h_{\text{total}} = h_{\text{apparent}} + d = \frac{8}{3} + 1 = \frac{8}{3} + \frac{3}{3} = \frac{11}{3} \, \text{m} \)

4. Calculate the Position of the Image:
- The image formed by the reflection at the bottom of the pool will be at the same distance below the bottom surface as the apparent height above the water surface:
\( h_{\text{image}} = h_{\text{total}} = \frac{11}{3} \, \text{m} \)

5. Calculate the Apparent Height After Refraction Back to Air:
- When light travels from water (denser medium) to air (rarer medium), the apparent height is calculated as:
\( h_{\text{apparent, final}} = \frac{h_{\text{image}}}{\mu_w} = \frac{\frac{11}{3}}{\frac{4}{3}} = \frac{11}{4} \, \text{m} \)

6. Calculate the Distance from the Bird to the Final Image:
- The distance from the bird (which is \( 2 \, \text{m} \) above the water surface) to the final image is:
\( \text{Distance} = h_{\text{apparent, final}} + h = \frac{11}{4} + 2 = \frac{11}{4} + \frac{8}{4} = \frac{19}{4} \, \text{m} \)
- Thus, the distance of the final image of the bird from the bird itself is:
\( \text{Distance} = \frac{19}{4} \, \text{m} \approx 4.75 \, \text{m} \)

Final Answer:
The distance of the final image of the bird from the bird itself is approximately \( 4.75 \, \text{m} \).