The energy levels of a hypothetical one electron atom are given by En=−18.0n2eV
where n = 1,2,3,…. (a) Compute the four lowest energy levels and construct the energy levels diagram. (b) What is the first excitation potential (c ) What wavelength (Å) can be emitted when these atoms in the ground state are bombarged by electrons that have been accelerated through a potential difference of 16.2 V? (e) what is the photoelectric threshold wavelength of this atom?
The correct Answer is:A, C, D
Let's break down the solution step by step for the given problem.
Part (a): Compute the four lowest energy levels and construct the energy levels diagram.
1. Energy Level Formula: The energy levels of the hypothetical one-electron atom are given by:
En=−18.0n2 eV
where n=1,2,3,…
2. Calculate the Energy Levels:
- For n=1:
E1=−18.012=−18.0 eV
- For n=2:
E2=−18.022=−18.04=−4.5 eV
- For n=3:
E3=−18.032=−18.09=−2.0 eV
- For n=4:
E4=−18.042=−18.016=−1.125 eV
3. Energy Level Diagram:
- Draw a vertical line representing energy levels.
- Label the levels as follows:
- E1=−18.0 eV
- E2=−4.5 eV
- E3=−2.0 eV
- E4=−1.125 eV
Part (b): What is the first excitation potential?
1. First Excitation Potential: The first excitation potential is the energy difference between the first and second energy levels:
Excitation Potential=E2−E1=(−4.5)−(−18.0)=13.5 eV
Part (c): What wavelength (Å) can be emitted when these atoms in the ground state are bombarded by electrons that have been accelerated through a potential difference of 16.2 V?
1. Energy of Accelerated Electrons: The energy gained by an electron when accelerated through a potential difference V is given by:
E=eV=16.2 eV
2. Possible Transitions:
- The maximum energy difference that can be achieved is E4−E1:
E4−E1=(−1.125)−(−18.0)=16.875 eV
- Since 16.875 eV>16.2 eV, transitions from n=1 to n=3 are possible.
3. Calculate Wavelengths:
- For λ32:
λ32=12375E3−E2=12375(−2.0)−(−4.5)=123752.5=4950 Å
- For λ31:
λ31=12375E3−E1=12375(−2.0)−(−18.0)=1237516.0=773 Å
- For λ21:
λ21=12375E2−E1=12375(−4.5)−(−18.0)=1237513.5=917 Å
Part (d): What is the photoelectric threshold wavelength of this atom?
1. Photoelectric Threshold Energy: The photoelectric threshold energy corresponds to the first excitation potential:
Ethreshold=13.5 eV
2. Calculate the Threshold Wavelength:
λthreshold=12375Ethreshold=1237513.5=915.74 Å
Summary of Answers:
- (a) Energy levels: E1=−18.0 eV,E2=−4.5 eV,E3=−2.0 eV,E4=−1.125 eV
- (b) First excitation potential: 13.5 eV
- (c) Wavelengths emitted: 4950 Å,773 Å,917 Å
- (d) Photoelectric threshold wavelength: 915.74 Å
En=−18.0n2 eV
where n=1,2,3,…
- For n=1:
E1=−18.012=−18.0 eV
- For n=2:
E2=−18.022=−18.04=−4.5 eV
- For n=3:
E3=−18.032=−18.09=−2.0 eV
- For n=4:
E4=−18.042=−18.016=−1.125 eV
- Draw a vertical line representing energy levels.
- Label the levels as follows:
- E1=−18.0 eV
- E2=−4.5 eV
- E3=−2.0 eV
- E4=−1.125 eV
Excitation Potential=E2−E1=(−4.5)−(−18.0)=13.5 eV
E=eV=16.2 eV
- The maximum energy difference that can be achieved is E4−E1:
E4−E1=(−1.125)−(−18.0)=16.875 eV
- Since 16.875 eV>16.2 eV, transitions from n=1 to n=3 are possible.
- For λ32:
λ32=12375E3−E2=12375(−2.0)−(−4.5)=123752.5=4950 Å
- For λ31:
λ31=12375E3−E1=12375(−2.0)−(−18.0)=1237516.0=773 Å
- For λ21:
λ21=12375E2−E1=12375(−4.5)−(−18.0)=1237513.5=917 Å
Ethreshold=13.5 eV
λthreshold=12375Ethreshold=1237513.5=915.74 Å
- (a) Energy levels: E1=−18.0 eV,E2=−4.5 eV,E3=−2.0 eV,E4=−1.125 eV
- (b) First excitation potential: 13.5 eV
- (c) Wavelengths emitted: 4950 Å,773 Å,917 Å
- (d) Photoelectric threshold wavelength: 915.74 Å
Topper's Solved these Questions
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.1
6 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Exercise 33.2
12 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Example Type 4
3 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MODERN PHYSICS - 2BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Level 2 Subjective
10 Videos
Similar Questions
The energy levels of a hypothetical one electron atom are shown in figure

Find the ionization potential of the atom.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
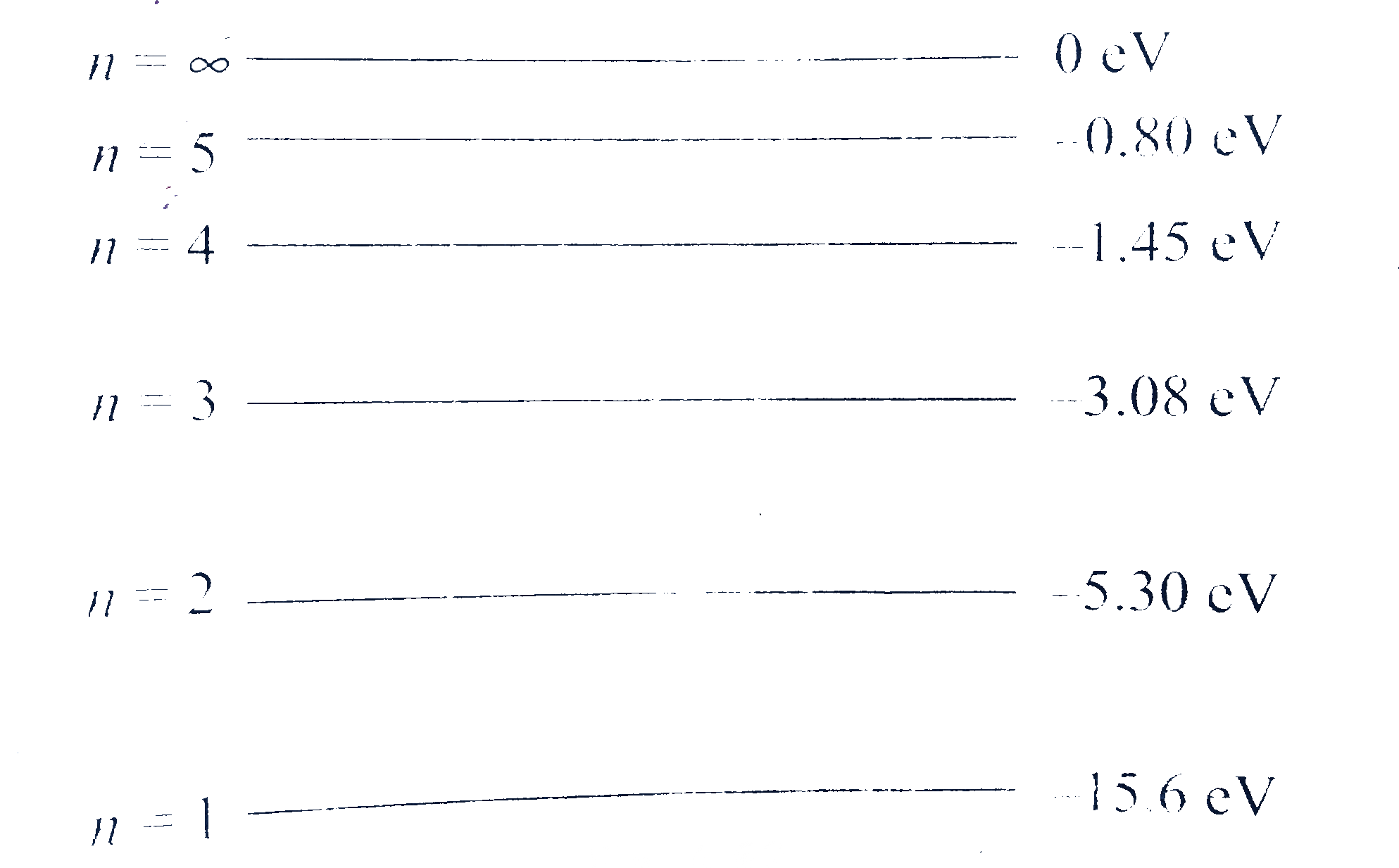
Find the excitation potential for the state n=3.
View SolutionIf an electron having kinetic energy 2eV is accelerated through the potential difference of 2 volt. Then calculate the wavelength associated with the electron
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure

Find the short wavelength limit of the series terminating at n=2.
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
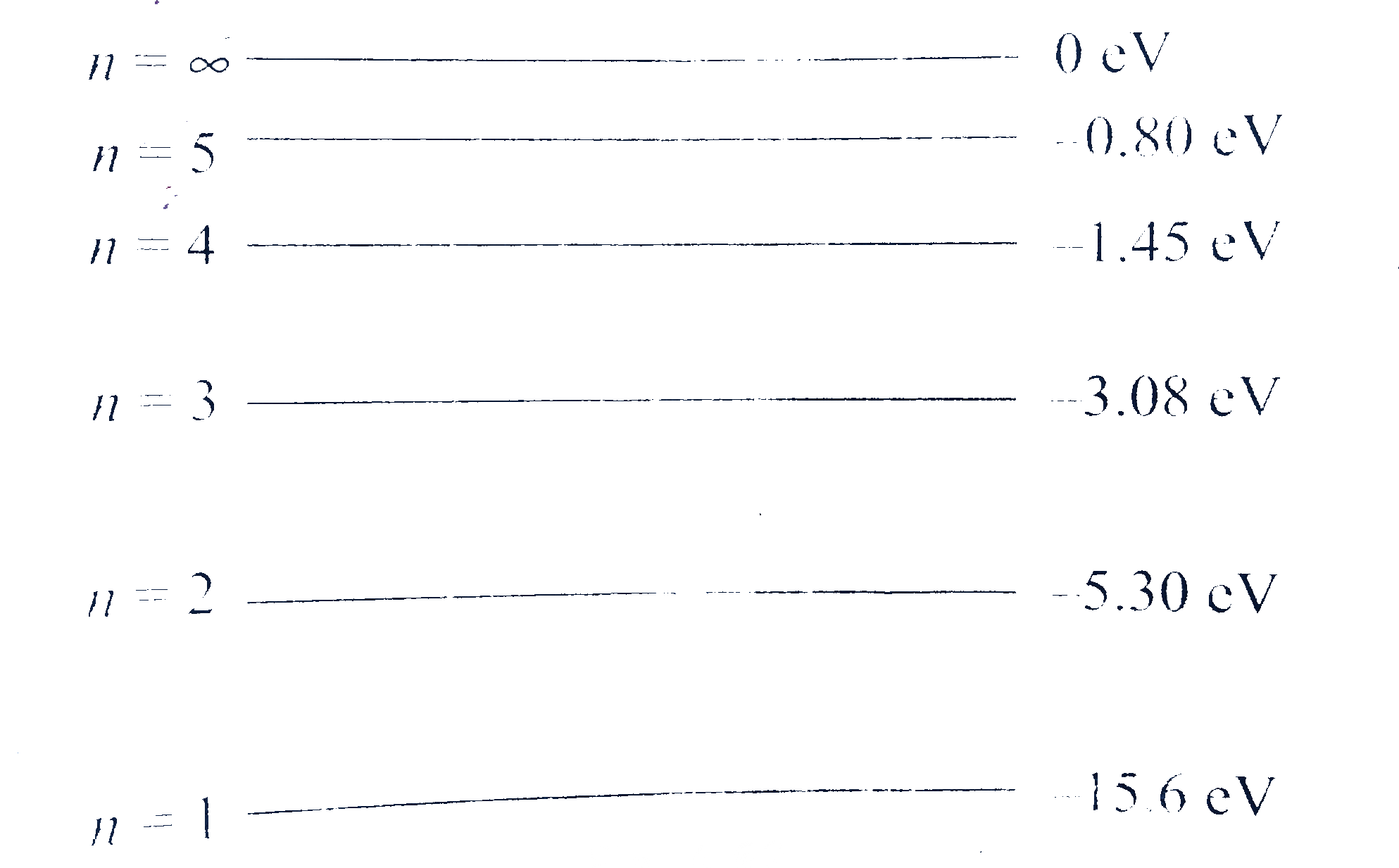
Find the wave number of the photon emitted for the transition n=3→n=1
View SolutionAn electron is excited to fourth energy level in an atom. It will
View SolutionIf the energy in the first excited state in hydrogen atom is 23.8eV then the potential energy of a hydrogen atom in the ground state can be assumed to be
View SolutionThe energy levels of a hypotherical one electron atom are shown in figure
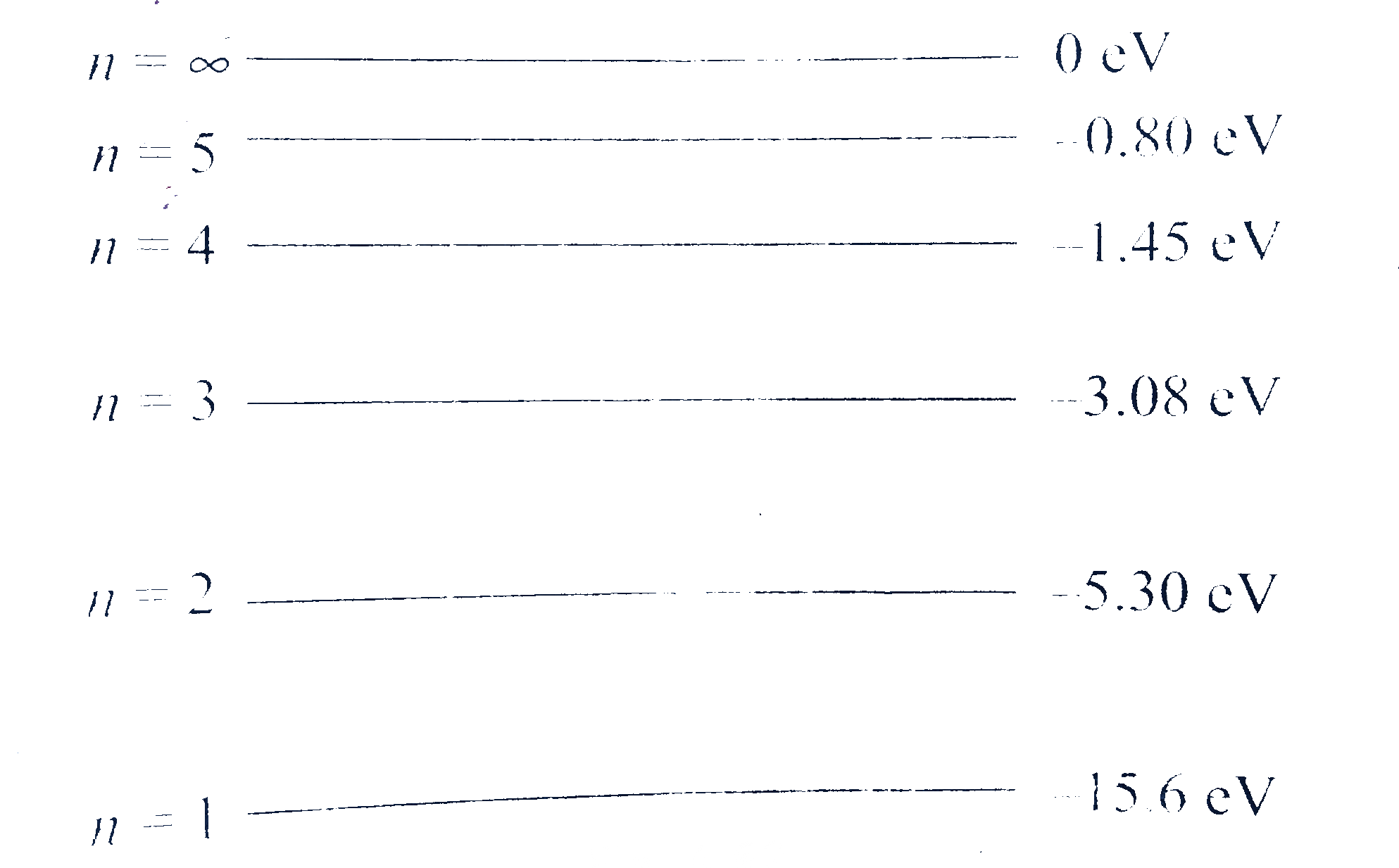
If an electron with initial kinetic energy 6eV is to interact with this hypothetical atom , what minimum energy will this electron carry after interaction?
View SolutionFigure shown the electron energy level , referred to the ground state (the lowest possible energy) as zero , for five different isoleted atoms. Which atom can produce radiation of the shortest wavelength when atoms in the ground state are bombarded with electrons energy W?

View SolutionA difference of 2.3 eV separates two energy levels in an atom. What is the frequency of radiation emitted when the atom transits form the upper level to the lower level.
View Solution
