The figure shows the variation of photocurrent with anode potential for a photosensitve surface for three different radiations. Let $l_{a}, l_{b} and l_{c}$ be the curves a, b and c, respectively
(a) $f_{a} = f_{b} and l_{a} \neq l_{b}$ (b) $f_{a} = f_{c} and l_{a} = l_{c}$
(c ) $f_{a} = f_{b} and l_{a} = l_{b}$ (d) $f_{b} = f_{c} and l_{b} = l_{c}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Saturation current is proportional to intensity while
stopping potential increases with increases in
frequency.
Hence, $f_{a} = f_{b} w h i \leq i_{a} < l_{b}$
Therefore, the correct option is (a).

|

Updated on:21/07/2023

Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The fig. shows the variation of photon current with anode potential for a photo-sensitive surface for three different radiation. Let $I_{a}, I_{b} and I_{c}$ be the intensities and $f_{a}, f_{b} and f_{c}$ be the frequency for the curves a,b and c respectively.

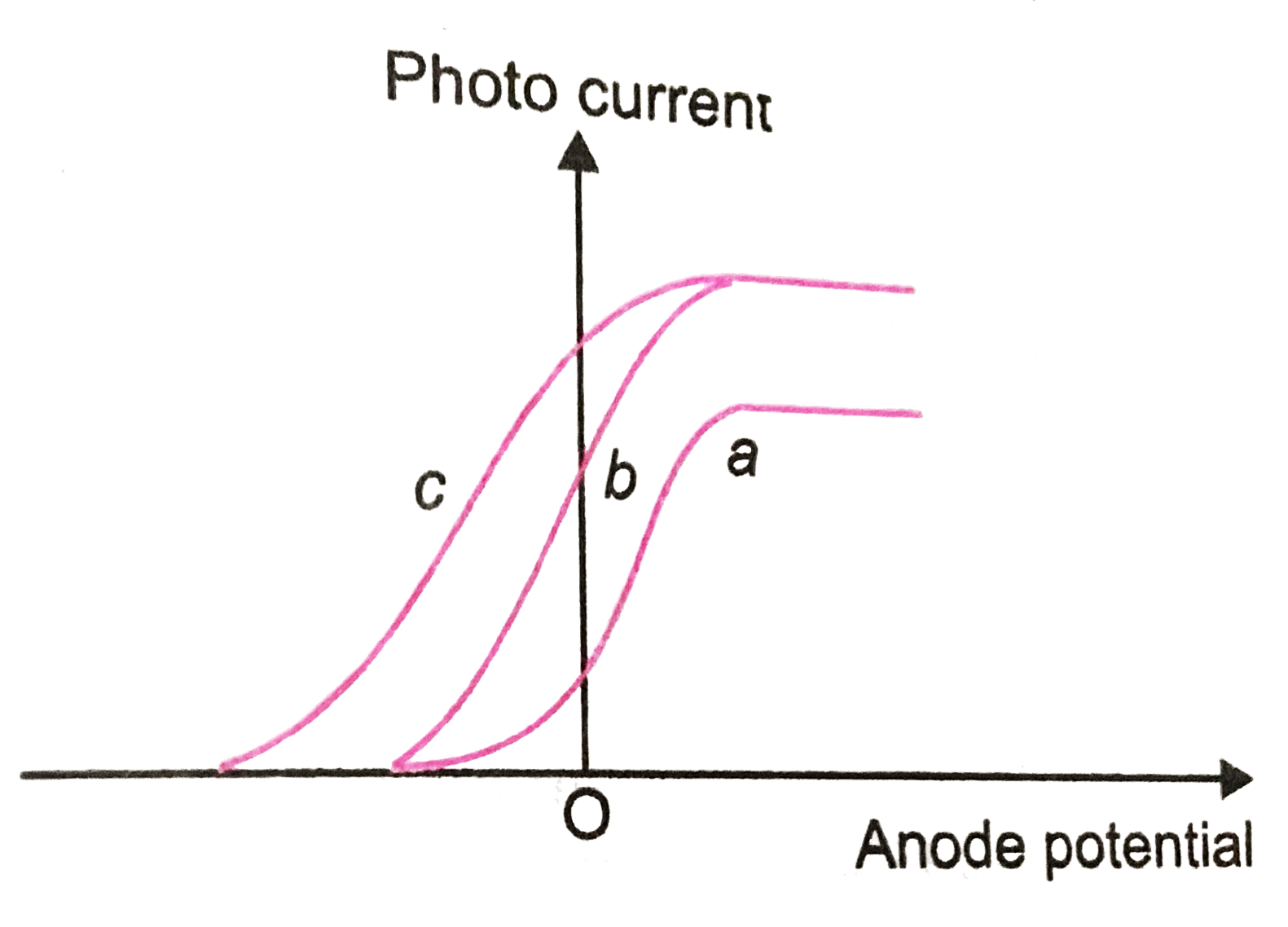A $v_{a} = v_{b} and I_{a} \neq I_{b}$
B $v_{a} = v_{c} and I_{a} = I_{c}$
C $v_{a} = v_{b} and I_{a} = I_{b}$
D $v_{b} = v_{c} and I_{b} = I_{c}$

DC PANDEY ENGLISH-MODERN PHYSICS - 1-Exercise 33.4

Home
Ask Doubt
Profile