A radioactive substance has a half-life of 64.8 h. A sample containing this isotope has an initial activity (t=0) of 40μCi. Calculate the number of nuclei that decay in the time interval between t1=10.0h and t2=12.0h.
The correct Answer is:A, C, D
To solve the problem of calculating the number of nuclei that decay between the time intervals t1=10.0h and t2=12.0h for a radioactive substance with a half-life of 64.8h and an initial activity of 40μCi, we can follow these steps:
Step 1: Calculate the Decay Constant (λ)
The decay constant λ can be calculated using the formula:
λ=ln(2)T1/2
where T1/2 is the half-life.
Given:
- T1/2=64.8h
Calculating λ:
λ=0.69364.8≈0.0107h−1
Step 2: Calculate the Initial Number of Nuclei (N0)
The initial activity A0 is related to the decay constant and the initial number of nuclei N0 by the formula:
A0=λN0
Rearranging gives:
N0=A0λ
Given:
- A0=40μCi=40×10−6Ci
- 1Ci=3.7×1010decays/s
Calculating A0 in decays per hour:
A0=40×10−6×3.7×1010decays/h≈1.48×106decays/h
Now substituting into the equation for N0:
N0=1.48×1060.0107≈1.38×108
Step 3: Calculate the Number of Nuclei at t1 and t2
Using the formula for radioactive decay:
N(t)=N0e−λt
At t1=10.0h:
N1=N0e−λt1=1.38×108e−0.0107×10≈1.24×108
At t2=12.0h:
N2=N0e−λt2=1.38×108e−0.0107×12≈1.214×108
Step 4: Calculate the Number of Decayed Nuclei
The number of nuclei that decay between t1 and t2 is given by:
ΔN=N1−N2
Calculating:
ΔN=1.24×108−1.214×108≈0.026×108≈2.6×106
Final Answer
The number of nuclei that decay between t1=10.0h and t2=12.0h is approximately 2.6×106.
---
- T1/2=64.8h
- A0=40μCi=40×10−6Ci
- 1Ci=3.7×1010decays/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Exercise 34.29videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Assertion And Reason11videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 2EXERCISE - Miscellaneous Examples9videos
MODERN PHYSICS - 2
- BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective23videos
MODERN PHYSICS - 1
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
Similar Questions
A radioactive substance has a half-life of h days. Find a formula for its mass m in terms of time t if the initial mass is m0. What is its initial decay rate?
View SolutionA radioactive isotope has a half-life of T years. The time required for its activity reduced to 6.25% of its original activity
View Solution
Knowledge Check
- Question 1 - Select One
A radioactive isotope X has a half life of 3 seconds. At t=0, a given sample of this isotope contains 8000 atom. Calculate (i) its decay constant (ii) average life (iii) the time t1, when 1000 atoms of the isotope X remain in the sample (iv) number of decay/sec in the sample at t=t1sec.
A2sB4sC7sD9s - Question 2 - Select One
The decay constant of a radioactive isotope is λ. If A1 and A2 are its activites at time t1 and t2 respectively, then the number of nuclei which have decayed the time (t1−t2)
AA1t1−A2t2BA1−A2C(A1−A2)/λDλ(A1−A2)
A radioactive substance has 108 nuclei. Its half life is 30 s . The number of nuclei left after 15 s is nearly
View SolutionHalf-life period of a radioactive substance is 6h. After 24h activity is 0.01μC, what was the initial activity ?
View SolutionHalf-life of a radioactive substance is T. At time t_1 activity of a radioactive substance is R1 and at time t2 it is R2. Find the number of nuclei decayed in this interval of time.
View SolutionA radioactive sample undergoes decay as per the following gragp. At timet=0, the number of undecayed nuclei is N0. Calculate the number of nuclei left after 1h.
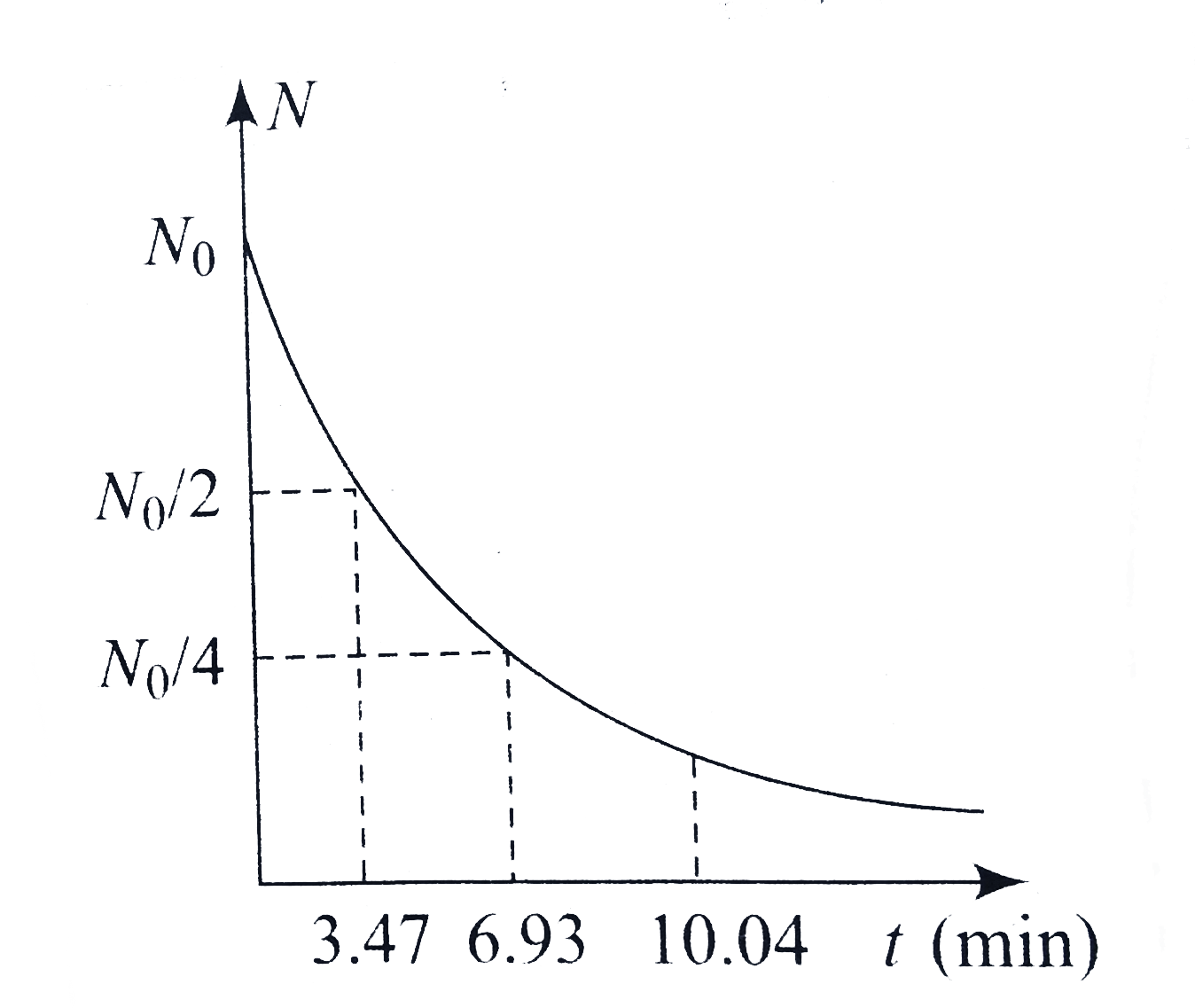 .View Solution
.View SolutionA radioactive sample undergoes decay as per the following gragp. At timet=0, the number of undecayed nuclei is N0. Calculate the number of nuclei left after 1h.
 .View Solution
.View SolutionTwo radioactive substances have half-lives T and 2T. Initially, they have equal number of nuclei. After time t=4T, the ratio of their number of nuclei is x and the ratio of their activity is y. Then,
View Solution

