One projectile moving with velocity v in space, gets burst into 2 parts of masses in the ratio 1:3. The smaller part becomes stationary. What is the velocity of thhe other part?
4v
v
4v3
3v4
The correct Answer is:C
To solve the problem step-by-step, we will use the principles of conservation of momentum.
1. Understanding the Problem:
- A projectile with an initial mass 4m is moving with a velocity v.
- It breaks into two parts with masses in the ratio 1:3.
- The smaller part (mass m) becomes stationary (velocity = 0).
- We need to find the velocity of the larger part (mass 3m).
2. Initial Momentum Calculation:
- The initial momentum Pi of the system can be calculated using the formula:
Pi=mass×velocity=4m⋅v
3. Final Momentum Calculation:
- After the explosion, the smaller part has a mass m and is stationary, so its momentum is:
Psmall=m⋅0=0
- The larger part has a mass 3m and we denote its velocity as V′. Thus, its momentum is:
Plarge=3m⋅V′
4. Applying Conservation of Momentum:
- According to the law of conservation of momentum, the total initial momentum must equal the total final momentum:
Pi=Psmall+Plarge
- Substituting the values we have:
4m⋅v=0+3m⋅V′
5. Solving for V′:
- Rearranging the equation gives:
4m⋅v=3m⋅V′
- Dividing both sides by 3m:
V′=4m⋅v3m
- The m cancels out:
V′=43v
6. Conclusion:
- The velocity of the larger part after the explosion is:
V′=43v
Final Answer:
The velocity of the other part (larger mass) is 43v.
---
- A projectile with an initial mass 4m is moving with a velocity v.
- It breaks into two parts with masses in the ratio 1:3.
- The smaller part (mass m) becomes stationary (velocity = 0).
- We need to find the velocity of the larger part (mass 3m).
- The initial momentum Pi of the system can be calculated using the formula:
Pi=mass×velocity=4m⋅v
- After the explosion, the smaller part has a mass m and is stationary, so its momentum is:
Psmall=m⋅0=0
- The larger part has a mass 3m and we denote its velocity as V′. Thus, its momentum is:
Plarge=3m⋅V′
- According to the law of conservation of momentum, the total initial momentum must equal the total final momentum:
Pi=Psmall+Plarge
- Substituting the values we have:
4m⋅v=0+3m⋅V′
- Rearranging the equation gives:
4m⋅v=3m⋅V′
- Dividing both sides by 3m:
V′=4m⋅v3m
- The m cancels out:
V′=43v
- The velocity of the larger part after the explosion is:
V′=43v
The velocity of the other part (larger mass) is 43v.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Taking it together73videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason21videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
- BOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
Similar Questions
A shell of mass m moving with velocity v suddenly breaks into 2 pieces. The part having mass m /4 remains stationary. The velocity of the other shell will be
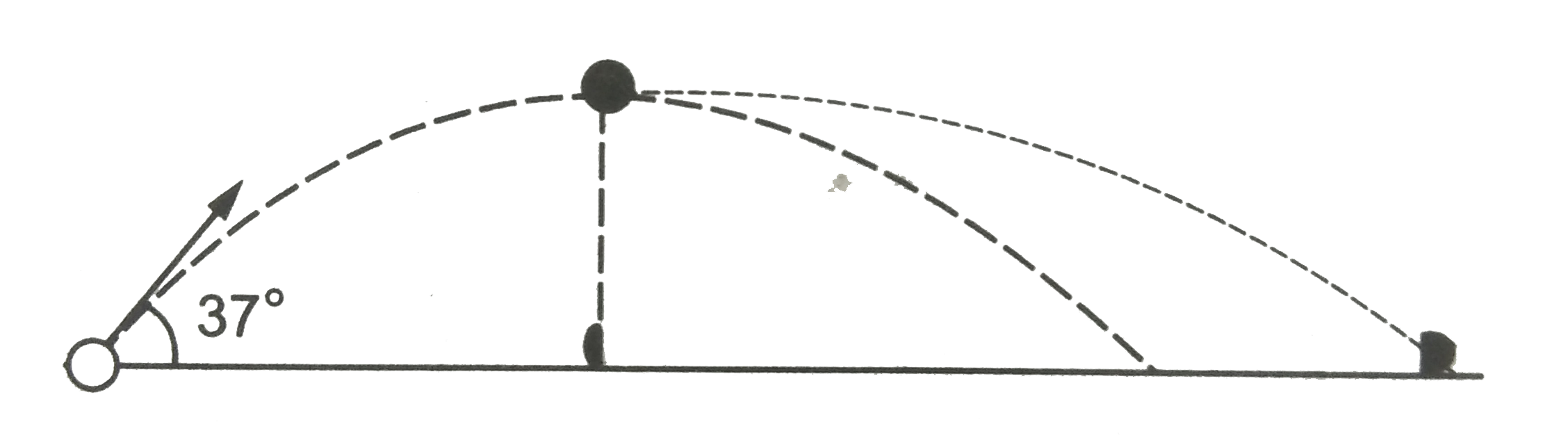
View SolutionA projectile is fired at a spedd of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Findthe distance from the launching point to the where the heavier piece lands.
 View Solution
View SolutionA shell of mass 10 kg is moving with a velocity with a velocity of 10ms−1 when it blasts and forms two parts of mass 9 kg and 1 kg respectively. If the 1st mass is stationary, the velocity of the 2nd is
View SolutionA projectile of mass 3kg is projected with velocity 50m/s at 37∘ from horizontal. After 2s, explosion takes place and the projectile breaks into two parts of masses 1kg and 2kg. The first part comes to rest just after explosion.
Find,
(a) the velocity of second part just after explosion.
(b) maximum height attained by this part. Take g=10m/s2View SolutionA projectile is fired at a speed of 100 m/s at an angel of 370 above the horizontal. At the highest point, the projectile breaks into two parts of mass ratio 1:3 the smaller coming to rest. Find the distance from the launching point to the where the heavier piece lands.
 View Solution
View SolutionA projectile moving vertically upwards with a velocity of 200 m/s breaks into two equal parts at the height of 490 m.one part starts moving vertically upwards with a velocity of 400 m/s.How much time after the break up wil the other part hit the ground?
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionA shell of mass m moving with a velocity breakes up suddenly into two pieces. The pa having mass m3 remains stationary. The velocity the other part will be
View SolutionA body of mass M moves in outer space with vleocity v. It is desired to break the body into two parts so that the mass of one part is one-tenth of the total mass. After the explosion, the heavier part comes to rest whole the lighter part continues to move in the original direction of motion. The velocity of the small part will be
View SolutionA mass of 1 kg is thrown up with a velocity of 100 m/s. After 5 seconds. It explodes into two parts. One parts of mass 400 g comes down with a velocity 25 m/s Calaculate the velocity of other parts:
View Solution

