F=2x2−3x−2. Choose correct option.
x=−1/2 is position of stable equilibrium
x = 2 is position of stable equilibrium
x=−1/2 is position of unstabl equilibrium
x = 2 is position of neutral equilibrium
The correct Answer is:A
To solve the problem given by the force equation F=2x2−3x−2 and to find the points of equilibrium, we will follow these steps:
Step 1: Set the Force Equation to Zero
To find the points of equilibrium, we need to set the force equation F to zero:
2x2−3x−2=0
Step 2: Factor the Quadratic Equation
Next, we will factor the quadratic equation. We can rearrange the equation:
2x2−4x+x−2=0
Now, we can group the terms:
(2x2−4x)+(x−2)=0
Factoring out common terms:
2x(x−2)+1(x−2)=0
Now, we can factor by grouping:
(2x+1)(x−2)=0
Step 3: Solve for x
Setting each factor to zero gives us the possible values of x:
1. 2x+1=0 leads to x=−12
2. x−2=0 leads to x=2
Step 4: Determine Stability of Equilibrium Points
To determine the stability of these equilibrium points, we need to find the derivative of the force function:
dFdx=4x−3
Now, we will evaluate the derivative at the equilibrium points:
1. For x=−12:
dFdx=4(−12)−3=−2−3=−5(negative, stable equilibrium)
2. For x=2:
dFdx=4(2)−3=8−3=5(positive, unstable equilibrium)
Conclusion
The points of equilibrium are x=−12 (stable) and x=2 (unstable). Therefore, the correct option for stable equilibrium is:
Option A: x=−12
To find the points of equilibrium, we need to set the force equation F to zero:
2x2−3x−2=0
Next, we will factor the quadratic equation. We can rearrange the equation:
2x2−4x+x−2=0
Now, we can group the terms:
(2x2−4x)+(x−2)=0
Factoring out common terms:
2x(x−2)+1(x−2)=0
Now, we can factor by grouping:
(2x+1)(x−2)=0
Setting each factor to zero gives us the possible values of x:
1. 2x+1=0 leads to x=−12
2. x−2=0 leads to x=2
To determine the stability of these equilibrium points, we need to find the derivative of the force function:
dFdx=4x−3
Now, we will evaluate the derivative at the equilibrium points:
1. For x=−12:
dFdx=4(−12)−3=−2−3=−5(negative, stable equilibrium)
2. For x=2:
dFdx=4(2)−3=8−3=5(positive, unstable equilibrium)
The points of equilibrium are x=−12 (stable) and x=2 (unstable). Therefore, the correct option for stable equilibrium is:
Option A: x=−12
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Knowledge Check
In sub - part (i) to (x) choose the correct option and in sub - part (xi) to (xy), answer the questions as intructed .
The derivative of 1+x+x2+x(3)+….+x50 at x=1:A1275B1725C1257D1255If (x)=ax−1ax+1 , choose the correct statement.
I. f(-x)=f(x)
II. F(-x)=-f(x)
III. F(2x)=2f(x)AOnly IBOnly IICOnly IIIDBoth II and III
If F=2x2−3x−2, then select the correct statement
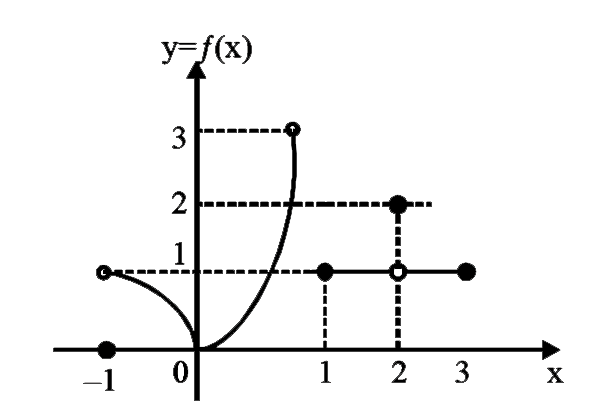
View SolutionIf f(x) is defined in −1≤x≤3 in the figure as shown then choose correct option
View SolutionIf f(x)=[√2sinx], where [x] represents the greatest integer function, then choose the incorrect option.
View SolutionIf f(x)=[√2sinx], where [x] represents the greatest integer function, then choose the incorrect option.
View Solution
Choose the correct option for X, Y and Z.
View SolutionLet f(x)=cosxsin2x then choose the best option :
View Solution
