The work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
240J
360 J
420 J
will depend upon the path
The correct Answer is:B
To find the work done by the force →F=−6x3^i N in displacing a particle from x=4m to x=−2m, we will use the concept of work done by a variable force. The work done, W, can be calculated using the integral of the force over the displacement.
1. Identify the Force Function:
The force is given as:
→F=−6x3^i
2. Set Up the Work Integral:
The work done by the force when moving from position x1 to x2 is given by:
W=∫x2x1Fxdx
Here, Fx=−6x3 and we need to integrate from x1=4m to x2=−2m.
3. Write the Integral:
W=∫−24−6x3dx
4. Factor Out the Constant:
Since −6 is a constant, we can factor it out of the integral:
W=−6∫−24x3dx
5. Calculate the Integral:
The integral of x3 is:
∫x3dx=x44
Therefore, we have:
W=−6(x44)−24
6. Evaluate the Definite Integral:
Now we evaluate the integral at the limits:
W=−6((−2)44−(4)44)
Calculate (−2)4=16 and (4)4=256:
W=−6(164−2564)
Simplifying:
W=−6(4−64)=−6(−60)=360J
Final Answer:
The work done by the force in displacing the particle from x=4m to x=−2m is:
360J
The force is given as:
→F=−6x3^i
The work done by the force when moving from position x1 to x2 is given by:
W=∫x2x1Fxdx
Here, Fx=−6x3 and we need to integrate from x1=4m to x2=−2m.
W=∫−24−6x3dx
Since −6 is a constant, we can factor it out of the integral:
W=−6∫−24x3dx
The integral of x3 is:
∫x3dx=x44
Therefore, we have:
W=−6(x44)−24
Now we evaluate the integral at the limits:
W=−6((−2)44−(4)44)
Calculate (−2)4=16 and (4)4=256:
W=−6(164−2564)
Simplifying:
W=−6(4−64)=−6(−60)=360J
The work done by the force in displacing the particle from x=4m to x=−2m is:
360J
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
The work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionThe work done by the force →F=6ˆi+2ˆj N in displacing an object from→r1=3ˆi+8ˆj to →r2=5ˆi−4ˆj m , is
View SolutionA force (F) acting on a particle varies work done by a particle varies with the with the position x as shown in figure
 .
.
Find the work done by by force in displacing the particle from .
(a) x=−2m to x=0
(b) x=0 to x=2m..
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA particle of mass 2kg travels along a straight line with velocity v=a√x, where a is a constant. The work done by net force during the displacement of particle from x=0 to x=4m is
View SolutionThe relationship between the force F and position x of body is as shown in figure. The work done in displacing the body in displacing the body from (x=1m to x=5m) will be
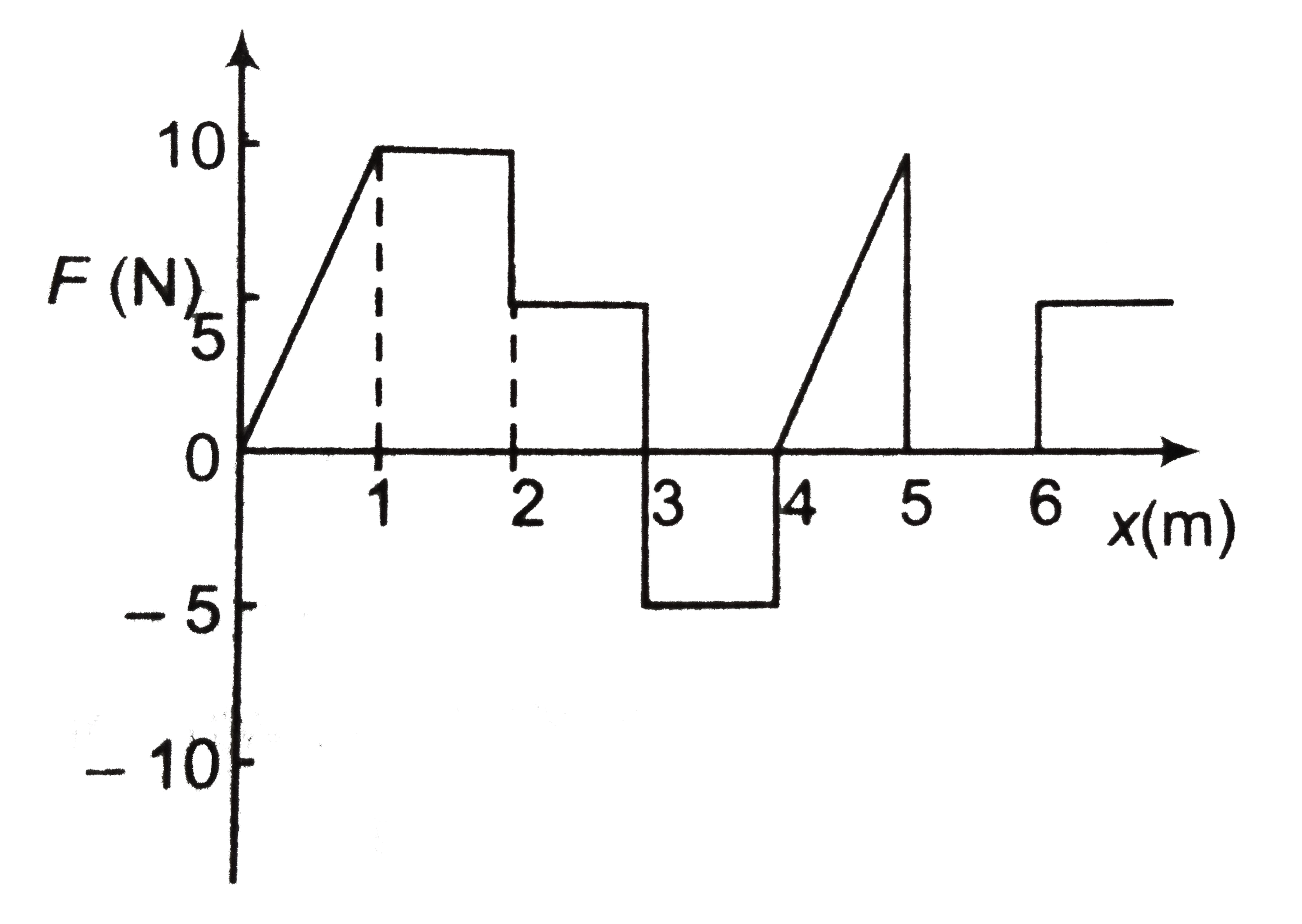 .
.
View SolutionFind the work done by the force F=3ˆi−ˆj−2ˆk acrting on a particle such that the particle is displaced from point A(−3,−4,1)⊤o∈tB(−1,−1,−2).
View SolutionFind the work done by the force F=3ˆi−ˆj−2ˆk acrting on a particle such that the particle is displaced from point A(−3,−4,1)→B(−1,−1,−2).
View SolutionFind the work done by the force F=3ˆi−ˆj−2ˆk acting on a particle such that the particle is displaced from point A(−3,−4,1)topointB(−1,−1,−2).
View Solution
