A particle is moved from (0, 0) to (a, a) under a force a F=(3ˆi+4ˆj) from two paths. Path 1 is OP and path 2 is OPQ. Let W1 and W2 be the work done by this force in these two paths. Then,
W1=W2
W1=2W2
W2=2W1
W2=4W1
The correct Answer is:A
To solve the problem, we need to calculate the work done by the force F=3^i+4^j along two different paths from the point O(0,0) to the point A(a,a).
Step 1: Define the paths.
- Path 1 (OP): Directly from O(0,0) to A(a,a).
- Path 2 (OPQ): From O(0,0) to P(a,0), then to Q(a,a).
Step 2: Calculate the work done along Path 1 (OP).
- The displacement vector for Path 1 is:
d1=A−O=(a,a)−(0,0)=a^i+a^j
- The work done W1 is given by the dot product of the force and the displacement:
W1=F⋅d1=(3^i+4^j)⋅(a^i+a^j)
- Calculating the dot product:
W1=3a+4a=7a
Step 3: Calculate the work done along Path 2 (OPQ).
- For Path 2, we break it into two segments: OP and PQ.
1. Work done along OP:
- Displacement vector for OP is the same as before:
dOP=a^i+0^j
- Work done WOP:
WOP=F⋅dOP=(3^i+4^j)⋅(a^i+0^j)=3a
2. Work done along PQ:
- Displacement vector for PQ is:
dPQ=(a,a)−(a,0)=0^i+a^j
- Work done WPQ:
WPQ=F⋅dPQ=(3^i+4^j)⋅(0^i+a^j)=4a
- Total work done along Path 2 W2:
W2=WOP+WPQ=3a+4a=7a
Step 4: Compare the work done along both paths.
- We found that:
W1=7aandW2=7a
- Therefore, we conclude that:
W1=W2
Final Answer:
The work done along both paths is equal:
W1=W2
- Path 1 (OP): Directly from O(0,0) to A(a,a).
- Path 2 (OPQ): From O(0,0) to P(a,0), then to Q(a,a).
- The displacement vector for Path 1 is:
d1=A−O=(a,a)−(0,0)=a^i+a^j
- The work done W1 is given by the dot product of the force and the displacement:
W1=F⋅d1=(3^i+4^j)⋅(a^i+a^j)
- Calculating the dot product:
W1=3a+4a=7a
- For Path 2, we break it into two segments: OP and PQ.
- Displacement vector for OP is the same as before:
dOP=a^i+0^j
- Work done WOP:
WOP=F⋅dOP=(3^i+4^j)⋅(a^i+0^j)=3a
- Displacement vector for PQ is:
dPQ=(a,a)−(a,0)=0^i+a^j
- Work done WPQ:
WPQ=F⋅dPQ=(3^i+4^j)⋅(0^i+a^j)=4a
W2=WOP+WPQ=3a+4a=7a
- We found that:
W1=7aandW2=7a
- Therefore, we conclude that:
W1=W2
The work done along both paths is equal:
W1=W2
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A particle is moved from (0,0)→(a,a) under a force F=(x2ˆi+y3ˆj) from two paths. Path 1 si OP and Path 2 is OQP. Let W1 and W2 be the work done by this force in these two paths. Then

View SolutionA given mass of a gas expands from the state A to the state B by three paths 1,2 and 3 as shown in the figure, If W1,W2 and W3 respectively be the work done by the gas along the three paths then

View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
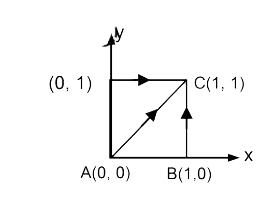
View SolutionA given mass of gas expands from state A to state B by three paths 1, 2, and 3 as shown in the figure :
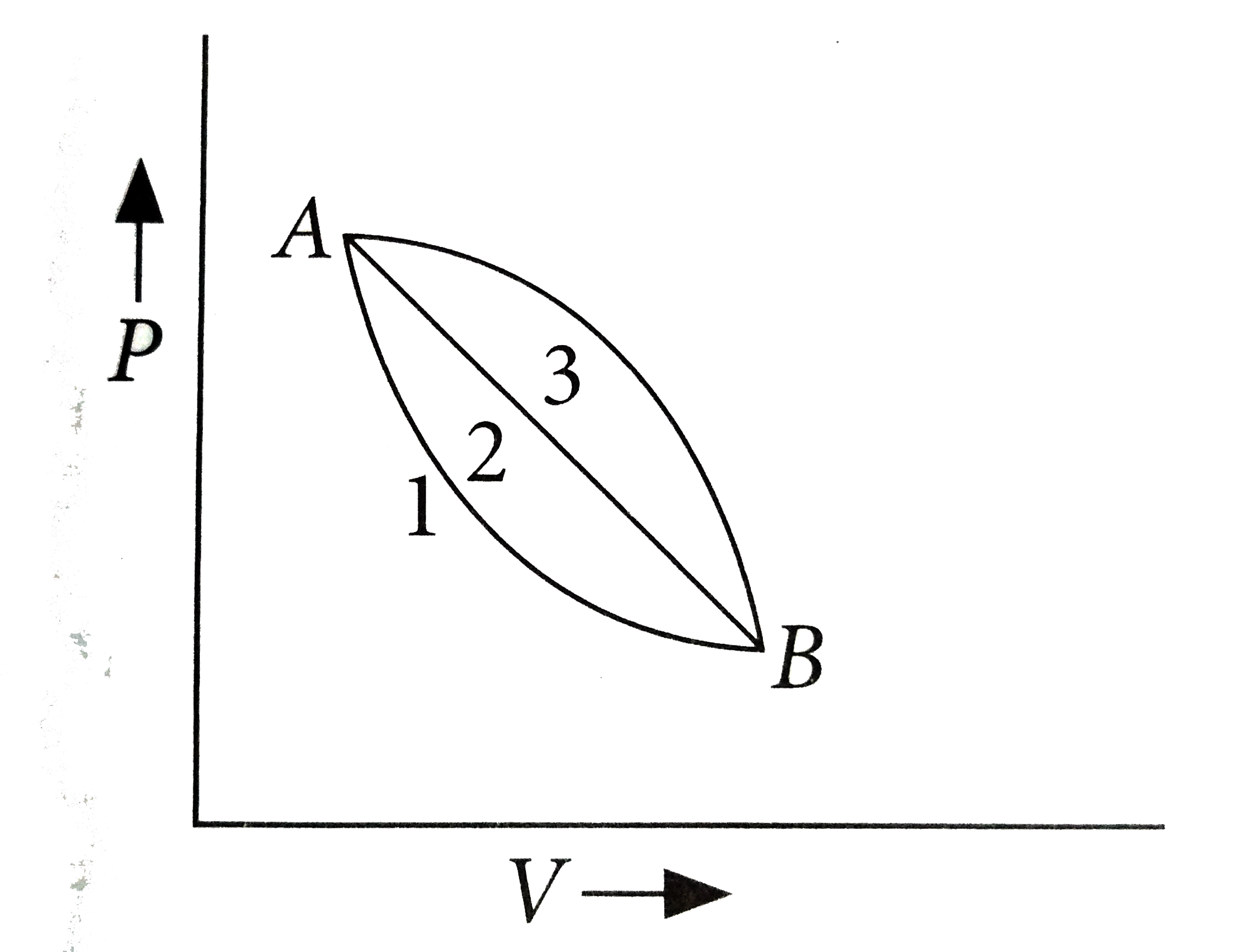
If w1,w2andw3 respectively, be the work done by the gas along three paths, then
View SolutionAn object is moving along a straight line path from P to Q under the action of a force →F=(4ˆi−3ˆj+ˆ2k)N. If the co-ordinate of P and Q in meters are (3,2,-1) and (2,-1,4) respectively. Then the work done by the force is
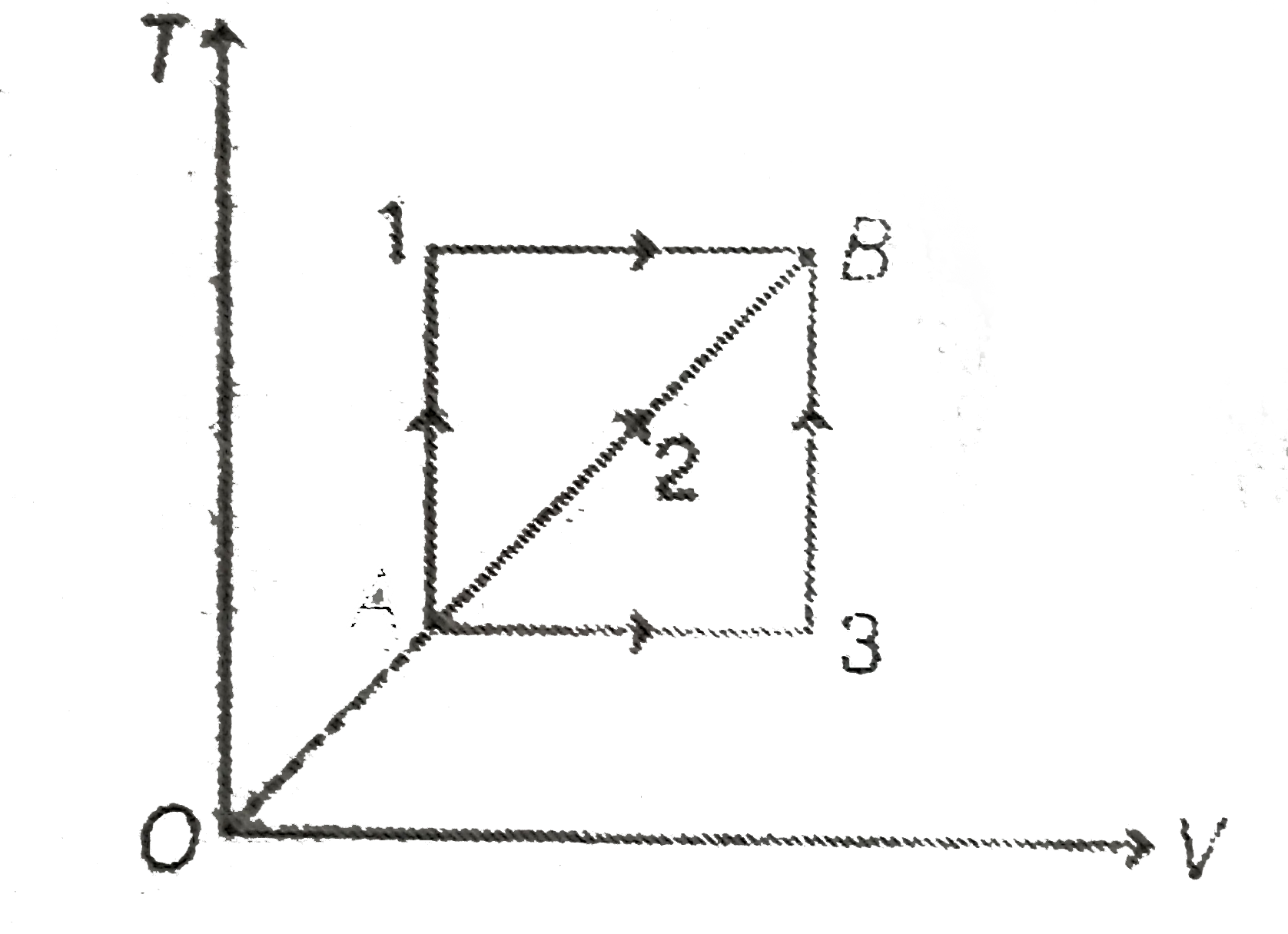
View SolutionA givne mass of a gas expands from a state A to the state B by three paths 1, 2 and 3 as shown in T-V indicator diagram. If W1,W2 and W3 respectively be the work done by the gas along the three paths, then
View SolutionA given mass of gas expands from state A to state b by three paths 1,2, and 3 as shown in the figure below. If w1,w2 and w3, respectively, be the work done by the gas along three paths, then
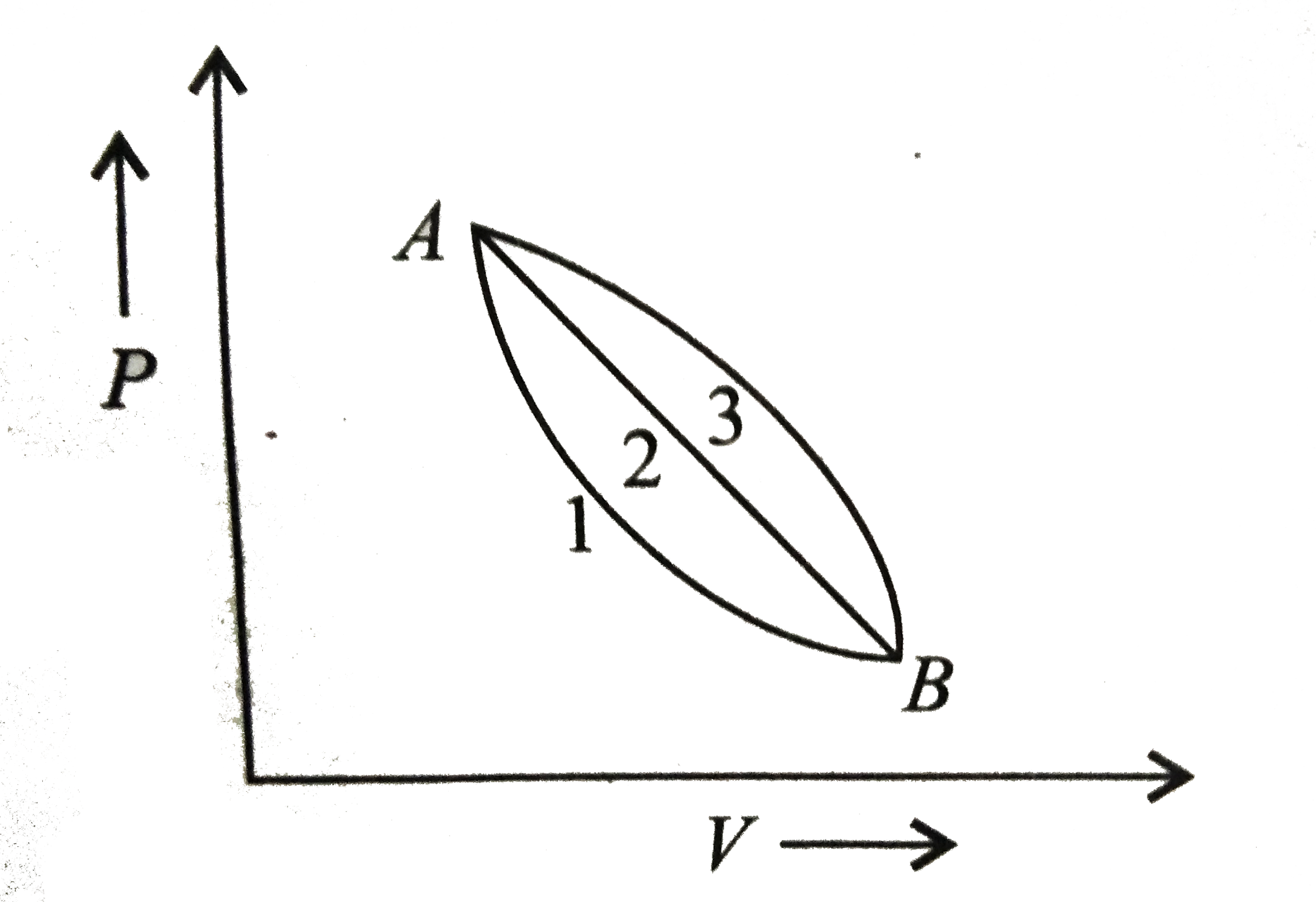
View SolutionA given mass of gas expands from state A to state B by three paths 1,2, and 3 as shown in the figure below. If w1,w2 and w3, respectively, be the work done by the gas along three paths, then

View SolutionA particle is acted upon by only a conservative force F=(7ˆi−6ˆj) N (no other force is acting on the particle). Under the influence of this force particle moves from (0, 0) to (-3m, 4m) then
View SolutionA particle moves from position 3ˆi+2ˆj−6ˆk to 14ˆi+13ˆj+9ˆk due to a uniform force of 4ˆi+ˆj+3ˆkN. If the displacement is in meters, then find the work done by the force.
View Solution
