A spring and block are placed on a fixed smooth wedge as shown. Following conclusions can be drawn for the block.
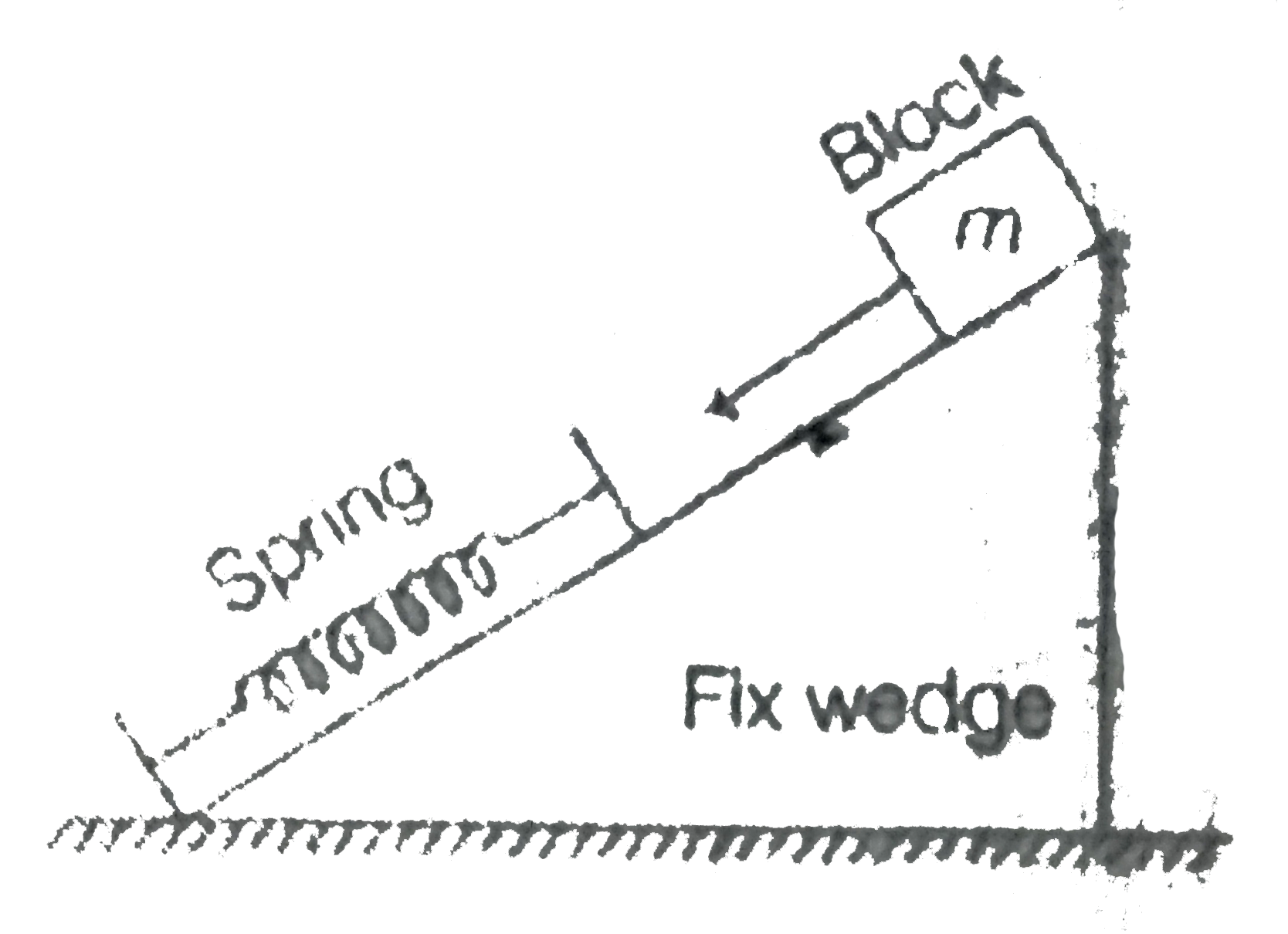
(i) magnitude of its momentum will be maximum when Fnet on block is zero
(ii) its kinetic energy will be maximum when Fnet on block is zero
(iii) kinetic energy of block is maximum when block just touches the spring
(iv) net force on block is maximum when KE = 0
(i), (iii), (iv)
(ii), (iii), (iv)
(i), (ii), (iii)
(i), (ii), (iv)
The correct Answer is:D
Step by step video & image solution for A spring and block are placed on a fixed smooth wedge as shown. Following conclusions can be drawn for the block. (i) magnitude of its momentum will be maximum when F_("net") on block is zero (ii) its kinetic energy will be maximum when F_("net") on block is zero (iii) kinetic energy of block is maximum when block just touches the spring (iv) net force on block is maximum when KE = 0 by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
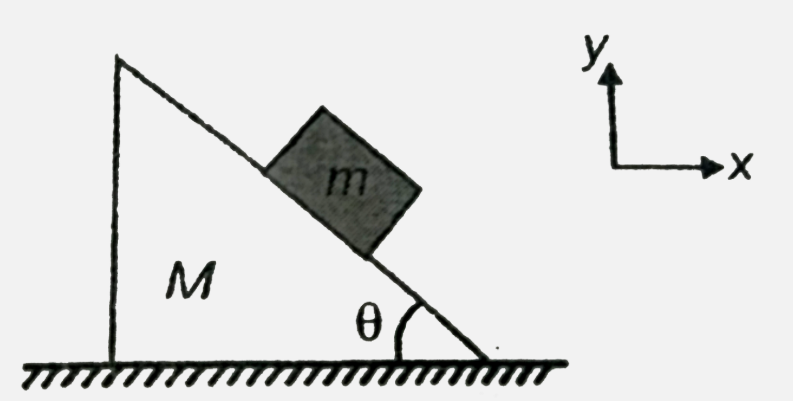
A block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionIn a horizontal spring-block system force constant of spring is k = 16N/m, mass of the block is 1 kg. Maximum kinetic energy of the block is 8J. Then
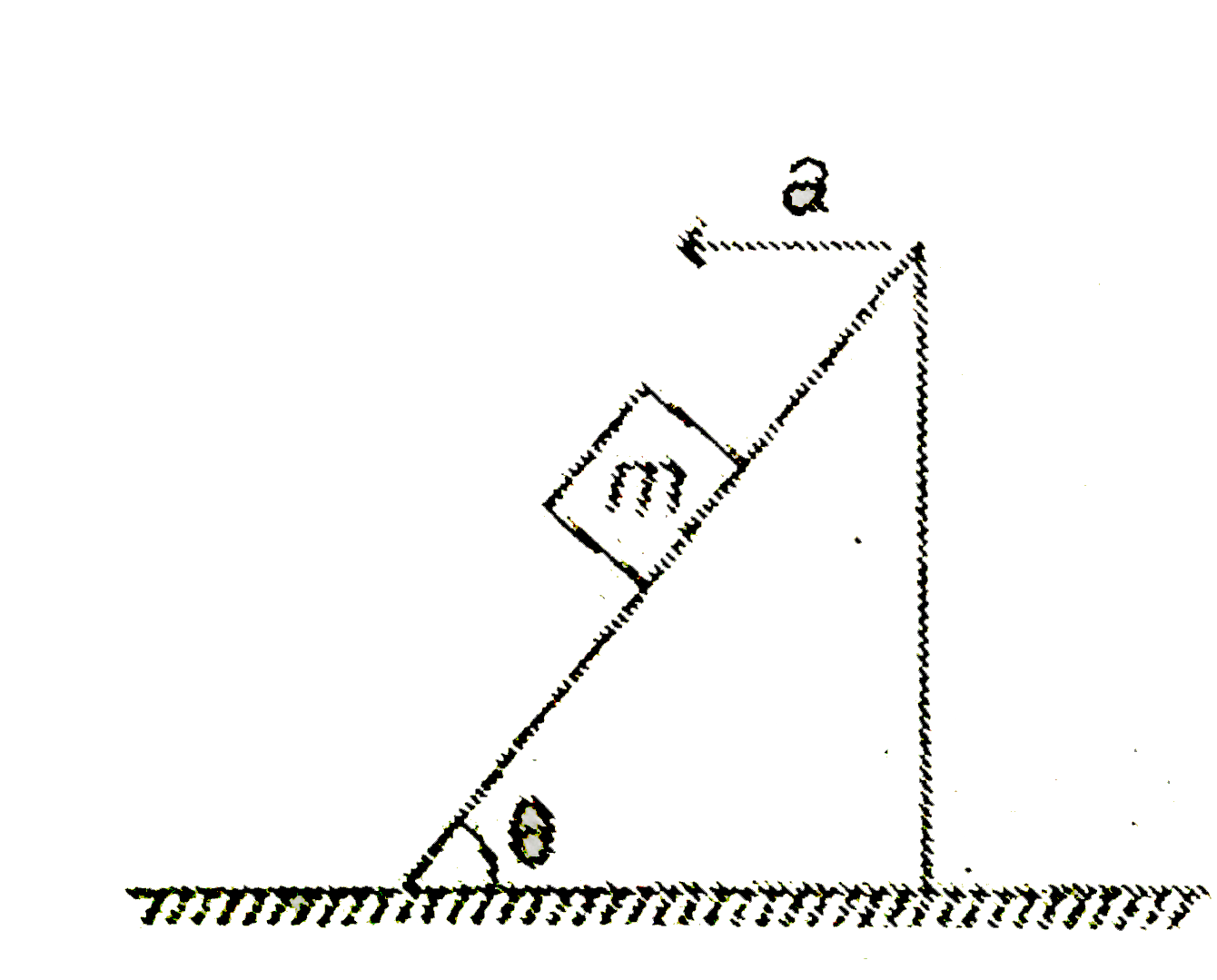
View SolutionAs shown in the figure a block of mass 'm' is placed on a smooth wedge moving with constant acceleration such that block does not move with respect to the wedge. Find work done by the net force on the block in time t. (Initial speed is 0)
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.

Maximum compression of the spring in the collision will be nearly
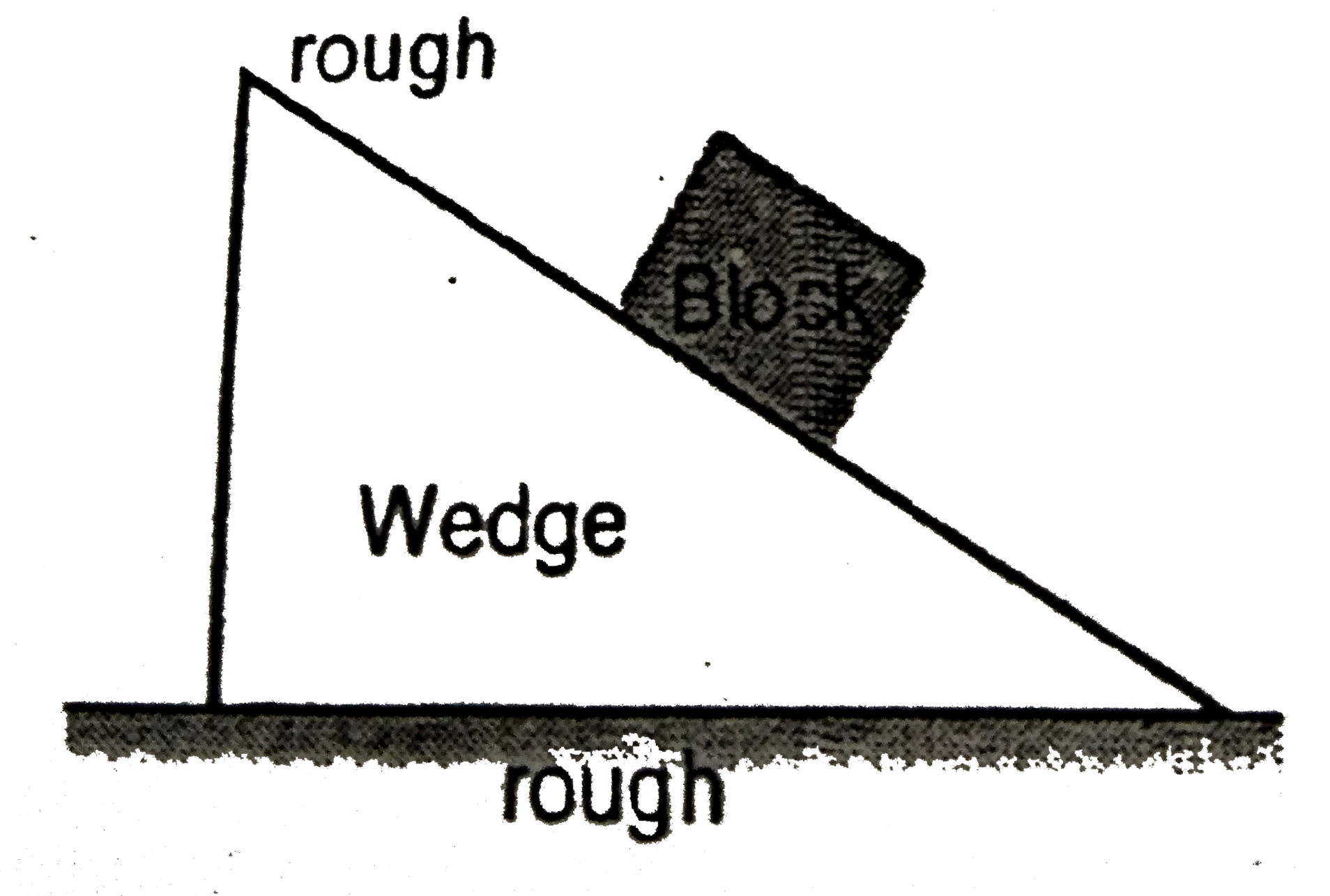
View SolutionWhen a block is placed on a wedge as shown in figure, the block starts sliding down and the wedge also start sliding on ground. All surfaces are rough. The centre of mass of ( wedge + block ) system will move.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View SolutionThe spring shown in figure is unstretched when a man starts pulling on the cord. The mass of the block is M. If the man exerts a constant force F, find

(a) the amplitude and the time period of the motion of the block,
(b) the energy stored in the spring when the block passes through the equilibrium position and
(c) the kinetic energy of the block at this position.
View Solution
