An automobile enters a turn whose radius is R. The road is banked at angle θ. Fricton is negligible between wheels of the automobile and road, Mass of automobile is m and speed is v. Select the correct alternative.
net force on the automobile is zero
normal reaction on the automobile is mgcosθ
normal reaction on the automobile is mgsecθ
net force on the automobile is √(mg)2+(mv2/R)2
The correct Answer is:C
To solve the problem of an automobile entering a banked turn with negligible friction, we can analyze the forces acting on the automobile and apply the concepts of circular motion. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Forces Acting on the Automobile
When the automobile is on a banked road, the following forces act on it:
- The weight of the automobile (mg) acting downward.
- The normal force (N) acting perpendicular to the surface of the road.
Step 2: Resolve the Normal Force into Components
Since the road is banked at an angle θ, we can resolve the normal force into two components:
- The vertical component: Ncosθ
- The horizontal component: Nsinθ
Step 3: Set Up the Equations for Forces
1. In the vertical direction, the forces must balance since there is no vertical acceleration:
Ncosθ=mg
From this, we can express the normal force:
N=mgcosθ
2. In the horizontal direction, the horizontal component of the normal force provides the necessary centripetal force for circular motion:
Nsinθ=mv2R
Step 4: Substitute the Expression for Normal Force
Substituting N=mgcosθ into the horizontal force equation:
mgcosθsinθ=mv2R
Step 5: Simplify the Equation
Canceling m from both sides (assuming m≠0):
gsinθcosθ=v2R
This can be rewritten using the definition of tangent:
gtanθ=v2R
Step 6: Conclusion
From the derived equation, we can analyze the relationship between the speed v, the radius R, and the angle θ. The correct expression derived from the forces indicates that the normal force is not simply mg or mgcosθ, but rather N=mgcosθ.
Final Answer
Thus, the correct alternative is:
- Option C: The normal reaction on the automobile is mgsecθ.
When the automobile is on a banked road, the following forces act on it:
- The weight of the automobile (mg) acting downward.
- The normal force (N) acting perpendicular to the surface of the road.
Since the road is banked at an angle θ, we can resolve the normal force into two components:
- The vertical component: Ncosθ
- The horizontal component: Nsinθ
1. In the vertical direction, the forces must balance since there is no vertical acceleration:
Ncosθ=mg
From this, we can express the normal force:
N=mgcosθ
Nsinθ=mv2R
Substituting N=mgcosθ into the horizontal force equation:
mgcosθsinθ=mv2R
Canceling m from both sides (assuming m≠0):
gsinθcosθ=v2R
This can be rewritten using the definition of tangent:
gtanθ=v2R
From the derived equation, we can analyze the relationship between the speed v, the radius R, and the angle θ. The correct expression derived from the forces indicates that the normal force is not simply mg or mgcosθ, but rather N=mgcosθ.
Thus, the correct alternative is:
- Option C: The normal reaction on the automobile is mgsecθ.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Comprehension
13 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - JEE Main
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A car is negotiating a curved road of radius R. The road is banked at angle θ. The coefficeint of friction between the tyres of the car and the road is μs. The maximum safe velocity on this road is
View SolutionAn automobile enters a turn of radius R. If the road is banked at an angle of 45∘ and the coefficient of friction is 1, the minimum and maximum speed with which the automobile can negotiate the turn without skidding is :
View Solution
Knowledge Check
A circular racetrack of radius 300 m is banked at an angle of 15∘ If the coefficient of friction between the wheels of a race car and the road is 0.2 what is the (a) optimum speed of the race car to avoid wear and tear on its tyres , and (b) maximum permissible speed to aviod slipping ?
A10√3ms−1B9√10ms−1C√10ms−1D2√10ms−1
A circular racetrack of radius 300 m is banked at an angle of 15∘ If the coefficient of friction between the wheels of a race car and the road is 0.2 what is the (a) optimum speed of the race car to avoid wear and tear on its tyres , and (b) maximum permissible speed to aviod slipping ?
View SolutionA circular racetrack of radius 300 m is banked at an angle of 15∘ The coefficient of friction between the wheels of a race car and the road is 0.2. The optimum speed of the race car to avoid wear and tear on its tyres is
View SolutionA wedge of inclination θ is placed on a smooth surface. Ablock of mass m placed on the wedge is found to be stationary w.r.t the wedge . Select the correct alternative .
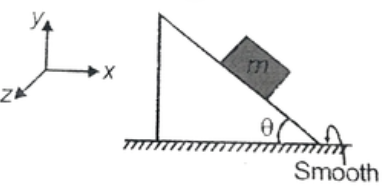
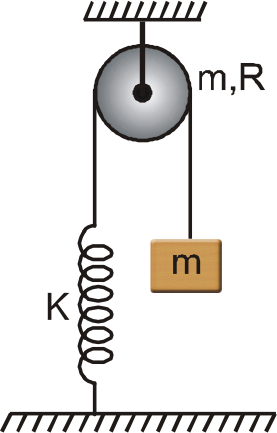
View SolutionA uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is 3mgK, where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).
View SolutionA cyclist moves along a curved road with a velocity v. The road is banked for speed v. The angle of banking is θ.Which of the following statements in not true?
View SolutionA car is moving on a circular road which is rough and banked at angle . If radius of circular track is R then. Choose correct statement:
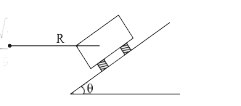
View SolutionA car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View Solution
