Question

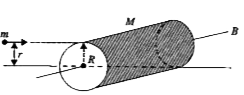
A particle of mass m and velocity $v_0$ is fired at a solid cylinder of mass M and radius R. The cylinder is initially at rest and is mounted on a fixed horizontal axle that runs through the centre of mass. The line of motion of the particle is perpendicular to the axle and at a distance d, less than R, from the centre and the particle sticks to the surface of the cylinder, then

Options

A. Angular speed of the system just after the particle stick is `(2 mv_(0)d)/(R^(2)(M+2m))`
B. Mechanical energy is conserved
C. angular speed of the system just after the particle sticks is `( mv_(0)d)/(R^(2)(M+2m))`
D. Mechanical energy is not conserved

Answer

A::D

Explanation

To solve the problem step by step, we will apply the principles of conservation of angular momentum and analyze the system before and after the collision.

Step 1: Understand the system
We have a solid cylinder of mass \( M \) and radius \( R \) that is initially at rest. A particle of mass \( m \) is fired with an initial velocity \( v_0 \) at a distance \( d \) from the center of the cylinder, perpendicular to the axle. When the particle collides with the cylinder, it sticks to it.

Step 2: Calculate the initial angular momentum
Before the collision, the angular momentum \( L_i \) of the particle about the center of the cylinder can be calculated as:
\( L_i = m v_0 d \)
where \( d \) is the perpendicular distance from the line of motion of the particle to the axis of rotation (the center of the cylinder).

Step 3: Calculate the moment of inertia of the system after the collision
After the particle sticks to the cylinder, we need to find the moment of inertia \( I \) of the combined system (cylinder + particle).

- The moment of inertia of the solid cylinder about its center is:
\( I_{\text{cylinder}} = \frac{1}{2} M R^2 \)

- The moment of inertia of the particle (considered as a point mass) at a distance \( R \) from the center is:
\( I_{\text{particle}} = m R^2 \)

Thus, the total moment of inertia \( I \) of the system after the collision is:
\( I = I_{\text{cylinder}} + I_{\text{particle}} = \frac{1}{2} M R^2 + m R^2 \)

Step 4: Apply conservation of angular momentum
According to the conservation of angular momentum:
\( L_i = L_f \)
where \( L_f \) is the final angular momentum of the system after the collision. The final angular momentum can be expressed as:
\( L_f = I \omega \)
where \( \omega \) is the angular velocity of the system after the collision.

Setting the initial and final angular momentum equal gives:
\( m v_0 d = \left( \frac{1}{2} M R^2 + m R^2 \right) \omega \)

Step 5: Solve for angular velocity \( \omega \)
Rearranging the equation to solve for \( \omega \):
\( \omega = \frac{m v_0 d}{\frac{1}{2} M R^2 + m R^2} \)
This can be simplified further:
\( \omega = \frac{2 m v_0 d}{M R^2 + 2 m R^2} \)

Step 6: Determine if mechanical energy is conserved
In this case, mechanical energy is not conserved because the collision is inelastic (the particle sticks to the cylinder). Therefore, some kinetic energy is transformed into other forms of energy (like heat) during the collision.

Final Answer
The angular speed of the system just after the particle sticks is:
\( \omega = \frac{2 m v_0 d}{M R^2 + 2 m R^2} \)
Mechanical energy is not conserved.