A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
F2m
3F4m
F4m
3F2m
The correct Answer is:C
Step by step video & image solution for A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc. Acceleration of the plank is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
16 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.When a horizontal force F is applied at centre of sphere, acceleration of the plank is

View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
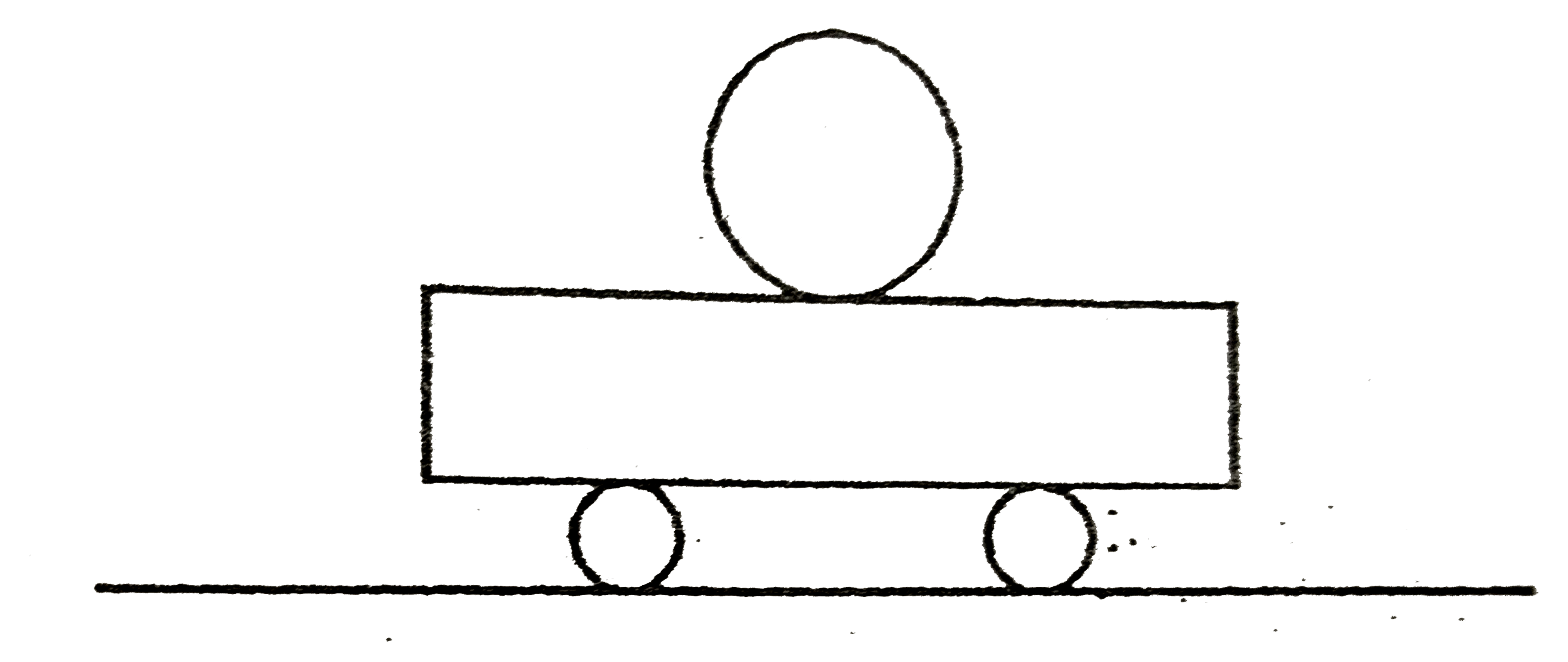
Angular acceleration of sphere is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
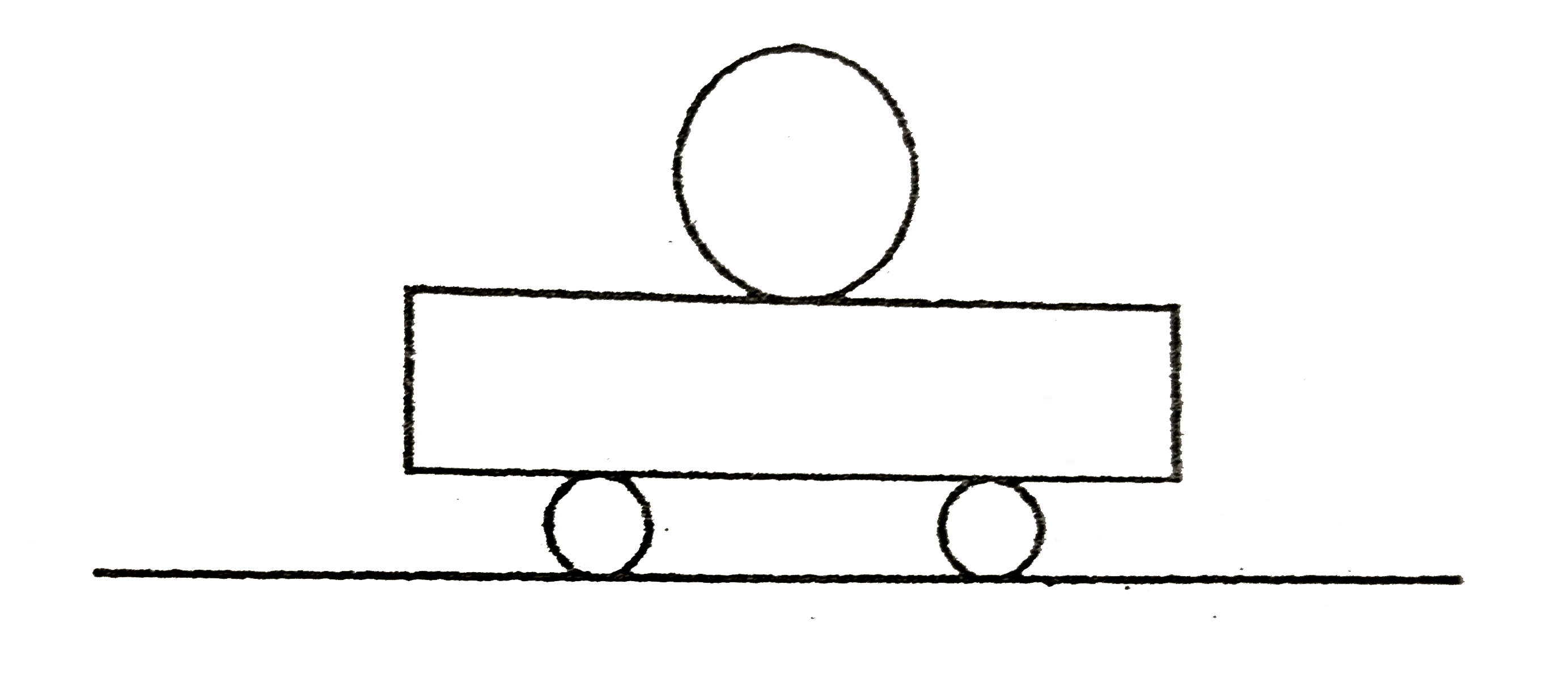
Acceleration of centre of mass of sphere is
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

A Horizontal force F is applied on the plank. What is the maximum value of F, if μ is coefficient of friction between sphere movment and plank and there is no slipping ?
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping. Force of friction between sphere and plank is

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

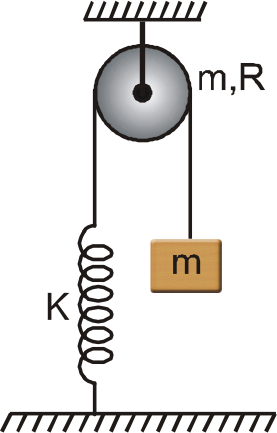
View SolutionA uniform disc of mass m and radius R is free to rotate about its fixed horizontal axis without friction. There is sufficient friction between the inextensible light string and disc to prevent slipping of string over disc. At the shown instant extension in light spring is 3mgK, where m is mass of block, g is acceleration due to gravity and K is spring constant. Then select the correct alternative(s).
View SolutionChoose the correct option:
A sphere of mass m is given some angular velocity about a horizontal axis through its centre and gently placed on a plank of mass 'm'. The co-efficient of friction between the two is μ. The plank rests on a smooth horizontal surface. The initial acceleration of the centre of sphere relative to the plank will be
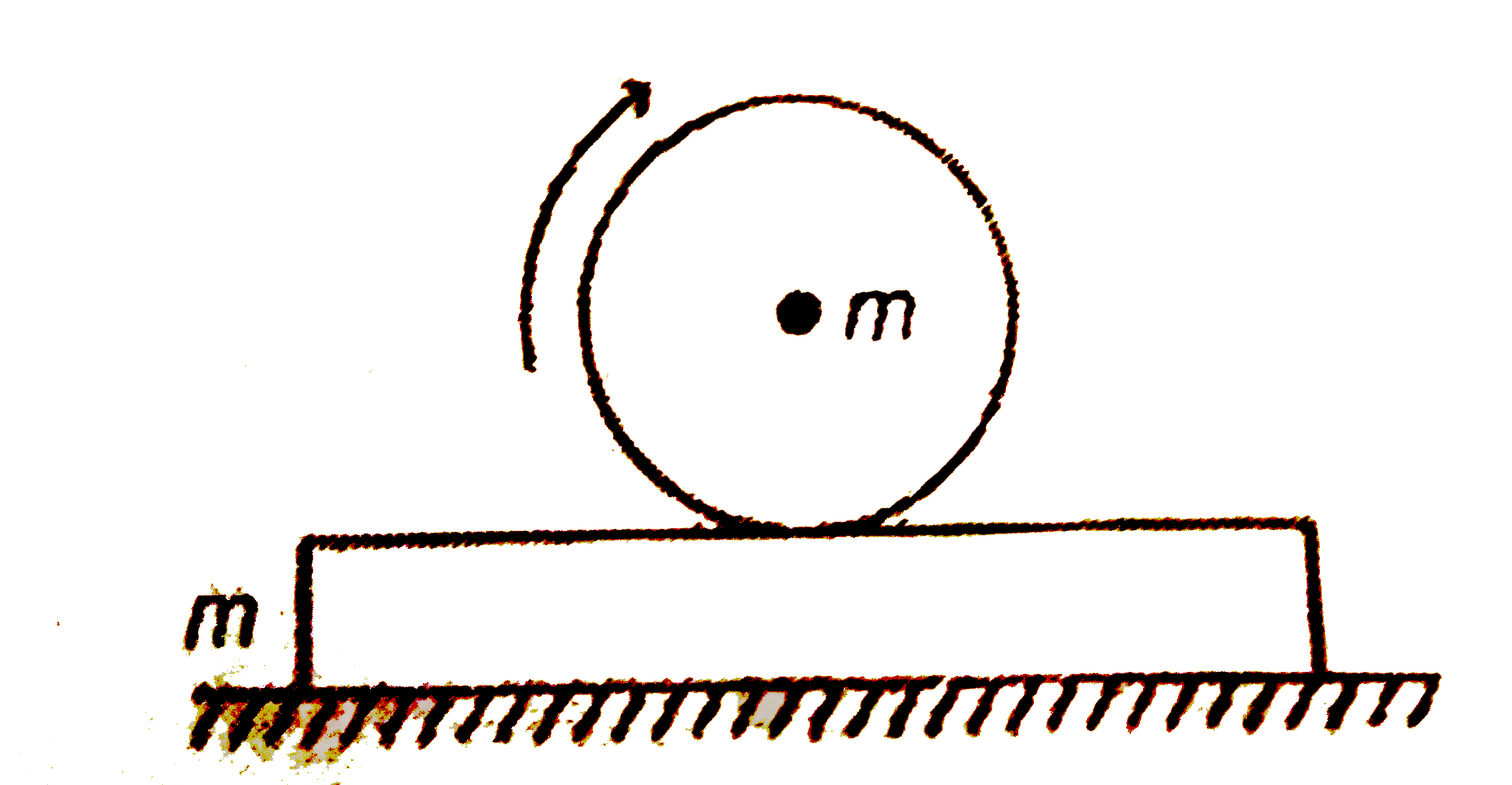
View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View Solution
