A light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to

2πR3ρg
2ρgR3
2R2ρg3
None of these
The correct Answer is:D
Step by step video & image solution for A light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density rho. The force F required to prevent the rotation of the gate is equal to by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
A square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is

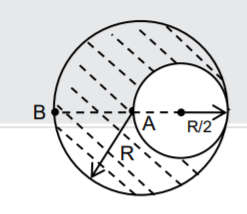
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View Solution
Knowledge Check
A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
AM gBMg−Vρ gCMg+ΠR2hgρDρg(V+ΠR2h)
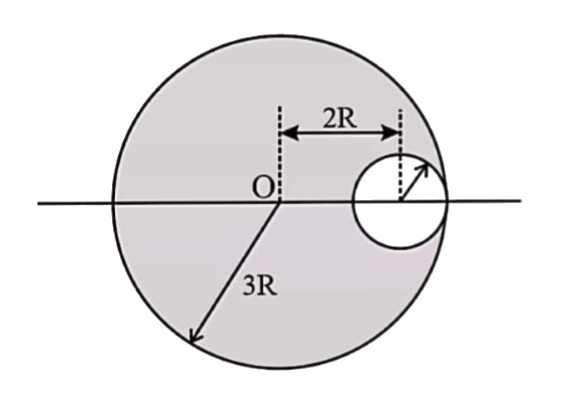
The figure shows a disc of radius 3R from which a circular hole of radius R is cut as shown in the figure. The distance of the centre of mass of the remaining object from the point O is
View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-
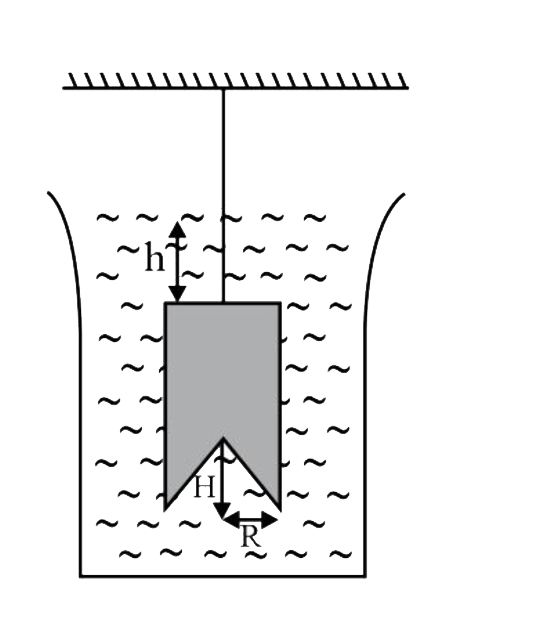
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
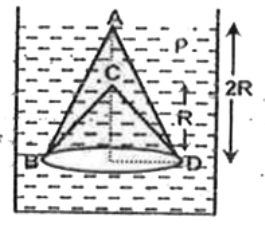
View SolutionA solid cone of uniform density and height 2R and base radius R has a conical portion scooped out form its base with the same base radius but height R as shown in the figure. The solid cone is floating in a liquid of density ρ with vertex A touching the fluid surface . If atomospheric pressure is P0 the force acting on the surface BCD due to liquid is
View SolutionA horizontal tube of uniform cross-sectional area A is bent in the form of U as shown in figure. If the liquid of density ρ enters and leaves the tube with velcity v, then the extermal force F requried to hold the bend stationary is

View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
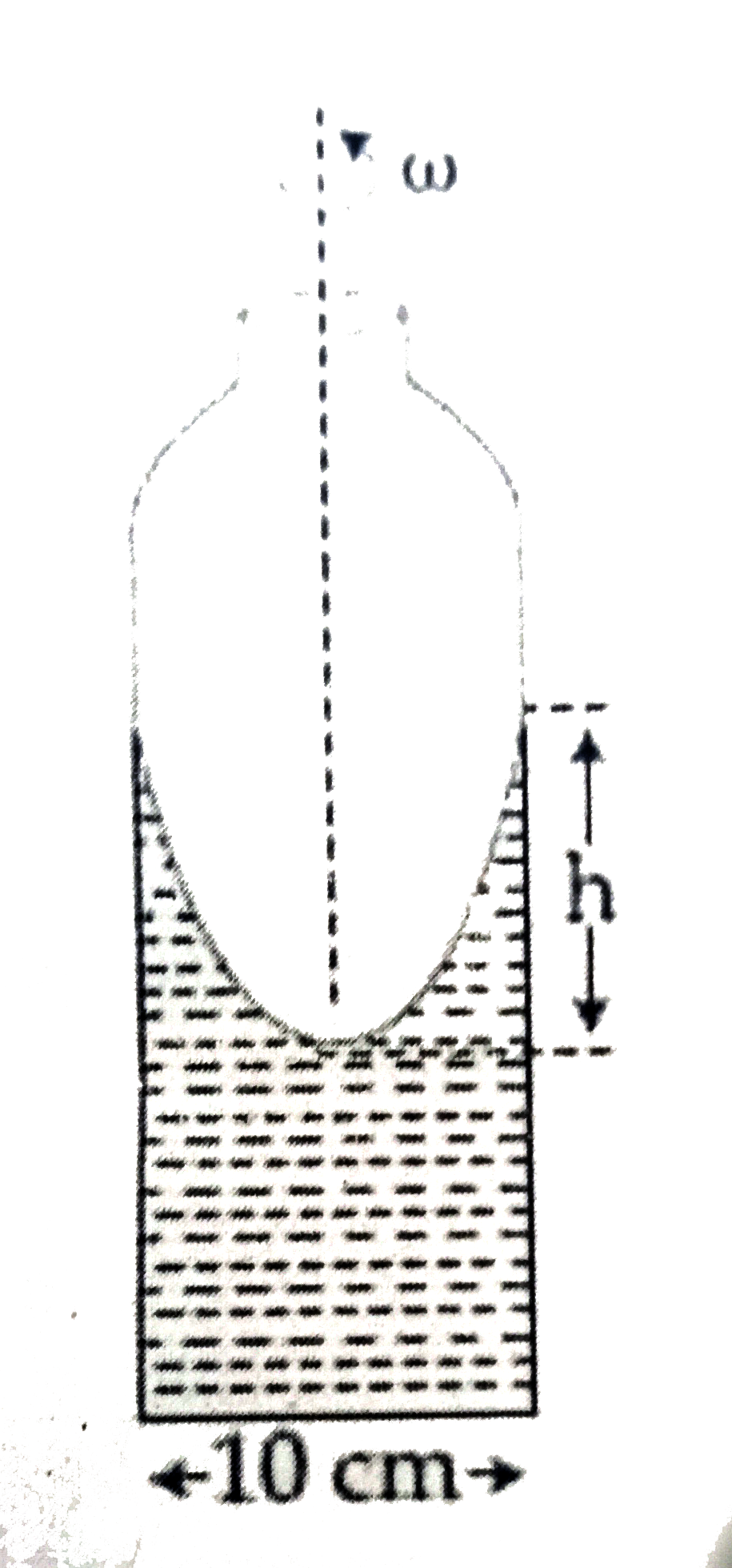
View SolutionA solid sphere of radius R is rolled by a force F acting at the topo of the sphere as shown in the figure. There is no slipping and initially sphere is in the rest position, then (CM= centre of mass)

View Solution
