The width of depletion region in p-n junction diode is 500nm and an intrinsic electric field of 6×105Vm−1 is also found to exist in it. What is the kinetic energy which a conduction electron must have in order to diffuse from the n-side to p-side?
0.30 V
0.40 V
3 V
4 V
The correct Answer is:A
To solve the problem, we need to find the kinetic energy that a conduction electron must have in order to diffuse from the n-side to the p-side of a p-n junction diode. The given parameters are the width of the depletion region (D) and the intrinsic electric field (E).
1. Identify the Given Values:
- Width of the depletion region (D) = 500 nm = 500×10−9 m
- Intrinsic electric field (E) = 6×105 V/m
2. Calculate the Potential Barrier (V):
The potential barrier across the depletion region can be calculated using the formula:
V=E×D
Substituting the values:
V=(6×105V/m)×(500×10−9m)
3. Perform the Calculation:
V=6×105×500×10−9
V=6×500×10−4
V=3000×10−4=0.30V
4. Determine the Kinetic Energy (K.E.):
The kinetic energy required for the conduction electron to overcome the potential barrier is given by:
K.E.=e×V
where e is the charge of an electron, approximately 1.6×10−19 C. Now substituting the values:
K.E.=(1.6×10−19C)×(0.30V)
5. Calculate the Kinetic Energy:
K.E.=1.6×10−19×0.30
K.E.=0.48×10−19J
6. Convert Kinetic Energy to Electron Volts (eV):
Since 1eV=1.6×10−19J:
K.E.=0.48×10−191.6×10−19eV
K.E.=0.30eV
Final Answer:
The kinetic energy required for a conduction electron to diffuse from the n-side to the p-side of the p-n junction diode is 0.30 eV.
- Width of the depletion region (D) = 500 nm = 500×10−9 m
- Intrinsic electric field (E) = 6×105 V/m
The potential barrier across the depletion region can be calculated using the formula:
V=E×D
Substituting the values:
V=(6×105V/m)×(500×10−9m)
V=6×105×500×10−9
V=6×500×10−4
V=3000×10−4=0.30V
The kinetic energy required for the conduction electron to overcome the potential barrier is given by:
K.E.=e×V
where e is the charge of an electron, approximately 1.6×10−19 C. Now substituting the values:
K.E.=(1.6×10−19C)×(0.30V)
K.E.=1.6×10−19×0.30
K.E.=0.48×10−19J
Since 1eV=1.6×10−19J:
K.E.=0.48×10−191.6×10−19eV
K.E.=0.30eV
The kinetic energy required for a conduction electron to diffuse from the n-side to the p-side of the p-n junction diode is 0.30 eV.
Topper's Solved these Questions
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Integer type questions
Explore 14 Videos
Similar Questions
In a p-n junction, the depletion region is 400nm wide and and electric field of 5×105Vm−1exists in it (a)Find the height of the potential barrier, (b)What should be the minimum kinetic energy of a conduction electron which can diffuse from the n-side to the p-side?
View SolutionWhat's the reason that In an unbiased n-p junction , electrons diffuse from n-region to p-region :
View Solution
Knowledge Check
If an electron approaches the p-n junction from the n-side with a speed of 5×105ms−1 ,with what speed will it enter the p-side?
A5×105 m/sB2.5×106 m/sC2.7×105 m/sD1×105 m/s
The ionisation potential of mercury is 10.39 V. How far an electron must travel in an electric field of 1.5×106V/m to gain sufficient energy to ionise mercury ?
View SolutionAn electron accelerated by a potential difference 2.5 kV moves horizontally into a region of space in which there is a downward directed uniform electric field of magnitude 10kVm−1.
(a) In what direction must a magnetic field be applied so that the electron moves undeflected? Ignore the gravitational force. What is the magnitude of the smallest magnetic field possible in this case?
(b) What happens if the charge is a proton that passes through the same combination of fields ?
View SolutionIn a p−n junction diode having depletion layer of thickness 10−6m, the potential across it is 0.1V. The electric field produced is
View SolutionIn a p−n junction diode having depletion layer of thickness 10−6m, the potential across it is 1V. The electric field produced is
View SolutionIn a p-n junction, the thickness of depletion region is 2×10−7m and potential barrier across the junction is 0.20 V
What will be the intensity of electric field in this region ?
View SolutionIn a p-n junction,a potential barrier of 250 mev exsists across the junction.A hole with a kimetic energy of 300 meV approaches the junction. Find the kinetic energy of the hole when it crosses the junction if the hole approached the junction (a)from the p-side and (b)from the n-side.
View Solution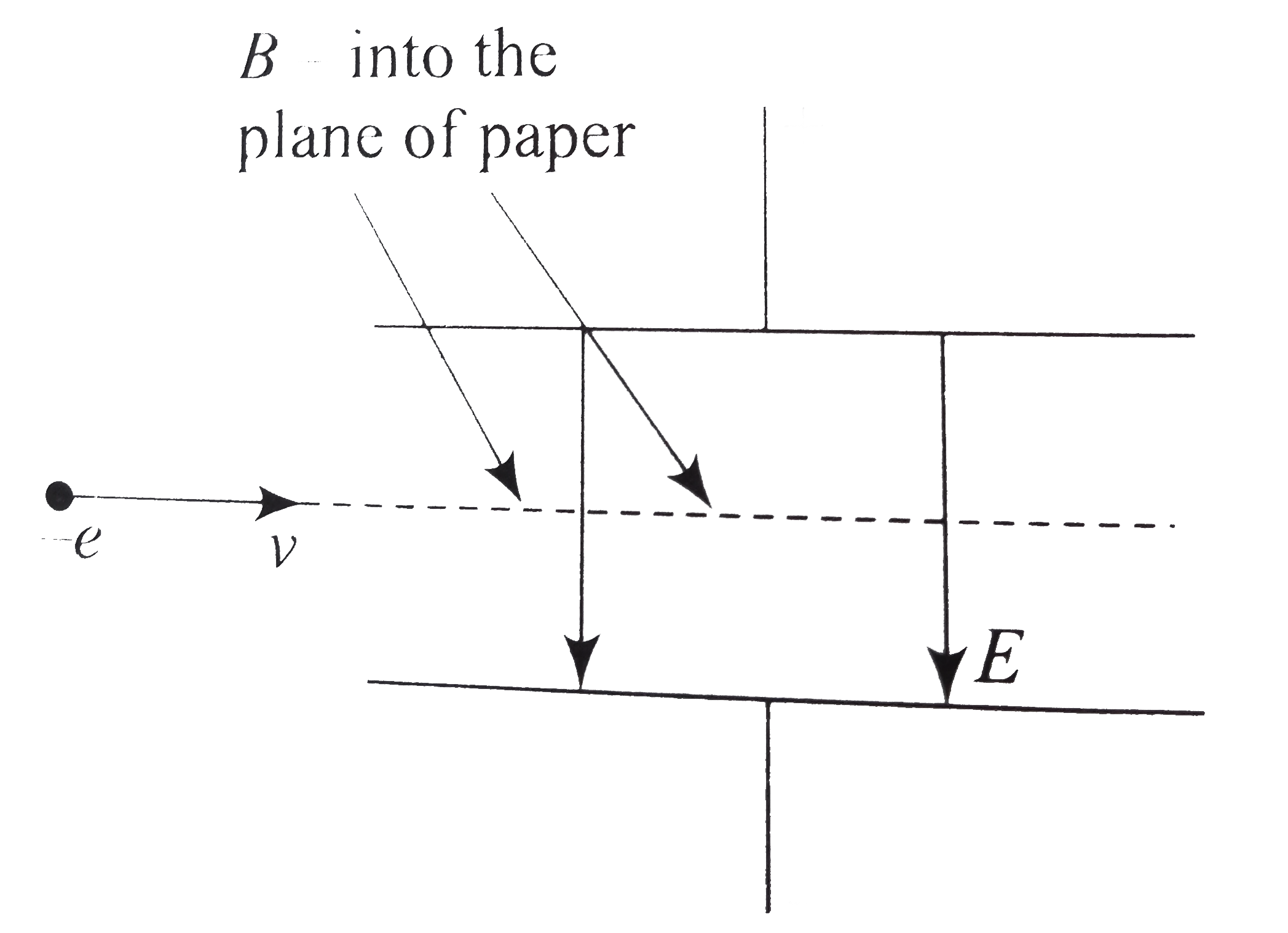
Electrons taveling at a velocity of 2.4×106ms−1 enter a region of crossed electric and magnetic fields as shoen in Fig. If the electric field is 3.0×106 Vm and the flux density of the magnetic field is 1.5 T, the electrons upon entering the region of the crossed fields will
View Solution