A cocave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is 1/4. the focal length of the lens will be
8.6 cm
6.2 cm
10 cm
4.4 cm
The correct Answer is:D
To solve the problem step by step, we will use the information provided about the concave lens, the distance between the object and image, and the magnification.
1. Understanding the Problem:
We have a concave lens that forms a virtual image of an object. The distance between the object and the image is given as 10 cm. The magnification (M) produced by the lens is 14.
2. Setting Up Variables:
- Let the image distance (V) be −x (negative because the image is virtual).
- The object distance (U) can be expressed as −x+10 (negative because it is on the same side as the object).
3. Using the Magnification Formula:
The magnification (M) for a lens is given by:
M=VU
Substituting the values we have:
14=−x−x+10
4. Cross-Multiplying:
Cross-multiplying gives:
−x+10=4(−x)
Simplifying this:
−x+10=−4x
5. Rearranging the Equation:
Rearranging gives:
10=−4x+x
10=−3x
x=−103
6. Finding Object Distance (U):
Now substituting x back to find U:
U=−x+10=−(−103)+10=103+10=103+303=403
7. Finding Image Distance (V):
The image distance is:
V=−x=−(−103)=103
8. Using the Lens Formula:
The lens formula is given by:
1f=1V−1U
Substituting the values of V and U:
1f=1−103−1−403
This simplifies to:
1f=−310+340
9. Finding a Common Denominator:
The common denominator is 40:
1f=−1240+340=−12−340=−940
10. Calculating Focal Length (f):
Therefore, we have:
f=−409≈−4.44 cm
Conclusion:
The focal length of the concave lens is approximately −4.44 cm.
We have a concave lens that forms a virtual image of an object. The distance between the object and the image is given as 10 cm. The magnification (M) produced by the lens is 14.
- Let the image distance (V) be −x (negative because the image is virtual).
- The object distance (U) can be expressed as −x+10 (negative because it is on the same side as the object).
The magnification (M) for a lens is given by:
M=VU
Substituting the values we have:
14=−x−x+10
Cross-multiplying gives:
−x+10=4(−x)
Simplifying this:
−x+10=−4x
Rearranging gives:
10=−4x+x
10=−3x
x=−103
Now substituting x back to find U:
U=−x+10=−(−103)+10=103+10=103+303=403
The image distance is:
V=−x=−(−103)=103
The lens formula is given by:
1f=1V−1U
Substituting the values of V and U:
1f=1−103−1−403
This simplifies to:
1f=−310+340
The common denominator is 40:
1f=−1240+340=−12−340=−940
Therefore, we have:
f=−409≈−4.44 cm
The focal length of the concave lens is approximately −4.44 cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
The distance between an object and its upright image is 20cm. if the magnification is 0.5, what is the focal length of the lens that is being used to form the image?
View SolutionA convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View Solution
Knowledge Check
A concave lens forms the image of an object such that the distance between the object and image is 10cm and the magnification produced is 1/4. The focal length of the lens will be
A−6.2cmB−4.4cmC−8.6cmD−10cmAn object is place 20 cm from a diverging lens. If the distance between the lens and the image is 8 cm, what is the magnification?
A115B25C12D2An object is placed at a distance of 1.5m from a screen and a convex lens is interposed between them. The magnification produced is 4. What is the focal length of the lens ?
A1mB0.5mC0.24mD2m
A convex lens of focal length f is placed somewhere in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal lnegth oof the lens is .
View SolutionAn object is placed at a distance u from an equiconvex lens such that the distannce between the object and its real image is minimum. The focal length of the lens is f. The value of u is
View SolutionAn extended real object of size 2cm is palced perpendicular to the principle axis of a converging lens of focal length 20cm. The distance between the object and the lens is 30cm
(i) Find the laterial magnification produced by the lens.
(ii) Find the height of the image.
View SolutionThe graph shown relationship between object distance and image distance for a equiconvex lens. Then focal length of the lens is
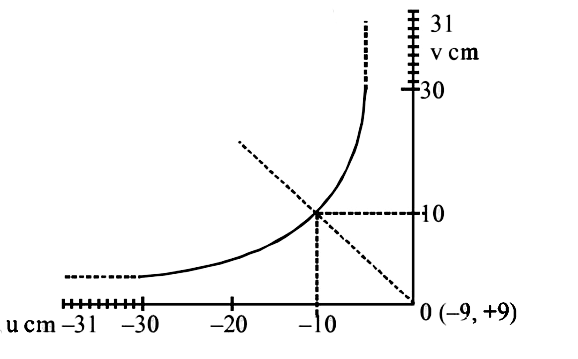
View SolutionWhen an object is at distances x and y from a lens, a real image and a virtual image is formed respectively having same magnification. The focal length of the lens is
View Solution