For a concave mirror of focal length f, image is 2 times larger. Then the object distance from the mirror can be
virtual image is always larger in size
real image is always smaller in size
real image is always larger in size
real image may be smaller or larger in size
The correct Answer is:A, D
To find the object distance from a concave mirror when the image is 2 times larger than the object, we can follow these steps:
1. Understand the Magnification:
The magnification (m) is given as 2. For mirrors, magnification is defined as:
m=−vu
where v is the image distance and u is the object distance. Since the image is 2 times larger, we can write:
m=±2
Therefore, we have:
−vu=±2
2. Set Up the Two Cases:
We can consider two cases based on the magnification:
- Case 1: m=2 (real image)
- Case 2: m=−2 (virtual image)
3. Case 1: Real Image (m = 2):
From the magnification formula:
−vu=2⟹v=−2u
Now, we use the mirror formula:
1f=1v+1u
Substituting v=−2u:
1f=1−2u+1u
Simplifying this:
1f=−12u+22u=12u
Therefore:
f=2u⟹u=f2
4. Case 2: Virtual Image (m = -2):
From the magnification formula:
−vu=−2⟹v=2u
Again, using the mirror formula:
1f=1v+1u
Substituting v=2u:
1f=12u+1u
Simplifying this:
1f=12u+22u=32u
Therefore:
f=2u3⟹u=3f2
5. Final Results:
The object distance can be:
- u=f2 (for the real image)
- u=3f2 (for the virtual image)
Summary:
The object distance from the mirror can be either f2 or 3f2.
The magnification (m) is given as 2. For mirrors, magnification is defined as:
m=−vu
where v is the image distance and u is the object distance. Since the image is 2 times larger, we can write:
m=±2
Therefore, we have:
−vu=±2
We can consider two cases based on the magnification:
- Case 1: m=2 (real image)
- Case 2: m=−2 (virtual image)
From the magnification formula:
−vu=2⟹v=−2u
Now, we use the mirror formula:
1f=1v+1u
Substituting v=−2u:
1f=1−2u+1u
Simplifying this:
1f=−12u+22u=12u
Therefore:
f=2u⟹u=f2
From the magnification formula:
−vu=−2⟹v=2u
Again, using the mirror formula:
1f=1v+1u
Substituting v=2u:
1f=12u+1u
Simplifying this:
1f=12u+22u=32u
Therefore:
f=2u3⟹u=3f2
The object distance can be:
- u=f2 (for the real image)
- u=3f2 (for the virtual image)
The object distance from the mirror can be either f2 or 3f2.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Matrix matching type Q.
8 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
The image of an object placed on the principal axis of a concave mirror of focal length 12 cm is formed at a point which is 10cm more distance form the mirror than the object. The magnification of the image is
View SolutionAn infinitely long rod lies along the axis of a concave mirror of focal length f. The near end of the rod is distance u>f from the mirror. Its image will have length
View SolutionA point object is moving on the principal axis of a concave mirror of focal length 24cm towards the mirror. When it is at a distance of 60cm from the mirror, its velocity is . 9sec/cm What is the velocity of the image at that instant
View SolutionWe wish to obtain an erect image of an object, using a concave mirror of focal length 15 cm. What should be the range of distance of the object from the mirror? What is the nature of the image? Is the image larger or smaller than the object? Draw a ray diagram to show the image formation in this case.
View SolutionA convex mirror offocal length fforms an image which is 1/n times the object. The distance of the object from the mirror is:
View SolutionAn object is placed in front of a concave mirror of focal length f as shown in figure. Choose the correct shape of the image.

View SolutionThe image formed by a convex mirror of focal length 30cm. is a quarter of the object. What is the distance of the object from the mirror ?
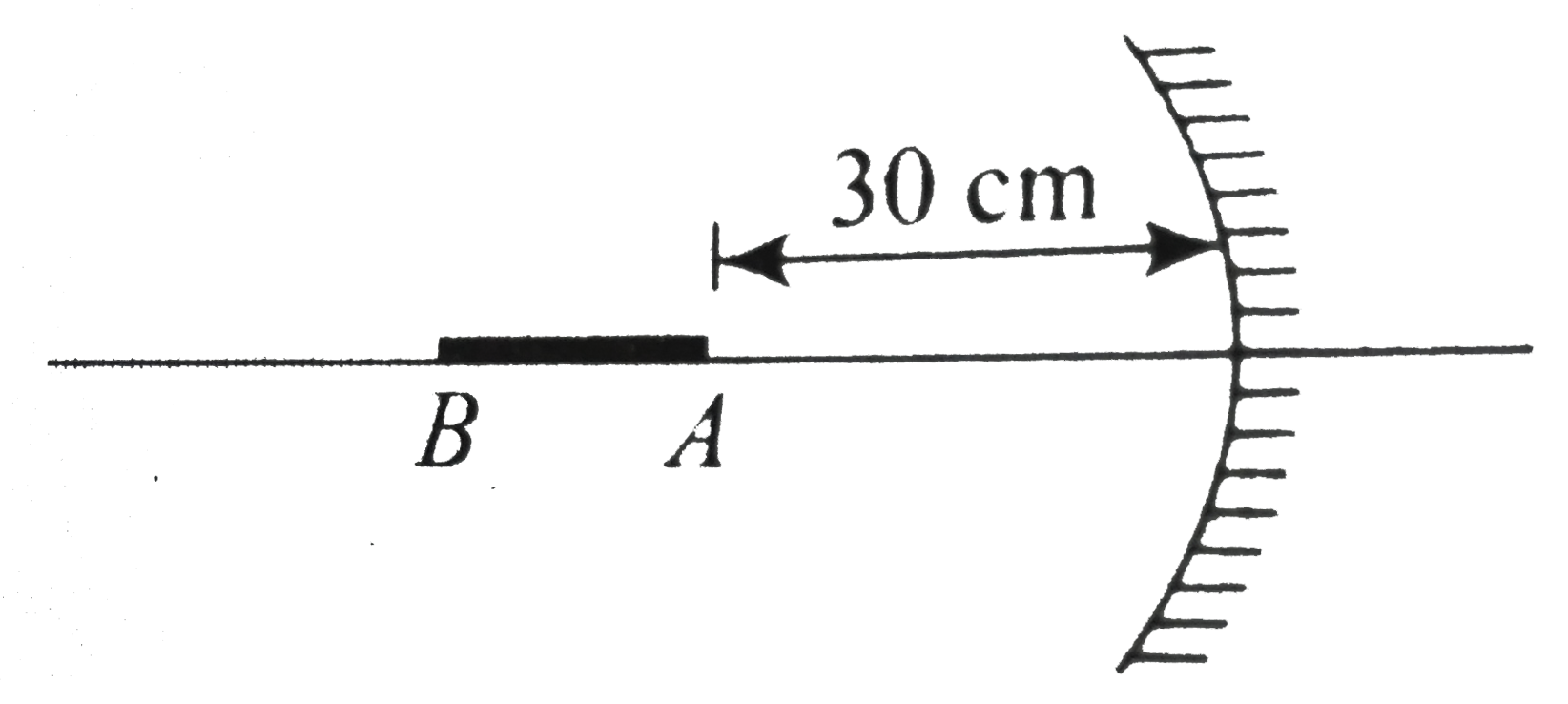
View SolutionObject AB is placed on the axis of a concave mirror of focal length 10cm. End A of the object is at 30cm from the mirror. Find the length of the image
a. if length of object is 5cm.
b. if length of object is 1 mm.
View SolutionAn object is moving towards a concave mirror of focal length 24 cm. When it is at a distance of 60 cm from the mirror, its speed is 9cm/s. The speed of its image at that instant , is
View SolutionA concave mirror of focal length f produces a real image n times the size of the object. What is the distance of the object from the mirror?
View Solution
