Two particles are held in equilibrium by the gravitational and electrostatic forces between them. Particle-A has mass mα and charge qα and particle-B has mass mb and charge qb. The distance between the charges may cause the chages to accelerate towards one another ?
ma is doubled and mb is halved
ma is doubled and mb is doubled
qa is doubled and qb is doubled
d is doubled
The correct Answer is:B
To analyze the equilibrium of two charged particles held by gravitational and electrostatic forces, we can follow these steps:
1. Understand the Forces Involved:
- The two particles, A and B, experience gravitational force (FG) and electrostatic force (FE).
- The gravitational force is given by:
FG=Gmαmbd2
- The electrostatic force is given by:
FE=k|qαqb|d2
- Here, G is the gravitational constant, k is Coulomb's constant, mα and mb are the masses of particles A and B, respectively, qα and qb are their charges, and d is the distance between them.
2. Set the Forces Equal for Equilibrium:
- For the particles to be in equilibrium, the magnitudes of the forces must be equal:
FG=FE
- This leads to the equation:
Gmαmbd2=k|qαqb|d2
- The d2 cancels out, simplifying to:
Gmαmb=k|qαqb|
3. Consider Changes in Mass and Charge:
- We need to analyze how changes in mass and charge affect the forces.
- If we change the masses or charges, we can determine if the balance is disturbed.
4. Evaluate Each Option:
- Option A: If mα is doubled and mb is halved:
- New gravitational force:
F′G=G(2mα)(12mb)d2=Gmαmbd2
- Electrostatic force remains unchanged. Thus, no acceleration occurs.
- Option B: If both mα and mb are doubled:
- New gravitational force:
F′G=G(2mα)(2mb)d2=4Gmαmbd2
- This will be greater than the electrostatic force, causing acceleration towards each other.
- Option C: If both qα and qb are doubled:
- New electrostatic force:
F′E=k(2qα)(2qb)d2=4k|qαqb|d2
- This will not cause acceleration as both forces increase equally.
- Option D: If d is doubled:
- Both forces decrease by a factor of 4, maintaining equilibrium.
5. Conclusion:
- The only option that causes the charges to accelerate towards each other is Option B where both masses are doubled.
- The two particles, A and B, experience gravitational force (FG) and electrostatic force (FE).
- The gravitational force is given by:
FG=Gmαmbd2
- The electrostatic force is given by:
FE=k|qαqb|d2
- Here, G is the gravitational constant, k is Coulomb's constant, mα and mb are the masses of particles A and B, respectively, qα and qb are their charges, and d is the distance between them.
- For the particles to be in equilibrium, the magnitudes of the forces must be equal:
FG=FE
- This leads to the equation:
Gmαmbd2=k|qαqb|d2
- The d2 cancels out, simplifying to:
Gmαmb=k|qαqb|
- We need to analyze how changes in mass and charge affect the forces.
- If we change the masses or charges, we can determine if the balance is disturbed.
- Option A: If mα is doubled and mb is halved:
- New gravitational force:
F′G=G(2mα)(12mb)d2=Gmαmbd2
- Electrostatic force remains unchanged. Thus, no acceleration occurs.
- Option B: If both mα and mb are doubled:
- New gravitational force:
F′G=G(2mα)(2mb)d2=4Gmαmbd2
- This will be greater than the electrostatic force, causing acceleration towards each other.
- Option C: If both qα and qb are doubled:
- New electrostatic force:
F′E=k(2qα)(2qb)d2=4k|qαqb|d2
- This will not cause acceleration as both forces increase equally.
- Option D: If d is doubled:
- Both forces decrease by a factor of 4, maintaining equilibrium.
- The only option that causes the charges to accelerate towards each other is Option B where both masses are doubled.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
The charges +4q and +q are at a distance 3m apart. At what point between the charges, a third charge +q must be placed to keep it in equilibrium ?
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
View Solution
Knowledge Check
If the distance between two point particles is doubled, then the gravitational force between them
Adecreases by a factor of 4Bdecreases by a factor of 2Cincreases by a factor of 2Dincreases by a factor of 4Two particles have unequal charges, one is +q and the other is -2q. The strength of the electrostatic force between these two stationary particles is equal to F. what happens of F if the distance between the particles is halved?
AIt decreases by a factor of 4Bit decreases by a factor of 2.Cit remains the same.Dit increases by a factor of 4.
Two particles having charge Q1 and Q2 , when kept at a certain distance exert a force F on each other . If the distance between the two particles is reduced to half and the charge on each particle is doubled , the force between the particles would be
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA charge Q is divided into two charge q and Q-q. The value of q such that the force between them is maximum is
View SolutionAn electrostatic field line leaves at angle α from charge q1 and connects with point charge −q2 at angle β (see figure).
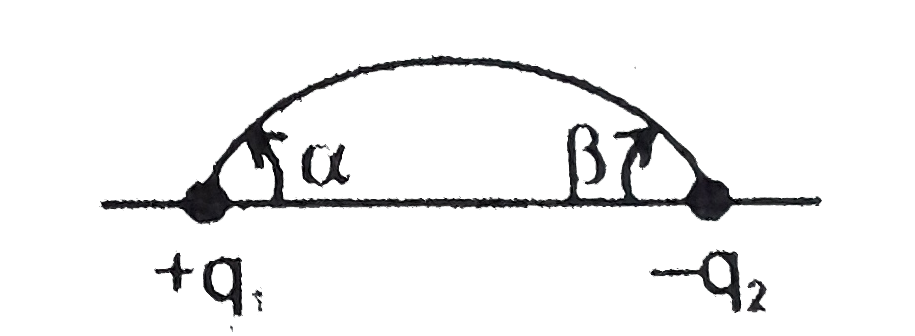
then find the relationship between α and β :
View SolutionTwo particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. If particle C is displaced through a distance x along the line AB. What will be the time period of the oscillations.
View SolutionTwo particle of equal mass m and charge q are placed at a distance of 16 cm. They do not experience any force. The value of qm is
View Solution
