Three large conducting plates carrying charges Q,2Qand3Q on them, are placed parallel to each other as shown in the figure. If U1andU2 denote electrostatic potential energy in the space between 1st and 2nd plane and 2nd and 3rd plate respectively as indicated, then U2U1 equals
1
0
2/3
3/2
The correct Answer is:B
To solve the problem, we need to find the ratio of the electrostatic potential energy U2 between the second and third plates to the electrostatic potential energy U1 between the first and second plates.
1. Identify the Charges on the Plates:
- Let the charges on the plates be Q1=Q, Q2=2Q, and Q3=3Q.
2. Determine the Electric Field Between the Plates:
- The electric field E between two charged plates can be calculated using the formula:
E=σϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
- For the first and second plates, the net electric field E1−2 can be calculated as:
E1−2=QAϵ0+2QAϵ0=3QAϵ0
- For the second and third plates, the net electric field E2−3 is:
E2−3=2QAϵ0+3QAϵ0=5QAϵ0
3. Calculate the Potential Energy:
- The electrostatic potential energy U in a region between two plates can be expressed as:
U=12CV2
where C is the capacitance and V is the potential difference.
- The potential difference V between two plates is given by:
V=E⋅d
where d is the distance between the plates.
- Thus, for U1 (between plates 1 and 2):
U1=12(Qϵ0)(3QAϵ0⋅d1)2
- For U2 (between plates 2 and 3):
U2=12(2Qϵ0)(5QAϵ0⋅d2)2
4. Find the Ratio U2U1:
- The ratio of the potential energies can be simplified:
U2U1=12(2Qϵ0)(5QAϵ0⋅d2)212(Qϵ0)(3QAϵ0⋅d1)2
- Canceling out common terms and simplifying gives:
U2U1=2⋅25d221⋅9d21=50d229d21
5. Conclusion:
- The final ratio of the electrostatic potential energies U2U1 depends on the distances d1 and d2 between the plates.
- Let the charges on the plates be Q1=Q, Q2=2Q, and Q3=3Q.
- The electric field E between two charged plates can be calculated using the formula:
E=σϵ0
where σ is the surface charge density and ϵ0 is the permittivity of free space.
- For the first and second plates, the net electric field E1−2 can be calculated as:
E1−2=QAϵ0+2QAϵ0=3QAϵ0
- For the second and third plates, the net electric field E2−3 is:
E2−3=2QAϵ0+3QAϵ0=5QAϵ0
- The electrostatic potential energy U in a region between two plates can be expressed as:
U=12CV2
where C is the capacitance and V is the potential difference.
- The potential difference V between two plates is given by:
V=E⋅d
where d is the distance between the plates.
- Thus, for U1 (between plates 1 and 2):
U1=12(Qϵ0)(3QAϵ0⋅d1)2
- For U2 (between plates 2 and 3):
U2=12(2Qϵ0)(5QAϵ0⋅d2)2
- The ratio of the potential energies can be simplified:
U2U1=12(2Qϵ0)(5QAϵ0⋅d2)212(Qϵ0)(3QAϵ0⋅d1)2
- Canceling out common terms and simplifying gives:
U2U1=2⋅25d221⋅9d21=50d229d21
- The final ratio of the electrostatic potential energies U2U1 depends on the distances d1 and d2 between the plates.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced
44 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Comprehension
36 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Medical entrances s gallery
21 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
Similar Questions
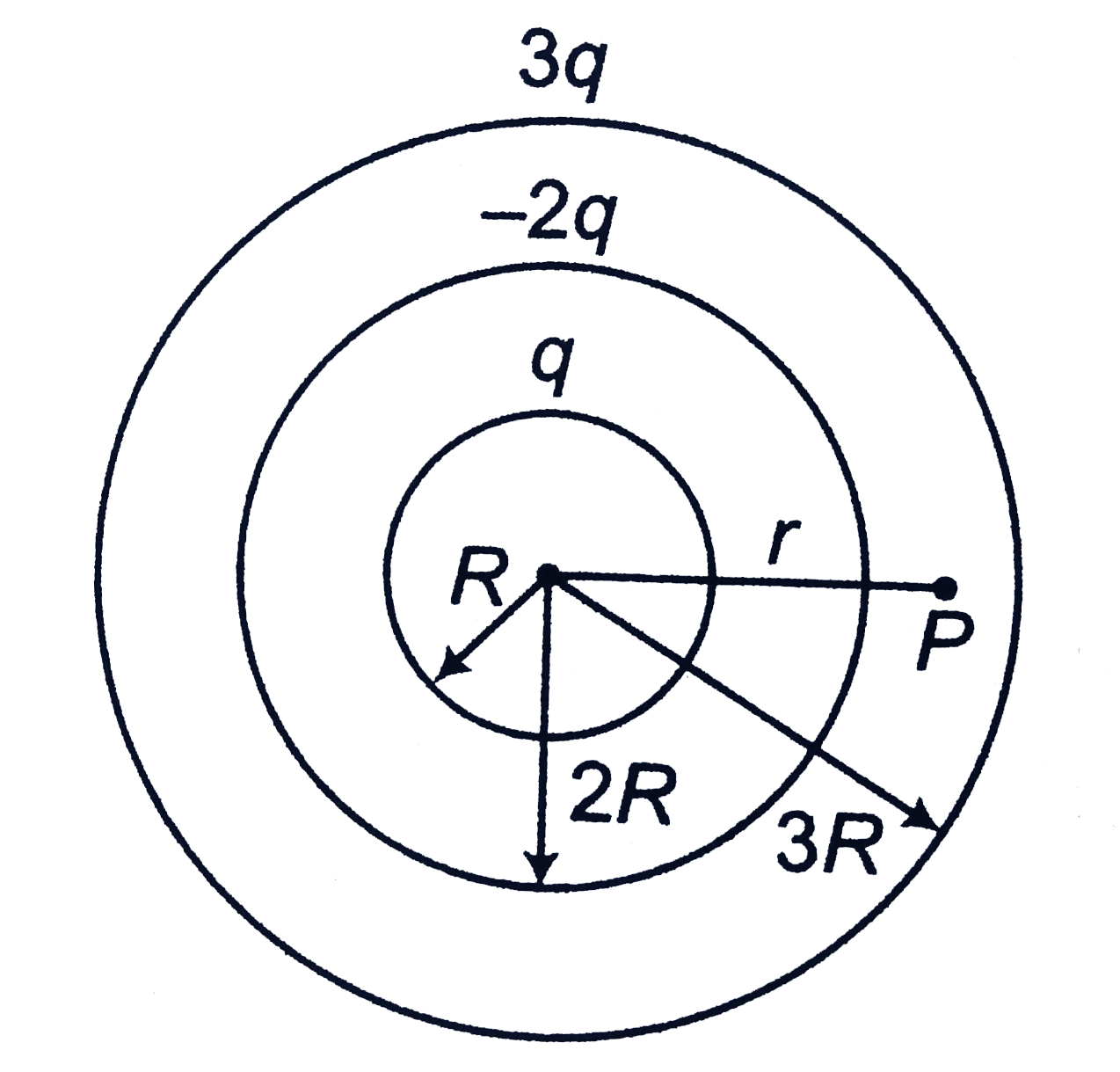
Three conducting spherical shells have charges q,−2q and 3q as shown in figure. Find electric Potential at point P as shown in figure.
View SolutionThree charged particles are initially in position 1, "They are free to move and they come in position" 2 "after some time. Let" U1 and U2 be the electrostatic potential energies in position 1and2. Then
View SolutionThree large identical conducting parallel plates carrying charge +Q,−Q,and+2Q, respectively, are placed as shown in figure. If EA,Eb,andEC refer to the magnitudes of the electric field at points A, B, and C, respectively. Then
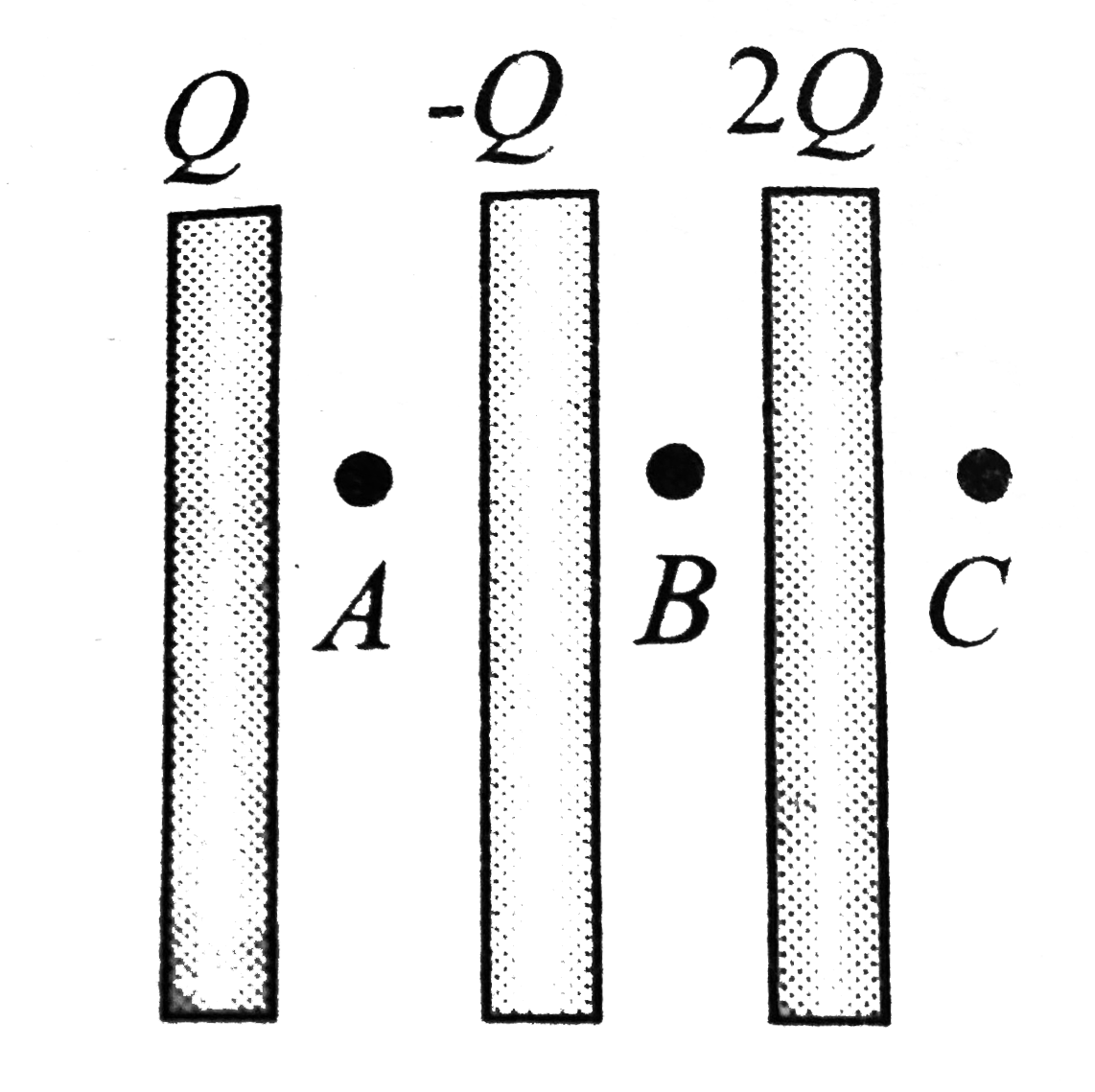
View SolutionForce between two conducting large plates , with charges Q and Q2 as shown in the figure, is (Area of each face of plate =A)
_PHY_E01_022_Q01.png)
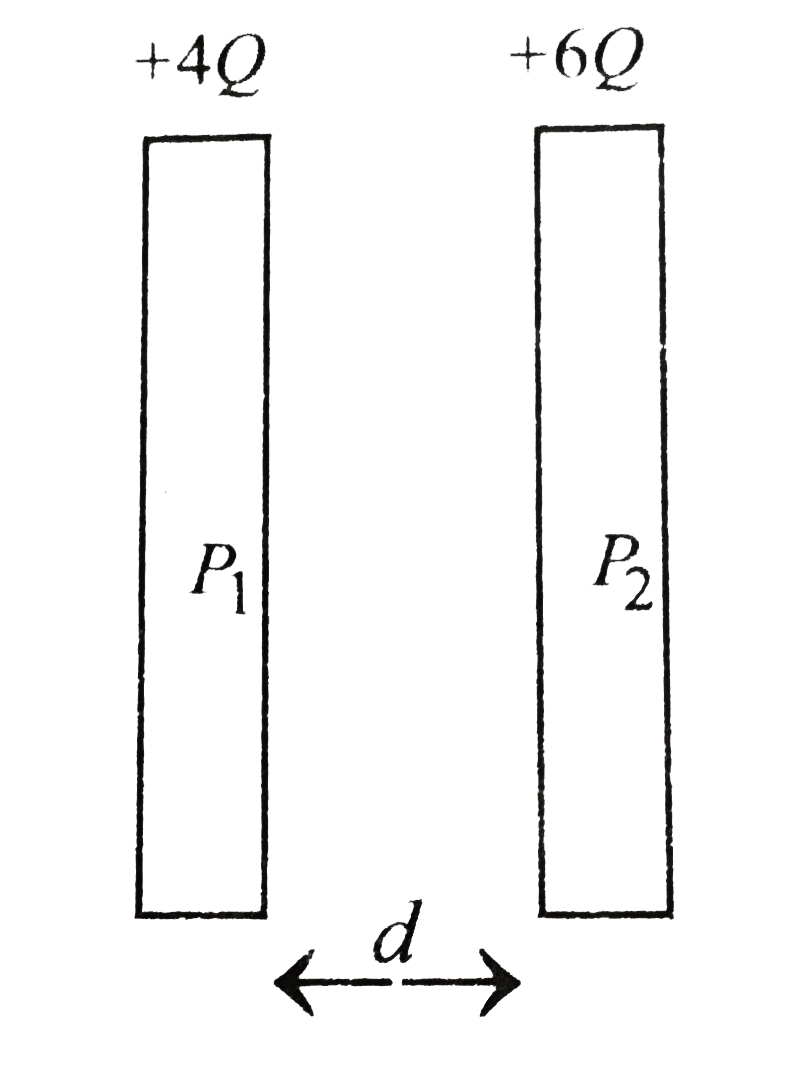
View SolutionTwo identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
View SolutionTwo conducting plates M and N, each having large surface area A (on one side), are placed parallel to each other in figure. The plate M is given charge Q1 and N, charge Q2(<Q1). Then

View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge. Q1 and B a charge Q2. Find the distribution of charges on the four surface.
View SolutionThree large conducting sheets placed parallel to each other at a finite distance contain charges Q,−2Q,and3Q, respectively. Find the electric fields at points A, B, C, and D.
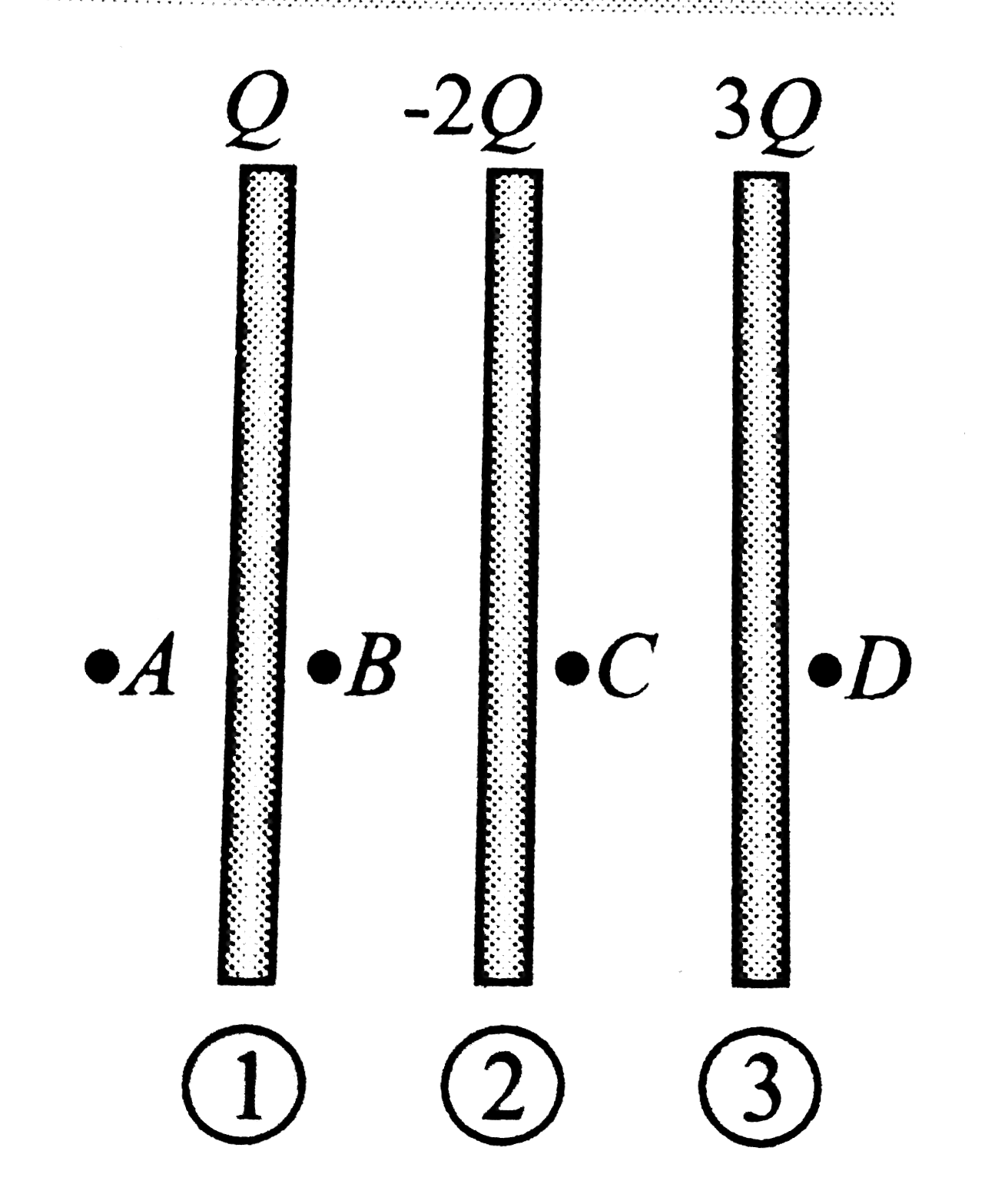
View SolutionTwo conducting plates A and B are placed parallel to each other. A is given a charge Q1 and B a charge Q2. Prove that the charges on the inner surfaces are of equal magnitude and opposite sign.
View SolutionTwo nonconducting infinite planes sheets having charges Q and 2Q are placed parallel to each other as shown in figure. The charge distribution on the four faces of the two plates is also shown. The electric field intensities at three points 1, 2, and 3 are →E1,→E2,and→E3, respectively. Then the magnitudes of →E1,→E2,and→E3 are, respectively (surface area of plates ) :

View Solution
