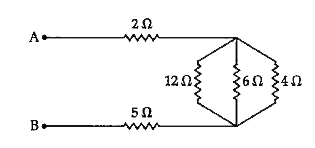
In the same figure, equivalent resistance between points A and D is
R4
2R
R
R2
The correct Answer is:D
To find the equivalent resistance between points A and D, we can follow these steps:
1. Identify the Configuration:
- We need to analyze the circuit configuration between points A and D. Assume that there are resistances connected in series and parallel.
2. Label the Points:
- Label the points in the circuit for clarity. Let's assume A, B, C, and D are the relevant points in the circuit.
3. Determine the Resistance Values:
- From the information provided, we assume that the resistance between points A and C is 2 ohms, and the resistance between points B and C is also 2 ohms.
4. Combine Resistors in Series and Parallel:
- If resistors are in series, their resistances add up. If they are in parallel, the equivalent resistance Req can be calculated using the formula:
1Req=1R1+1R2+…
- For example, if there are two resistors of 2 ohms each in parallel, the equivalent resistance would be:
Req=2×22+2=1 ohm
5. Calculate the Total Resistance:
- Continue combining resistances until you find the total equivalent resistance between points A and D.
6. Final Calculation:
- After calculating the equivalent resistances step by step, you will arrive at the final equivalent resistance between points A and D.
Conclusion:
- The equivalent resistance between points A and D can be found through careful analysis of the circuit, combining resistances in series and parallel as necessary.
- We need to analyze the circuit configuration between points A and D. Assume that there are resistances connected in series and parallel.
- Label the points in the circuit for clarity. Let's assume A, B, C, and D are the relevant points in the circuit.
- From the information provided, we assume that the resistance between points A and C is 2 ohms, and the resistance between points B and C is also 2 ohms.
- If resistors are in series, their resistances add up. If they are in parallel, the equivalent resistance Req can be calculated using the formula:
1Req=1R1+1R2+…
- For example, if there are two resistors of 2 ohms each in parallel, the equivalent resistance would be:
Req=2×22+2=1 ohm
- Continue combining resistances until you find the total equivalent resistance between points A and D.
- After calculating the equivalent resistances step by step, you will arrive at the final equivalent resistance between points A and D.
- The equivalent resistance between points A and D can be found through careful analysis of the circuit, combining resistances in series and parallel as necessary.
Topper's Solved these Questions
Similar Questions
Equivalent resistance between points A and B is
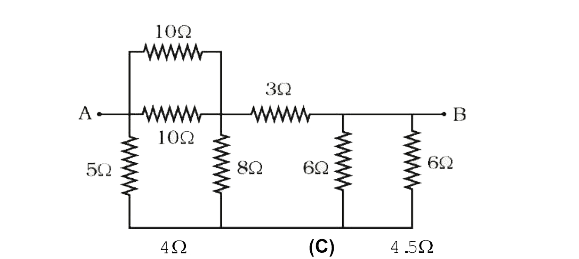
View SolutionThe equivalent resistance between points A and B
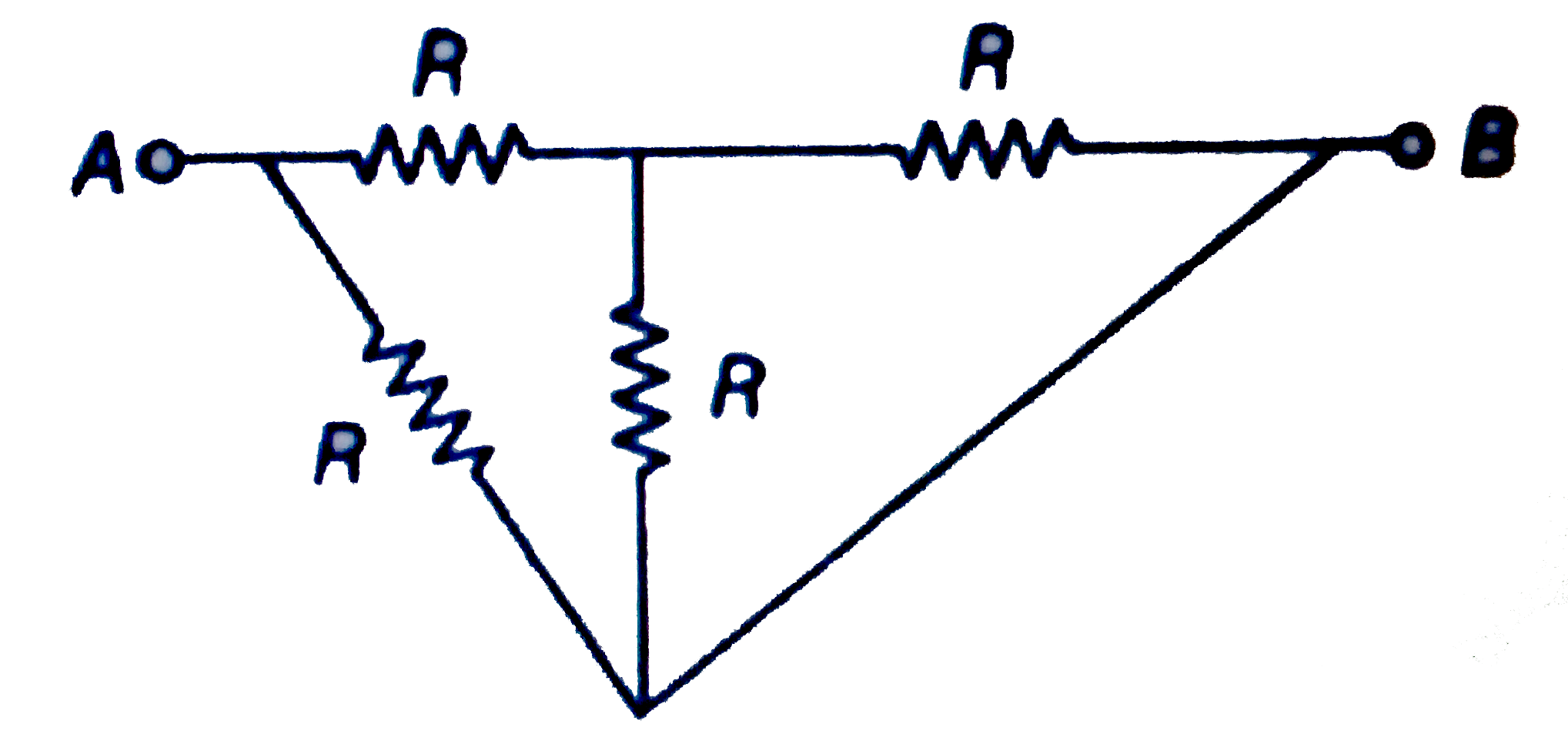
View SolutionThe equivalent resistance between points A and B is

View SolutionThe equivalent resistance between points A and B

View SolutionThe equivalent resistance between points A and B is

View SolutionIn the given figure, equivalent resistance between points P and Q is
View SolutionThe equivalent resistance between the points A and B is:
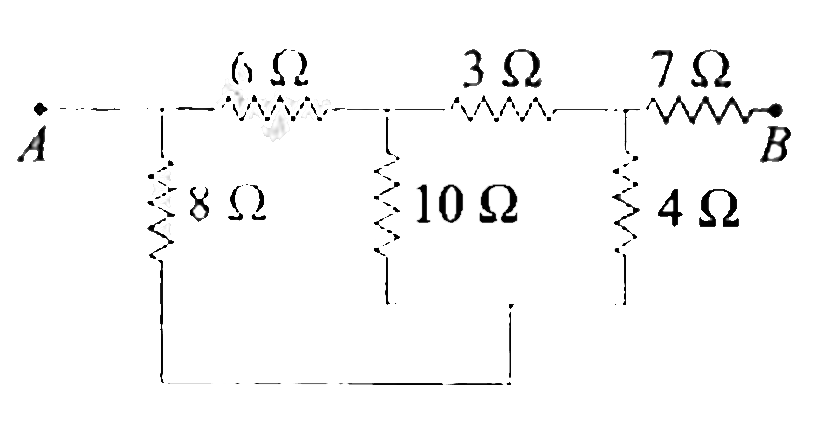
View SolutionFive resistance are connected as shown in the figure. The equivalent resistance between points A and C is
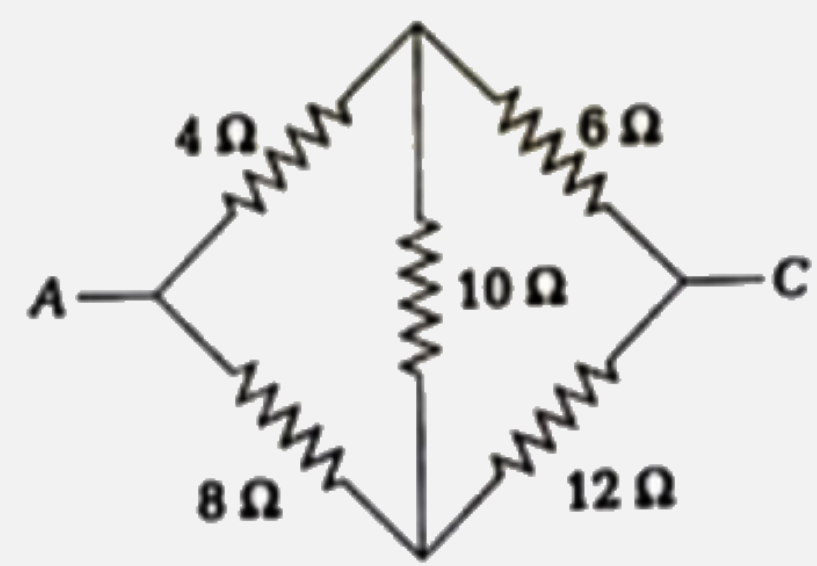
View SolutionFind the equivalent resistance between points A and B

View SolutionFind the equivalent resistance between points A and B.
View Solution

