Four moles of an ideal gas is initially in a state A having pressure and temperature 200 K . Keeping pressure constant the gas is taken to state B at temperature of 400K. The gas is then taken to a state C in such a way that its temperature increases and volume decreases. Also from B to C, the magnitude of increases. The volume of gas at state C is eaual to its volume at state A. Now gas is taken is initial state A keeping volume constant. A total of 1000 J heat is rejected from the sample in the cyclic process. Take .
Which graph between temperture T and volume V for the cyclic process is correct.
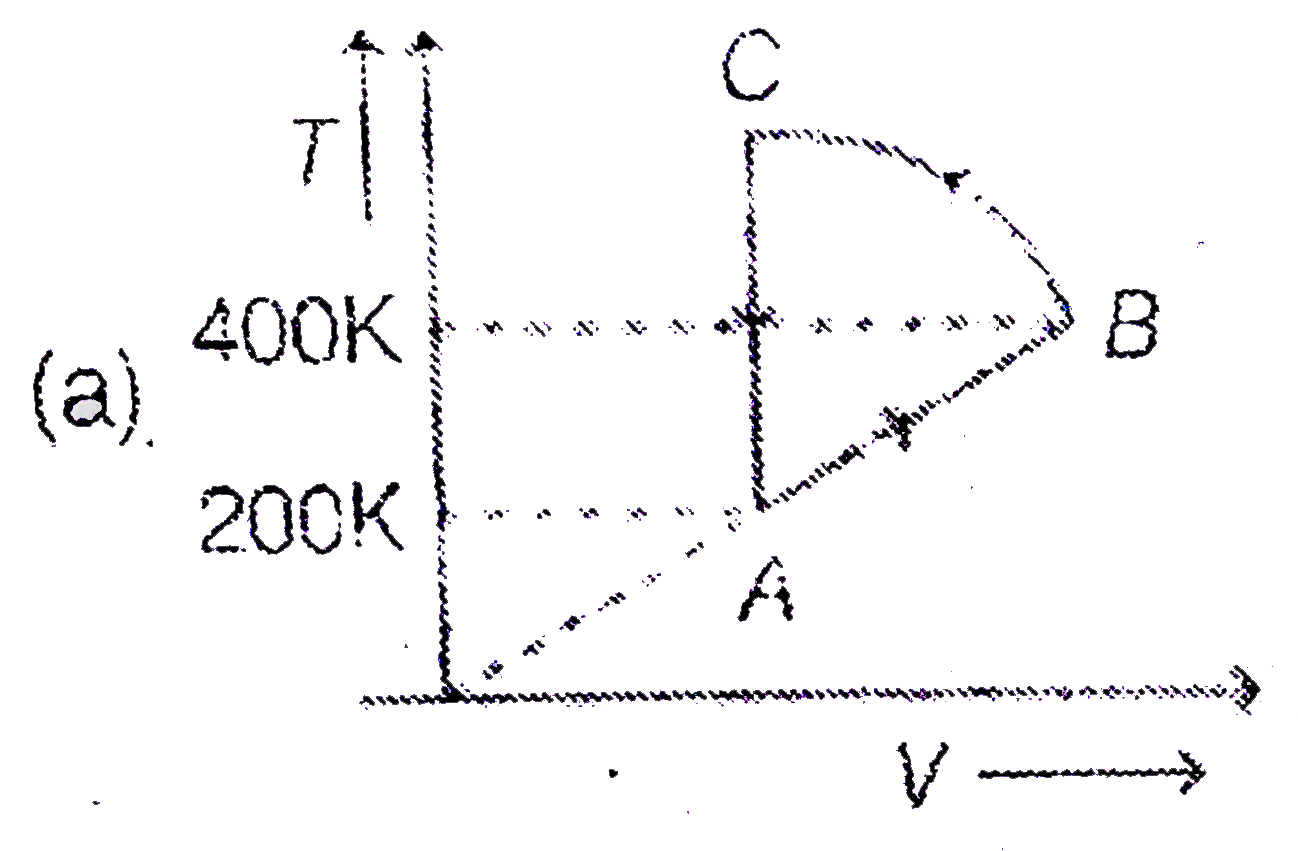

The correct Answer is:C
To solve the problem step by step, we will analyze the states of the gas and the relationships between pressure, volume, and temperature during the cyclic process.
Step 1: Identify the initial conditions
- The gas has 4 moles (n = 4).
- Initial pressure (P_A) = 2×105N/m2
- Initial temperature (T_A) = 200 K
Step 2: Determine the volume at state A
Using the ideal gas law, PV=nRT:
VA=nRTAPA
Substituting the values:
VA=4×8.3×2002×105
Calculating:
VA=6640200000=0.0332m3
Step 3: Determine the state B conditions
At state B, the pressure remains constant, and the temperature is increased to 400 K. Since pressure is constant:
VB=nRTBPA
Substituting the values:
VB=4×8.3×4002×105
Calculating:
VB=13280200000=0.0664m3
Step 4: Analyze the transition from state B to state C
From state B to state C, the temperature increases while the volume decreases. The volume at state C is equal to the volume at state A (i.e., VC=VA).
Step 5: Determine the conditions at state C
Since VC=VA, we have:
VC=0.0332m3
We need to find the temperature at state C (T_C). Using the ideal gas law again:
PBVC=nRTC
Substituting the values:
2×105×0.0332=4×8.3×TC
Calculating:
6666=33.2TC⟹TC=666633.2≈200K
Step 6: Analyze the final state A conditions
At state A, the gas is kept at constant volume and a total of 1000 J of heat is rejected. The process is cyclic, so the net heat exchange must equal zero.
Step 7: Determine the graph between T and V
- From A to B: T increases while V increases (straight line).
- From B to C: T increases while V decreases (curve).
- From C back to A: T remains constant while V is constant (horizontal line).
Conclusion
The correct graph will show:
- An initial increase in temperature with increasing volume from A to B.
- A decrease in volume with an increase in temperature from B to C.
- A constant temperature at state A.
- The gas has 4 moles (n = 4).
- Initial pressure (P_A) = 2×105N/m2
- Initial temperature (T_A) = 200 K
Using the ideal gas law, PV=nRT:
VA=nRTAPA
Substituting the values:
VA=4×8.3×2002×105
Calculating:
VA=6640200000=0.0332m3
At state B, the pressure remains constant, and the temperature is increased to 400 K. Since pressure is constant:
VB=nRTBPA
Substituting the values:
VB=4×8.3×4002×105
Calculating:
VB=13280200000=0.0664m3
From state B to state C, the temperature increases while the volume decreases. The volume at state C is equal to the volume at state A (i.e., VC=VA).
Since VC=VA, we have:
VC=0.0332m3
We need to find the temperature at state C (T_C). Using the ideal gas law again:
PBVC=nRTC
Substituting the values:
2×105×0.0332=4×8.3×TC
Calculating:
6666=33.2TC⟹TC=666633.2≈200K
At state A, the gas is kept at constant volume and a total of 1000 J of heat is rejected. The process is cyclic, so the net heat exchange must equal zero.
- From A to B: T increases while V increases (straight line).
- From B to C: T increases while V decreases (curve).
- From C back to A: T remains constant while V is constant (horizontal line).
The correct graph will show:
- An initial increase in temperature with increasing volume from A to B.
- A decrease in volume with an increase in temperature from B to C.
- A constant temperature at state A.
Topper's Solved these Questions
Similar Questions
Four moles of an ideal gas is initially in a state A having pressure 2×105N/m2 and temperature 200 K . Keeping pressure constant the gas is taken to state B at temperature of 400K. The gas is then taken to a state C in such a way that its temperature increases and volume decreases. Also from B to C, the magnitude of dTdV increases. The volume of gas at state C is eaual to its volume at state A. Now gas is taken is initial state A keeping volume constant. A total of 1000 J heat is rejected from the sample in the cyclic process. Take R=8.3J/K/mol.
The work done by the gas along path B to C is
View SolutionFour moles of an ideal gas is initially in state A having pressure 2×105N/m2 and temperature 200K . Keeping the pressure constant the gas is taken to state B at temperature of 400K. The gas is then taken to a state C in such a way that its temperature increases and volume decreases. Also from B to C , the magnitude of dT/dV increases. The volume of gas at state C is equal to its volume at state A. Now gas is taken to initial state A keeping volume constant. A total 1000J of heat is withdrawn from the sample of the cyclic process . Take R=8.3J/K/mol. The volume of gas at state C is
View Solution
Knowledge Check
What is the effect on the pressure of a gas if its temperature is increased at constant volume ?
AThe pressure of the gas increases.BThe pressure of the gas decreases .CThe pressure of the gas remains same .DThe pressure of the gas becomes half.
One mole of an ideal monoatomic gas is taken at a temperature of 300K. Its volume is doubled keeping its pressure constant. Find the change in internal energy.
View SolutionCan the temperature of a gas increased keeping its pressure and volume constant ?
View SolutionThe temperature of a given mass of a gas is increased from 19∘C to 20∘C at constant pressure. The volume V of the gas is
View SolutionA sample of ideal gas is taken through the cyclic process shown in the figure. The temerauture of the gas in state A is TA =200 K. In states B and C the temperature of the gas is the same.
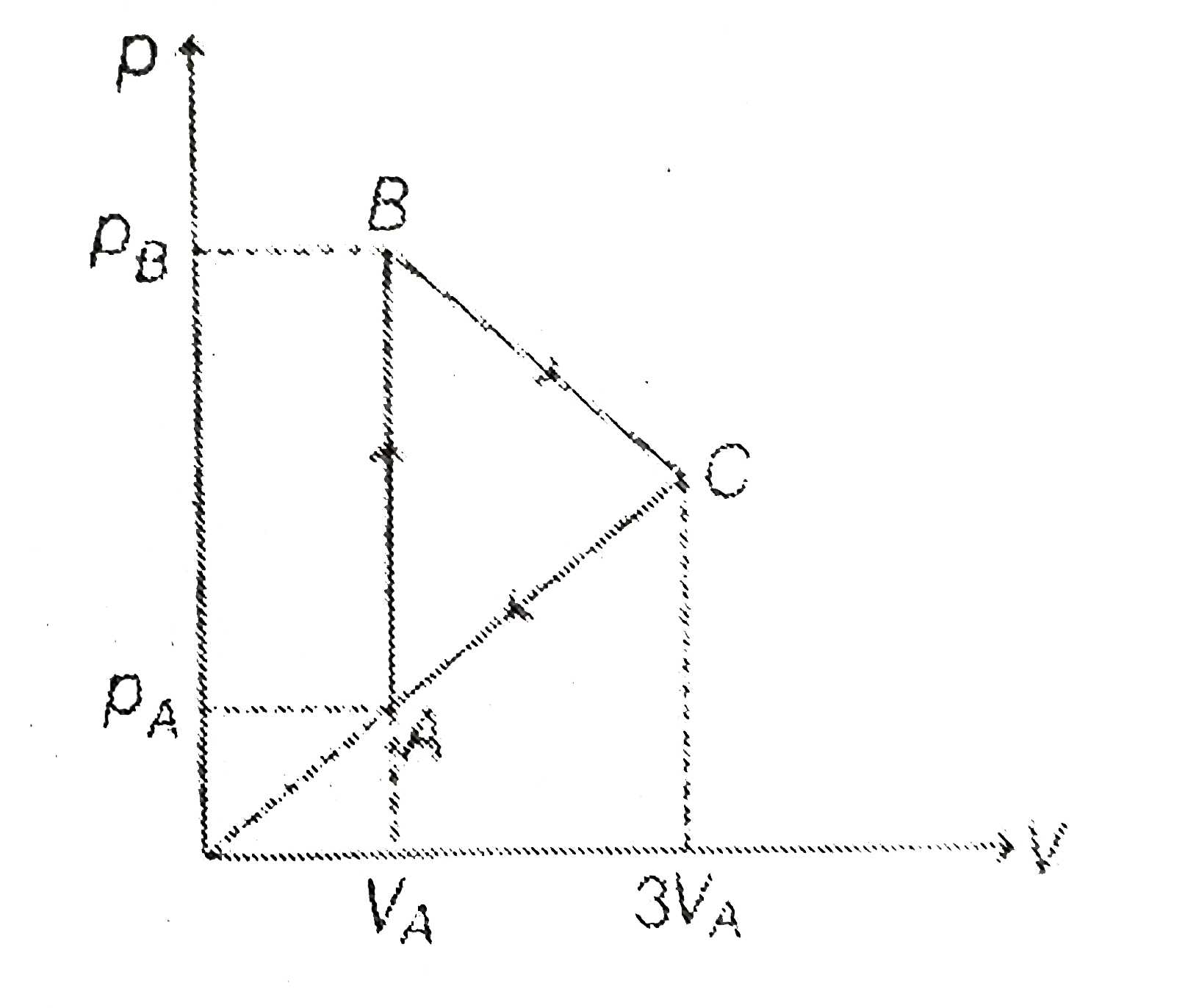
Net work done by the gas in the process is
View SolutionAt constant pressure, the ratio of increases in volume of an ideal gas per degree rise in kelvin temperature to its volume is
View SolutionFour moles of an ideal gas at a pressure of 4 atm and at a temperature of 70∘C expands is othermally to four times its initial volume : What is (i) the final temperature and (ii) the final volume ?
View SolutionA vessel is filled with an ideal gas at a pressure of 20atm and is a temperature of 27∘C One - half of the mass is removed from the vessel and the temperature of the remaining gas is increased to 87∘C. At this temperature, Find the pressure of the gas.
View Solution
