Vertical displacement of a plank with a body of mass m on it is varying according to the law y=sinωt+√3cosωt. The minimum value of ω for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).
√g2,√26,π√g
g√2,23√πg)
√g2,π3)√2g
√2g,√2π3g
The correct Answer is:A
To solve the problem, we need to analyze the motion of the plank and the mass on it, which is undergoing simple harmonic motion (SHM). The displacement of the plank is given by the equation:
y=sin(ωt)+√3cos(ωt)
1. Identify the Equation of Motion:
The vertical displacement of the plank is given by:
y=sin(ωt)+√3cos(ωt)
2. Convert to Standard Form:
We can express this equation in the standard form of SHM, y=Asin(ωt+ϕ). To do this, we can find the amplitude A and the phase ϕ:
A=√12+(√3)2=√1+3=√4=2
The angle ϕ can be found using:
tan(ϕ)=√31⟹ϕ=π3
Thus, we can rewrite the equation as:
y=2sin(ωt+π3)
3. Determine the Condition for Breaking Off:
The mass m will just break off the plank when the normal force N becomes zero. The forces acting on the mass are:
- Gravitational force: mg (downward)
- Normal force: N (upward)
When the mass just breaks off, we have:
mg=m⋅a
where a is the acceleration of the plank. The acceleration in SHM is given by:
a=−ω2y
Therefore, at the point of breaking off:
mg=m(−ω2y)
Simplifying gives:
g=−ω2y
4. Finding Minimum Value of ω:
For the mass to just break off, we need to find the maximum value of y, which is the amplitude A=2:
g=ω2A
Substituting A=2:
g=ω2⋅2⟹ω2=g2
Thus, the minimum value of ω is:
ω=√g2
5. Calculate the Time t When the Mass Breaks Off:
We need to find the time t when the mass first breaks off. We know that this occurs when:
y=2⟹2=2sin(ωt+π3)
This simplifies to:
1=sin(ωt+π3)
The first solution for sin(x)=1 is:
x=π2
Therefore:
ωt+π3=π2
Rearranging gives:
ωt=π2−π3=3π−2π6=π6
Thus:
t=π6ω
Final Answers:
- The minimum value of ω is:
ω=√g2
- The time t when the mass breaks off is:
t=π6ω
The vertical displacement of the plank is given by:
y=sin(ωt)+√3cos(ωt)
We can express this equation in the standard form of SHM, y=Asin(ωt+ϕ). To do this, we can find the amplitude A and the phase ϕ:
A=√12+(√3)2=√1+3=√4=2
The angle ϕ can be found using:
tan(ϕ)=√31⟹ϕ=π3
Thus, we can rewrite the equation as:
y=2sin(ωt+π3)
The mass m will just break off the plank when the normal force N becomes zero. The forces acting on the mass are:
- Gravitational force: mg (downward)
- Normal force: N (upward)
mg=m⋅a
where a is the acceleration of the plank. The acceleration in SHM is given by:
a=−ω2y
Therefore, at the point of breaking off:
mg=m(−ω2y)
Simplifying gives:
g=−ω2y
For the mass to just break off, we need to find the maximum value of y, which is the amplitude A=2:
g=ω2A
Substituting A=2:
g=ω2⋅2⟹ω2=g2
Thus, the minimum value of ω is:
ω=√g2
We need to find the time t when the mass first breaks off. We know that this occurs when:
y=2⟹2=2sin(ωt+π3)
This simplifies to:
1=sin(ωt+π3)
The first solution for sin(x)=1 is:
x=π2
Therefore:
ωt+π3=π2
Rearranging gives:
ωt=π2−π3=3π−2π6=π6
Thus:
t=π6ω
- The minimum value of ω is:
ω=√g2
- The time t when the mass breaks off is:
t=π6ω
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension types
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Only one question is correct
48 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A particle of mass 'm' is moving in the x−y plane such that its x and y coordinate vary according to the law x=asinωt and y=acosωt where 'a' and 'ω' are positive constants and 't' is time. Find
(a) equation of the path. Name the trajectory (path)
(b) whether the particle moves in clockwise or anticlockwise direction
magnitude of the force on the particle at any time t.
View SolutionA horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l0, to a point O. The coefficient of friciton between the bar and the plank is equal to m. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle θ.
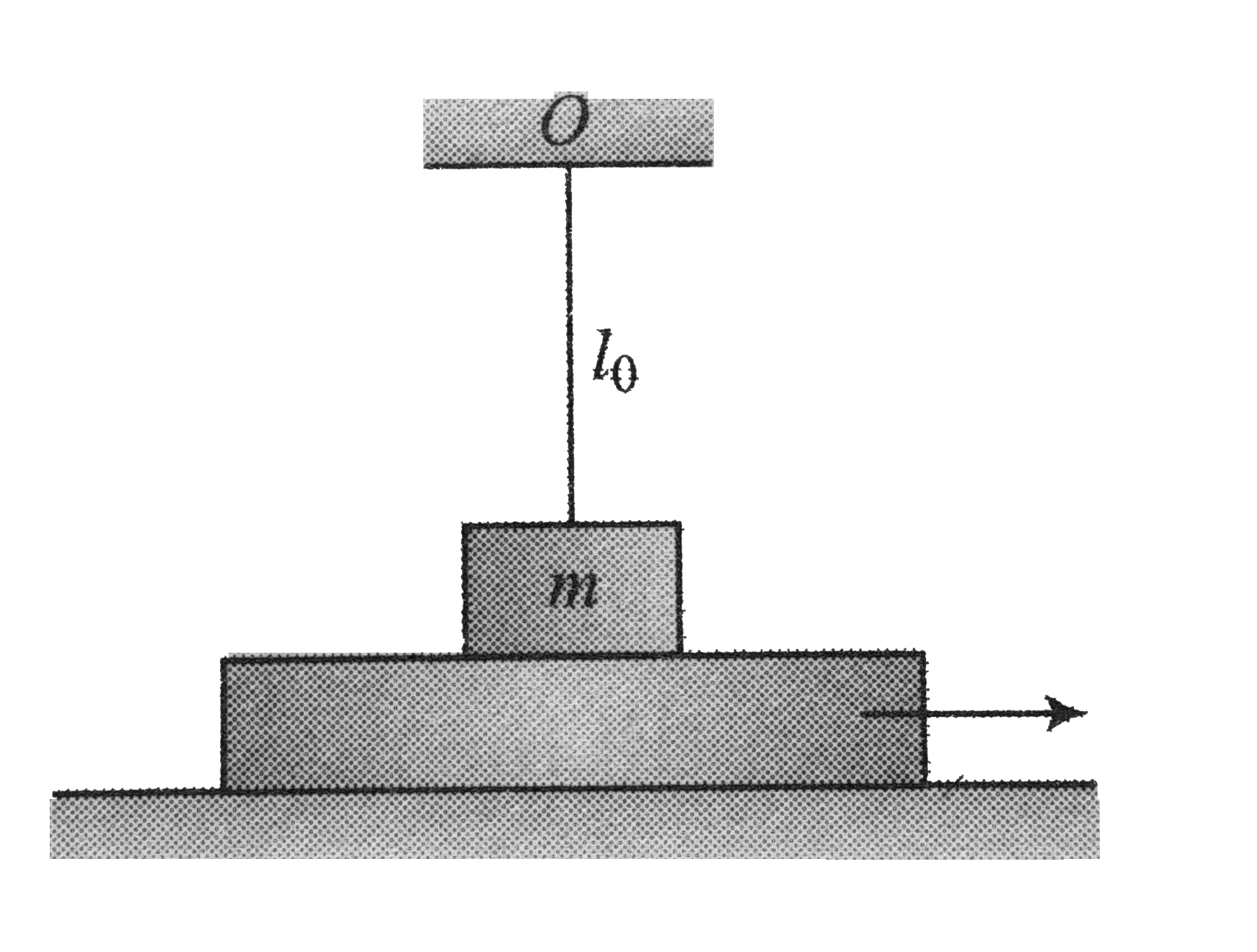
Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
View SolutionA particle of mass 'm' is moving in the x-y plane such that its x and y coordinate vary according to the law x= a sin ωt and y= a cos ωt where 'a' and 'omega' are positive constants and 't' is time. Find
(a) equation of the path. Name the trajectory (path).
(b) whether the particle moves in clockwise or anticlockwise direction
(c) magnitude of the force on the particle at any time t.
View SolutionA plank with a body of mass m placed on it starts moving straight up according to the law y=a(1−cosωt), where y is the displacement from the initial position, ω=11rad/s. Find
(a) The time independence of the force that the body exerts on the plank.
(b) The minimum amplitude of oscillations of the plank at which the body starts falling behind the plank.
View SolutionThe position of a particle moving along x-axis varies with time t according to equation x=√3sinωt−cosωt where ω is constants. Find the region in which the particle is confined.
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Find intantaneous power developed by electric force acting on the ring at t=1s
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
The magnitude of an electric field on the circumference of the ring is
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
Angular acceleration of ring is
View SolutionA thin non conducting ring of mass m, radius a carrying a charge q can rotate freely about its own axis which is vertical. At the initial moment, the ring was at rest in horizontal position and no magnetic field was present. At instant t=0, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law B=B0t. Neglecting magnetism induced due to rotational motion of ring.
The magnitude of induced emf of the closed surface of ring will be
View SolutionA locomotive of mass m starts moving so that its velocity varies according to the law v=a√s, where a is a constant, and s is the distance covered. Find the total work performed by all the forces which are acting on the locomotive during the first t seconds after the beginning of motion.
View Solution
