In hydrogen and hydrogen-like atom , the ratio of E4n−E2nandE2n−En varies with atomic nimber z and principal quantum numbern as
Z2N2
Z4n4
Zn
None of these
The correct Answer is:D
To solve the problem, we need to find the ratio of E4n−E2n and E2n−En for hydrogen and hydrogen-like atoms. The energy levels of hydrogen-like atoms are given by the formula:
En=−E1n2
where E1 is the energy of the ground state.
Step 1: Calculate E4n, E2n, and En
Using the formula for energy levels:
- For n=4n:
E4n=−E1(4n)2=−E116n2
- For n=2n:
E2n=−E1(2n)2=−E14n2
- For n=n:
En=−E1n2
Step 2: Compute E4n−E2n
Now we can find E4n−E2n:
E4n−E2n=(−E116n2)−(−E14n2)
This simplifies to:
E4n−E2n=−E116n2+E14n2
Finding a common denominator (which is 16n2):
E4n−E2n=−E116n2+4E116n2=3E116n2
Step 3: Compute E2n−En
Next, we calculate E2n−En:
E2n−En=(−E14n2)−(−E1n2)
This simplifies to:
E2n−En=−E14n2+E1n2
Finding a common denominator (which is 4n2):
E2n−En=−E14n2+4E14n2=3E14n2
Step 4: Calculate the ratio
Now we can find the ratio:
E4n−E2nE2n−En=3E116n23E14n2
The 3E1 and n2 terms cancel out:
E4n−E2nE2n−En=1/161/4=116×41=416=14
Conclusion
The ratio E4n−E2nE2n−En is a constant value of 14, which does not depend on the atomic number Z or the principal quantum number n. Therefore, the correct answer is:
Option D: None of this, that is no relation between z and n.
E4n=−E1(4n)2=−E116n2
E2n=−E1(2n)2=−E14n2
En=−E1n2
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (only one option is Correct)
76 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
Statement-1 : The excitation energy of He+ in its first excited state is 4 times the excitation energy of H in its first excited state.
Statement-2 : The whose energies are defined by the expansion E=−E0Z2n2 are stable, where Z and n are atomic number of the atom and principal quantum number of the orbit, respectively.
View SolutionAn electron in a hydrogen atom makes a transition n1→n2, where n1andn2 are principal quantum numbers of the states. Assume the Bohr's model to be valid. The time period of the electron in the initial state is eight times to that of final state. What is ratio of n2/n1
View Solution
Knowledge Check
The electron in hydrogen atom makes a transition n1→n2 where n1 and n2 are the principal quantum number of two states. Assuming the Bohr model to be valid, the time period of the electron in the initial state is eight times that in the final state. The possible value of n1 and n2 are:
An1=4,n2=2Bn1=8,n2=2Cn1=8,n2=1Dn1=6,n2=2
According to Bohr's theory, the time averaged magnetic field at the centre (i.e. nucleus) of a hydrogen atom due to the motion of electrons in the nth orbit is proportional to :
(n = principal quantum number)
View SolutionHydrogen atom:
The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as
En=−RHZ2n2 where RH=Rydberg constant,n=principal quantum number
What is the principal quantum number, n' of the orbit of Be3 that has the same Bohr radius as that of ground state hydrogen atom ?

View SolutionIn a hydrogen like atom electron make transition from an energy level with quantum number n to another with quantum number (n−1) if n>>1 , the frequency of radiation emitted is proportional to :
View SolutionIn Column I physical quantities corresponding to hydrogen and hydrogen like atom are given. In column II, powers of principal quantum number n are givem on which thosee physical quantities depend. Match the two columns.
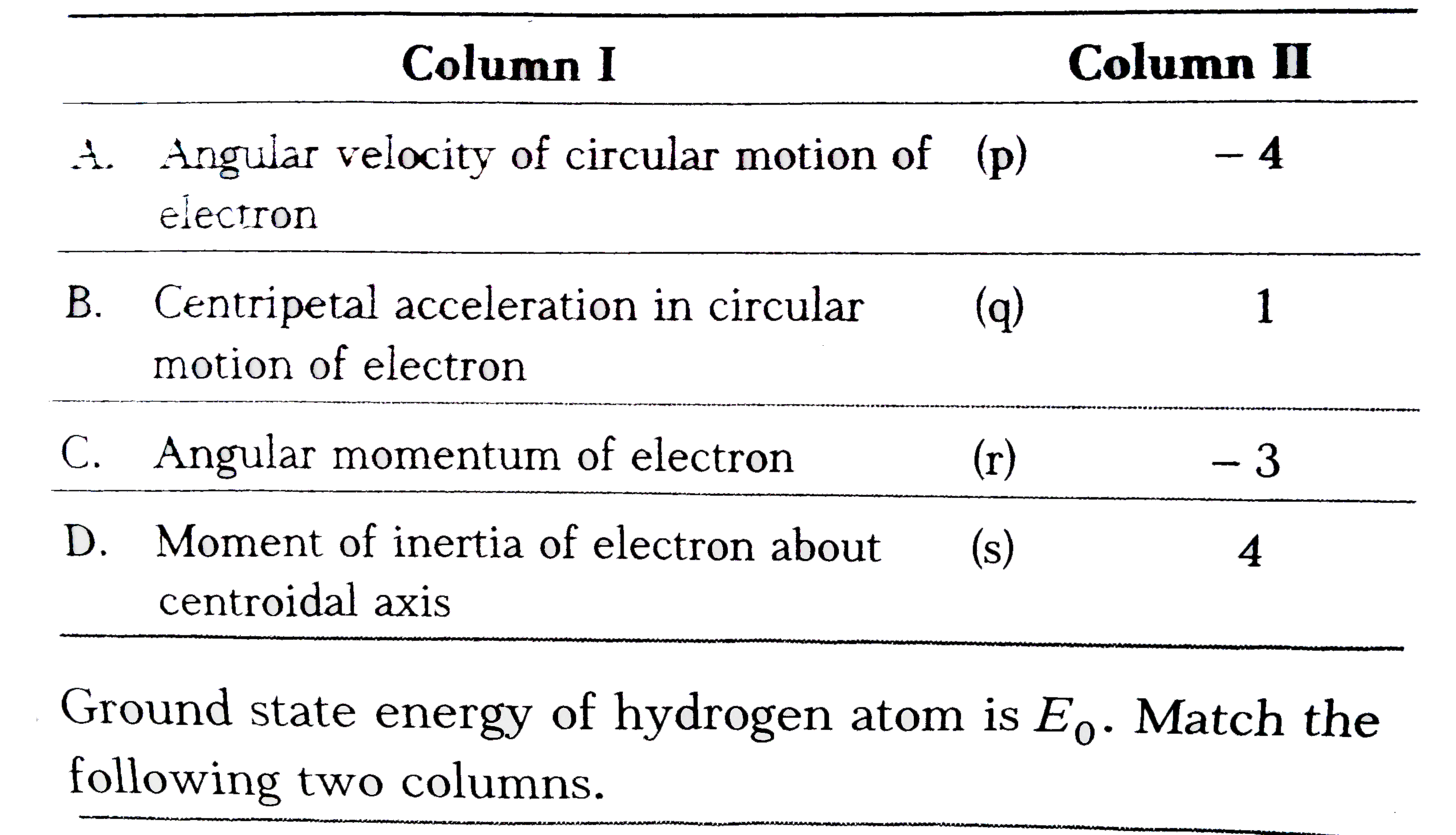
View SolutionHydrogen atom:
The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as
En=−RHZ2n2 where RH=Rydberg constant,n=principal quantum number
The energy in Joule of an electron in the second orbit of H- atom is:
View SolutionHydrogen atom:
The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as
En=−RHZ2n2 where RH=Rydberg constant,n=principal quantum number
Calculate the following :
(a) the kinetic energy (in eV) of an electron in the ground state of hydrogen atom.
(b) the potential energy (in eV) of an electron in the ground state of hydrogen atom.
View SolutionHydrogen atom:
The electronic ground state of hydrogen atom contains one electron in the first orbit. If sufficient energy is provided, this electron can be promoted to higher energy levels. The electronic energy of a hydrogen-like species (any atom//ions with nuclear charge Z and one electron) can be given as
En=−RHZ2n2 where RH=Rydberg constant,n=principal quantum number
The ratio of energy of an electron in the ground state Be3− ion to that of ground state H atom is:
The kinetic and potential energies of an electron in the H atoms are given as
K.E.=e24πε02r and P.E.=−14πε0e2r
View Solution
