In a hypothetical system , a partical of mass and charge is moving around a very heavy partical chaRGE . Assume that Bohr's model is applicable to this system , then velocuity of mass in the first orbit is
The correct Answer is:A
To find the velocity of a particle of mass m and charge −3q moving around a very heavy particle with charge q in the first orbit, we can use the principles derived from Bohr's model of the atom.
1. Understanding the System:
We have a particle with charge −3q moving in a circular orbit around a heavy particle with charge q. According to Coulomb's law, the electrostatic force provides the necessary centripetal force for circular motion.
2. Centripetal Force and Electrostatic Force:
The electrostatic force F between the two charges is given by:
F=k⋅|q1⋅q2|r2=k⋅|(−3q)⋅q|r2=3kq2r2
where k is Coulomb's constant and r is the radius of the orbit.
3. Centripetal Force Requirement:
The centripetal force required to keep the particle in circular motion is given by:
Fc=mv2r
where m is the mass of the particle and v is its velocity.
4. Setting Forces Equal:
For the particle to maintain its circular motion, the centripetal force must equal the electrostatic force:
mv2r=3kq2r2
5. Rearranging the Equation:
We can rearrange this equation to find v2:
mv2=3kq2r
v2=3kq2mr
6. Using Bohr's Quantization Condition:
According to Bohr's model, the angular momentum L is quantized:
L=nh2π
For the first orbit, n=1:
L=h2π
The angular momentum can also be expressed as:
L=mvr
Setting these equal gives:
mvr=h2π
From this, we can express v:
v=h2πmr
7. Substituting v into the Force Equation:
Now, substitute v back into the equation for v2:
(h2πmr)2=3kq2mr
Simplifying gives:
h24π2m2r2=3kq2mr
Multiplying both sides by 4π2m2r2:
h2=12π2kq2mr
8. Solving for v:
Now we can solve for v using the relationship we derived earlier:
v=√3kq2mr
Substituting r from the angular momentum equation gives us the final expression for the velocity.
Final Expression:
After simplifying, we find:
v=3q22πϵ0h
Conclusion:
The velocity of the particle in the first orbit is given by:
v=3q22πϵ0h
We have a particle with charge −3q moving in a circular orbit around a heavy particle with charge q. According to Coulomb's law, the electrostatic force provides the necessary centripetal force for circular motion.
The electrostatic force F between the two charges is given by:
F=k⋅|q1⋅q2|r2=k⋅|(−3q)⋅q|r2=3kq2r2
where k is Coulomb's constant and r is the radius of the orbit.
The centripetal force required to keep the particle in circular motion is given by:
Fc=mv2r
where m is the mass of the particle and v is its velocity.
For the particle to maintain its circular motion, the centripetal force must equal the electrostatic force:
mv2r=3kq2r2
We can rearrange this equation to find v2:
mv2=3kq2r
v2=3kq2mr
According to Bohr's model, the angular momentum L is quantized:
L=nh2π
For the first orbit, n=1:
L=h2π
The angular momentum can also be expressed as:
L=mvr
Setting these equal gives:
mvr=h2π
From this, we can express v:
v=h2πmr
Now, substitute v back into the equation for v2:
(h2πmr)2=3kq2mr
Simplifying gives:
h24π2m2r2=3kq2mr
Multiplying both sides by 4π2m2r2:
h2=12π2kq2mr
Now we can solve for v using the relationship we derived earlier:
v=√3kq2mr
Substituting r from the angular momentum equation gives us the final expression for the velocity.
After simplifying, we find:
v=3q22πϵ0h
The velocity of the particle in the first orbit is given by:
v=3q22πϵ0h
Topper's Solved these Questions
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - for JEE Advanced (More than One Options is Correct )
1 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Metch the column
6 Videos
- MODERN PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICSEXERCISE - Integer Type Questions
17 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
- MODERN PHYSICS - 1BOOK - DC PANDEY ENGLISHCHAPTER - MODERN PHYSICS - 1EXERCISE - Level 2 Subjective
23 Videos
Similar Questions
A particle of mass m carrying charge '+q1' is revolving around a fixed charge '−q2' in a circular path of radius r. Calculate the period of revolution.
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA particle of mass m and charge -q circulates around a fixed charge q in a circle radius under electrostatic force. The total energy of the system is (k= (14πε0))
View SolutionA particle known as mu meson has a charge equal to that of no electron and mass 208times the mass of the electron B moves in a circular orbit around a nucleus of charge +3e Take the mass of the nucleus to be infinite Assuming that the bohr's model is applicable to this system (a)drive an expression for the radius of the nth Bohr orbit (b) find the value of a for which the radius of the orbit it appropriately the same as that at the first bohr for a hydrogen atom (c) find the wavelength of the radiation emitted when the u - mean jump from the orbit to the first orbit
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionAn imaginary particle has a charge equal to that of an electron and mass 100 times tha mass of the electron. It moves in a circular orbit around a nucleus of charge + 4 e. Take the mass of the nucleus to be infinite. Assuming that the Bhor model is applicable to this system. (a)Derive an experssion for the radius of nth Bhor orbit. (b) Find the wavelength of the radiation emitted when the particle jumps from fourth orbit to the second orbit.
View SolutionA particle of mass m and charge q is thrown in a region where uniform gravitational field and electric field are present. The path of particle:
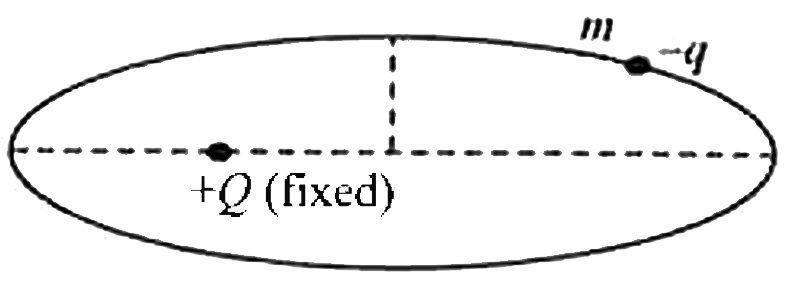
View SolutionA positive point charge +Q is fixed in space. A negative point charge −q of mass m revolves around fixed charge in elliptical orbit. The fixed charge +Q is at one focus of the ellipse. The only force acting on negative charge is the electrostic force due to positive charge. Then which of the following statement is true
View SolutionMass centers of a system of three particles of masses 1,2,3kg is at the point (1m,2m,3m) and mass center of another group of two partices of masses 2kg and 3kg is at point (−1m,3m,−2m). Where a 5kg particle should be placed, so that mass center of the system of all these six particles shifts to mass center of the first system?
View SolutionAn electron is moving around infinite linear positive charge in the orbit of 0.1 m. If the linear charge density is 1μC/m, the velocity of electron will be
View Solution
