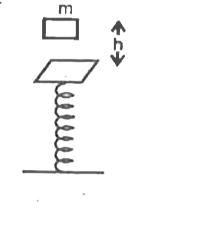
A body of mass m is released from a height h to a scale pan hung from a spring. The spring constant of the spring is k, the mass of the scale pan is negligible and the body does not bounce relative to the pan, then the amplitude of vibration is
mg
mgk√1+2hkmg
mgk+mgk√1+2hkmg
None of the above
The correct Answer is:B
To solve the problem step by step, we will analyze the situation involving a mass m released from a height h onto a spring with spring constant k.
Step 1: Understand the System
The body of mass m is released from a height h and falls onto a spring. The spring will compress when the mass lands on it, and we need to find the maximum compression of the spring, which will correspond to the amplitude of vibration.
Step 2: Energy Conservation
We will use the principle of conservation of mechanical energy. The total mechanical energy at the height h (potential energy) will be equal to the total mechanical energy when the spring is at maximum compression (potential energy in the spring).
1. Potential Energy at Height h:
\(
PE_{\text{initial}} = mgh
\)
2. Potential Energy in the Spring at Maximum Compression:
When the spring is compressed by a distance y, the potential energy stored in the spring is given by:
\(
PE_{\text{spring}} = \frac{1}{2}ky^2
\)
Step 3: Set Up the Energy Conservation Equation
At the point of maximum compression, all the potential energy from the height will be converted into the potential energy of the spring:
\(
mgh = \frac{1}{2}ky^2
\)
Step 4: Rearranging the Equation
Rearranging the equation gives us:
\(
ky^2 = 2mgh
\)
\(
y^2 = \frac{2mgh}{k}
\)
Step 5: Solve for y
Taking the square root of both sides, we find:
\(
y = \sqrt{\frac{2mgh}{k}}
\)
Step 6: Identify the Amplitude
Since y represents the maximum compression of the spring, it is also the amplitude of the vibration. Therefore, the amplitude A is given by:
\(
A = y = \sqrt{\frac{2mgh}{k}}
\)
Final Answer
The amplitude of vibration is:
\(
A = \sqrt{\frac{2mgh}{k}}
\)
---
The body of mass m is released from a height h and falls onto a spring. The spring will compress when the mass lands on it, and we need to find the maximum compression of the spring, which will correspond to the amplitude of vibration.
We will use the principle of conservation of mechanical energy. The total mechanical energy at the height h (potential energy) will be equal to the total mechanical energy when the spring is at maximum compression (potential energy in the spring).
\(
PE_{\text{initial}} = mgh
\)
When the spring is compressed by a distance y, the potential energy stored in the spring is given by:
\(
PE_{\text{spring}} = \frac{1}{2}ky^2
\)
At the point of maximum compression, all the potential energy from the height will be converted into the potential energy of the spring:
\(
mgh = \frac{1}{2}ky^2
\)
Rearranging the equation gives us:
\(
ky^2 = 2mgh
\)
\(
y^2 = \frac{2mgh}{k}
\)
Taking the square root of both sides, we find:
\(
y = \sqrt{\frac{2mgh}{k}}
\)
Since y represents the maximum compression of the spring, it is also the amplitude of the vibration. Therefore, the amplitude A is given by:
\(
A = y = \sqrt{\frac{2mgh}{k}}
\)
The amplitude of vibration is:
\(
A = \sqrt{\frac{2mgh}{k}}
\)
Topper's Solved these Questions
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved Papers 2017(JIPMER)
28 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(NEET)
22 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SOUND WAVESBOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.7
4 Videos
Similar Questions
A block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
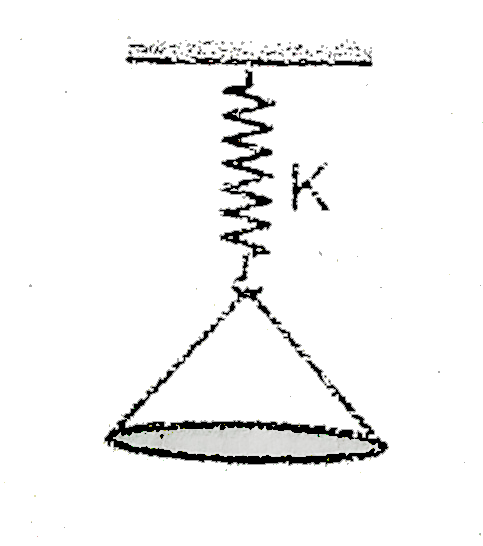
View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA body of mass m falls from a height h on a pan ( of negligible mass ) of spring balance as shwon. The spring is ideal and has a spring contant k. Just after striking the pan, the body sticks with the pan and starts oscillatory motion in vertical direction. The velocity of the body at mean position will be
View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
The largest amplitude Amax, for which the string will remain taut throughout the motion is
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution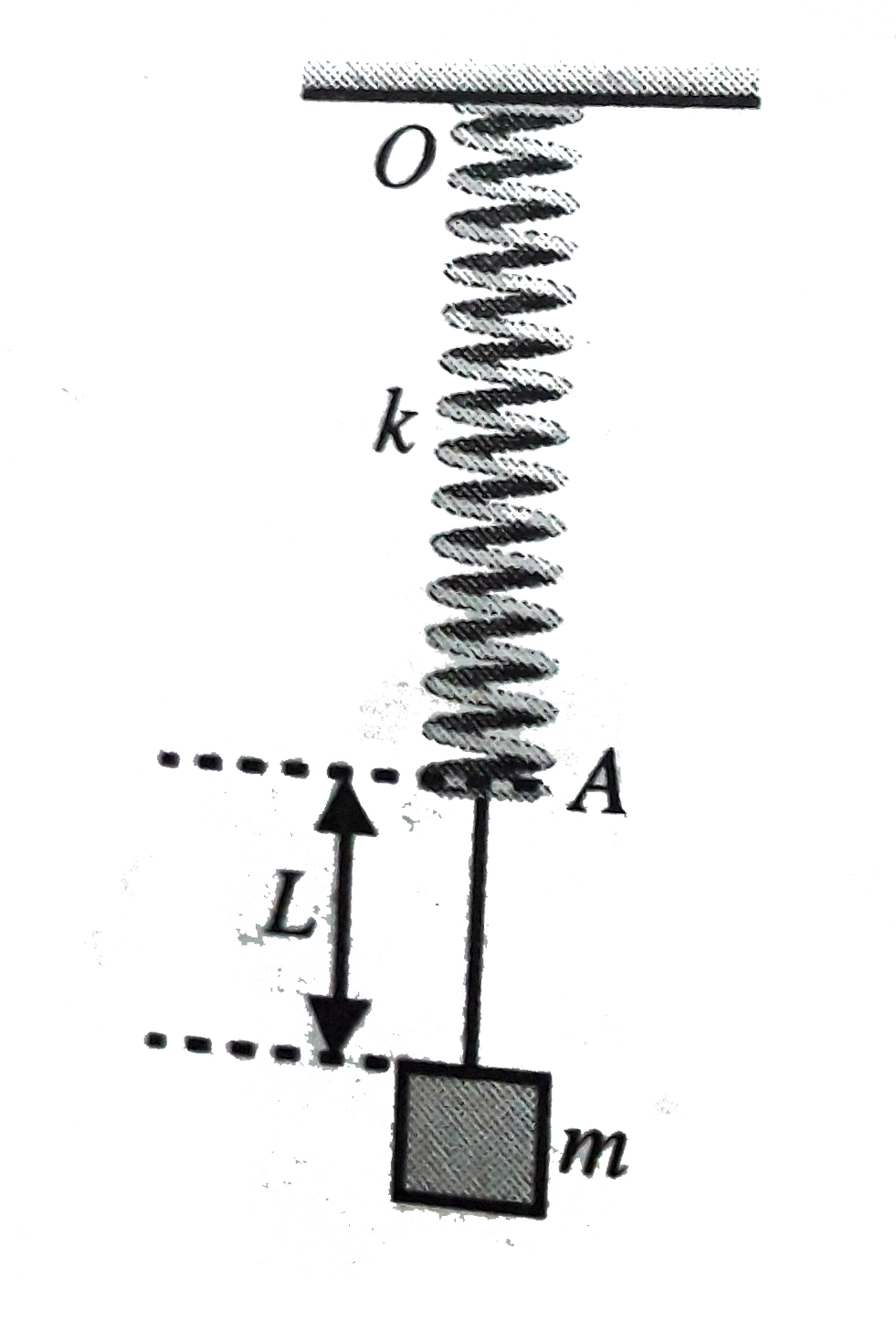
A body of mass m is attached by an inelastic string to a suspended spring of spring constant k. Both the string and the spring have negligible mass and the string is inextensible and of length L. Initially, the mass m is at rest.
Q. If the mass m is now raised up to point A (the top end of the string see fig. and allowed to fall from rest, the maximum extension of the spring in the subsequent motion will be
View SolutionA body of mass m suspended from an ideal spring is executing simple harmonic oscillations. The force constant of the spring is k and the time period of the body is T. Show by dimensional method that the formula T=2πm/k is incorrect. Establish its correct form.
View SolutionA ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View Solution
