The wheel of a car, accelerated uniformly from rest, rotates through 1.5 rad during the first second. Find the angle rotated during the next second.
To solve the problem step by step, we will follow the reasoning outlined in the video transcript.
Step 1: Understand the given information
We know that the wheel of a car starts from rest and rotates through an angle of 1.5 radians during the first second. We need to find the angle rotated during the next second.
Step 2: Identify the initial conditions
- Initial angular velocity, \( \omega_0 = 0 \) rad/s (since it starts from rest).
- Angular displacement during the first second, \( \theta_1 = 1.5 \) rad.
- Time for the first interval, \( t_1 = 1 \) s.
Step 3: Use the equation of motion for angular displacement
For uniformly accelerated motion, the angular displacement can be calculated using the formula:
\(
\theta = \omega_0 t + \frac{1}{2} \alpha t^2
\)
Since the initial angular velocity \( \omega_0 = 0 \), the equation simplifies to:
\(
\theta = \frac{1}{2} \alpha t^2
\)
Step 4: Substitute the known values for the first second
For the first second:
\(
1.5 = \frac{1}{2} \alpha (1^2)
\)
This simplifies to:
\(
1.5 = \frac{1}{2} \alpha
\)
Multiplying both sides by 2 gives:
\(
\alpha = 3 \text{ rad/s}^2
\)
Step 5: Calculate the angular displacement for the first two seconds
Now we need to find the total angular displacement after 2 seconds using the same formula:
\(
\theta = \frac{1}{2} \alpha t^2
\)
Substituting \( \alpha = 3 \) rad/s² and \( t = 2 \) s:
\(
\theta_2 = \frac{1}{2} \cdot 3 \cdot (2^2) = \frac{1}{2} \cdot 3 \cdot 4 = 6 \text{ radians}
\)
Step 6: Find the angle rotated during the next second
The angle rotated during the next second (from 1 second to 2 seconds) is given by:
\(
\text{Angle in the second second} = \theta_2 - \theta_1
\)
Substituting the values:
\(
\text{Angle in the second second} = 6 - 1.5 = 4.5 \text{ radians}
\)
Final Answer
The angle rotated during the next second is 4.5 radians.
---
We know that the wheel of a car starts from rest and rotates through an angle of 1.5 radians during the first second. We need to find the angle rotated during the next second.
- Initial angular velocity, \( \omega_0 = 0 \) rad/s (since it starts from rest).
- Angular displacement during the first second, \( \theta_1 = 1.5 \) rad.
- Time for the first interval, \( t_1 = 1 \) s.
For uniformly accelerated motion, the angular displacement can be calculated using the formula:
\(
\theta = \omega_0 t + \frac{1}{2} \alpha t^2
\)
Since the initial angular velocity \( \omega_0 = 0 \), the equation simplifies to:
\(
\theta = \frac{1}{2} \alpha t^2
\)
For the first second:
\(
1.5 = \frac{1}{2} \alpha (1^2)
\)
This simplifies to:
\(
1.5 = \frac{1}{2} \alpha
\)
Multiplying both sides by 2 gives:
\(
\alpha = 3 \text{ rad/s}^2
\)
Now we need to find the total angular displacement after 2 seconds using the same formula:
\(
\theta = \frac{1}{2} \alpha t^2
\)
Substituting \( \alpha = 3 \) rad/s² and \( t = 2 \) s:
\(
\theta_2 = \frac{1}{2} \cdot 3 \cdot (2^2) = \frac{1}{2} \cdot 3 \cdot 4 = 6 \text{ radians}
\)
The angle rotated during the next second (from 1 second to 2 seconds) is given by:
\(
\text{Angle in the second second} = \theta_2 - \theta_1
\)
Substituting the values:
\(
\text{Angle in the second second} = 6 - 1.5 = 4.5 \text{ radians}
\)
The angle rotated during the next second is 4.5 radians.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples2videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples5videos
CIRCULAR MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
The wheel of a motor, accelerated uniformly from rest, rotates through 2.5 radian during the first second. Find the angle rotated during the next second.
View SolutionA wheel initially at rest, is rotated with a uniform angular acceleration. The wheel rotates through an angleθ1 in first one second and through an additional angle θ2 in the next one second. The ratio θ2/θ1 is :
View SolutionA wheel initially at rest, is rotated with a uniform angular acceleration. The wheel rotates through an angle θ1 in the first one second and through an additional angle θ2 in the next one second. The ratio θ1/θ2 is:
View SolutionA wheel starting from rest is uniformly accelerate at 4 rads2 for 10 seconds. It is allowed to rotate uniformly for the next 10 seconds and is finally brought to rest in the next 10 seconds. Find the total angle rotated by the wheel.
View SolutionA wheel is making revolutions about its axis with uniform angular acceleration. Starting from rest, till it reaches 100 rev/sec in 4 seconds. Find the angular acceleration. Find the angle rotated during these four seconds.
View SolutionA body ,starting from rest and moving with constant acceleration,covers 10m in the first second.Find the distance travelled by it in the next second.
View SolutionA wheel which is initially at rest is subjected to a constant angular acceleration about its axis. It rotates through an angle of 15∘ in time t sec. Then how much it rotates in the next 2t sec
View SolutionA wheel starting from rest is uniformly accelerated at 4rad/s2 for 10s. It is allowed to rotated uniformly for the next 10 s and is finally brought to rest in the next 10 s. Find the total angle rotated by the wheel.
View SolutionThe speed of a car increases uniformly from zero to 10ms−1 in 2s and then remains constant (figure)
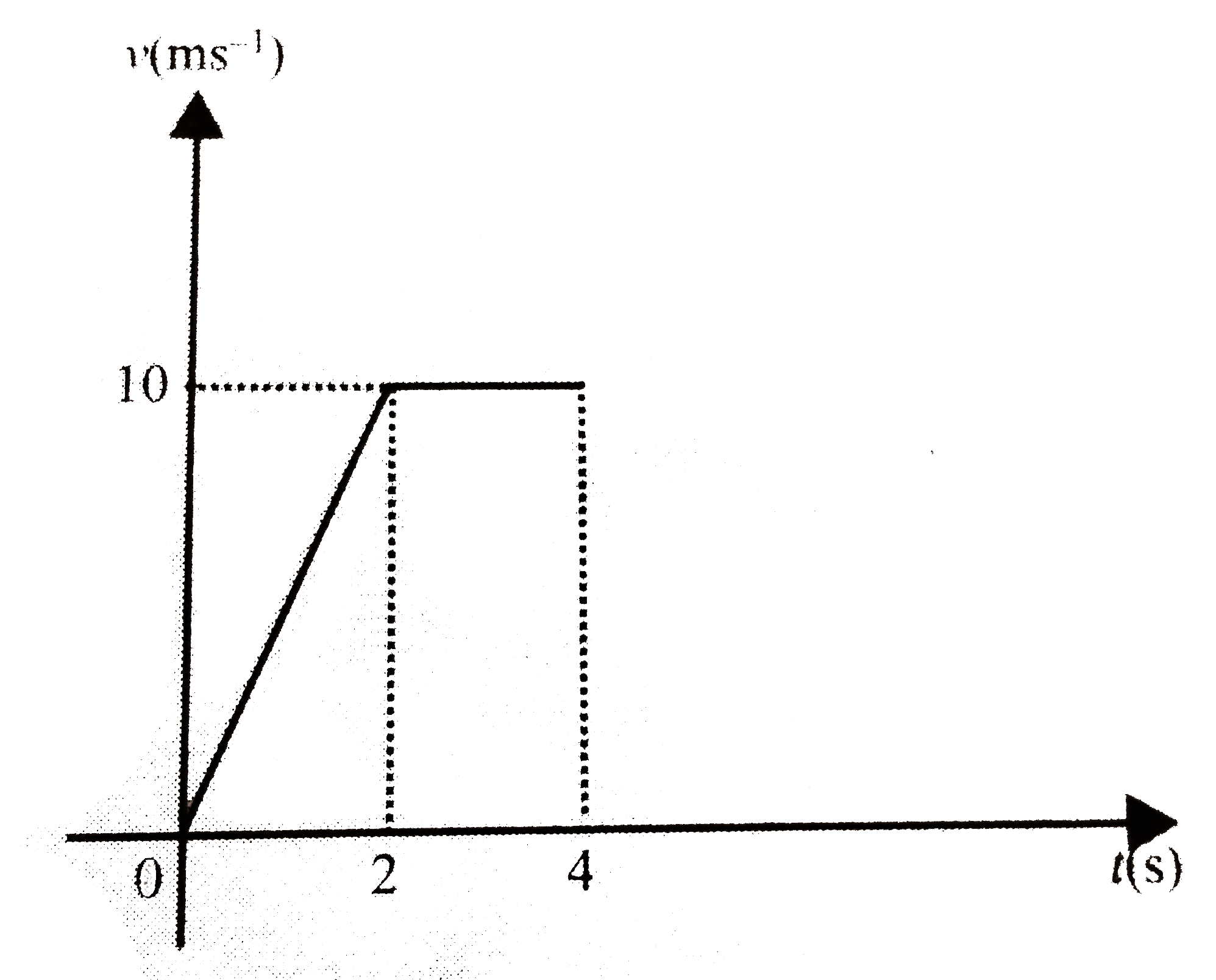
a. Find the distance travelled by the car in the first two seconds.
b. Find the distance travelled by the car in the next two seconds.
c. Find the total distance travelled in 4s.View SolutionA body starts from rest and accelerates with 4m/s2 for 5 seconds. Find the distance travelled with 5 seconds.
View Solution

